Relaciones métricas más importantes: Áreas y Perímetros: Cuadro

Relaciones métricas más importantes:
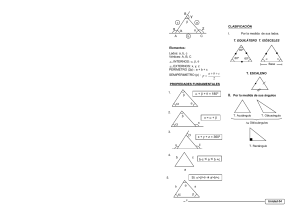
Áreas y Perímetros:
Cuadro resumen:
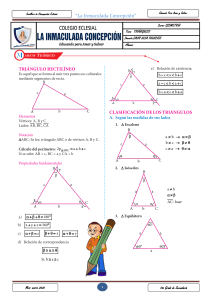
Deducción elemental del Teorema de Pitágoras.
EJERCICIOS DE APLICACIÓN:
1.-En las figuras , calcular el valor de cada incógnita que se indica:
5
18 , 9
4
6
3
5
8
12 , 12
X=30º ,
y=60º
X=30º ,
y=60º
X=60º
Z=30º
20
7,5 ;
7,5
X=30º
Y=60º
13 , 26
4
6 , 12
4
4 , 8
2.- Para cada una de las figuras anteriores, calcule el área y el perímetro.
6
96
2
88
24
18
4,5
-
32
72
8
42
192
16
18
0.78
0,03125
3.- En cada caso, compruebe que el triángulo que se indica es rectángulo:
4.- Calcule el perímetro y el área de cada un de los triángulos del ítem anterior.
30 , 30
360 , 4320
2+ +
72, 216
-
3+
, 1
,
20+6
24 , 24
36+18
, 60
10+2
9+
, 81
5.- Calcule el área sombreada que se indica.(considere π=3)
23+
, 10
36
18
33
144(
675
3
48+144
9
48-36
96
6.- Resuelva los problemas que se indican:
6.1.- Se tiene un triángulo equilátero de lado 12 3 .Se traza un arco con centro en uno de los
vértices y con radio equivalente a la altura del lado opuesto a este vértice .Calcular al área del
sector circular que se determina.
(54  cm 2 )
6.2.- Los catetos de un triángulo rectángulo miden 18 y 24 cm. respectivamente .Haciendo centro
en el vértice del ángulo recto y con radio equivalente a la altura a la hipotenusa se traza un arco
que genera un cuarto de círculo. Calcular la superficie del sector circular que se determina.
(51,84  cm 2 )
6.3.- El ángulo en el vértice B de un triángulo rectángulo en C, mide 30º .Si con centro en A y radio
equivalente a la altura a la hipotenusa (h) se traza un arco tangente a dicha hipotenusa .Calcular
la superficie del sector que se determina.
(h 2  /6)
6.4.- En un cuadrado de lado a, se traza un arco de círculo tomando uno de los vértices como
centro y el lado del cuadrado como radio. Calcular la superficie de una embecadura.
a 2 (4-  )/4