Función cuadrática - Facultad de Ciencias Naturales

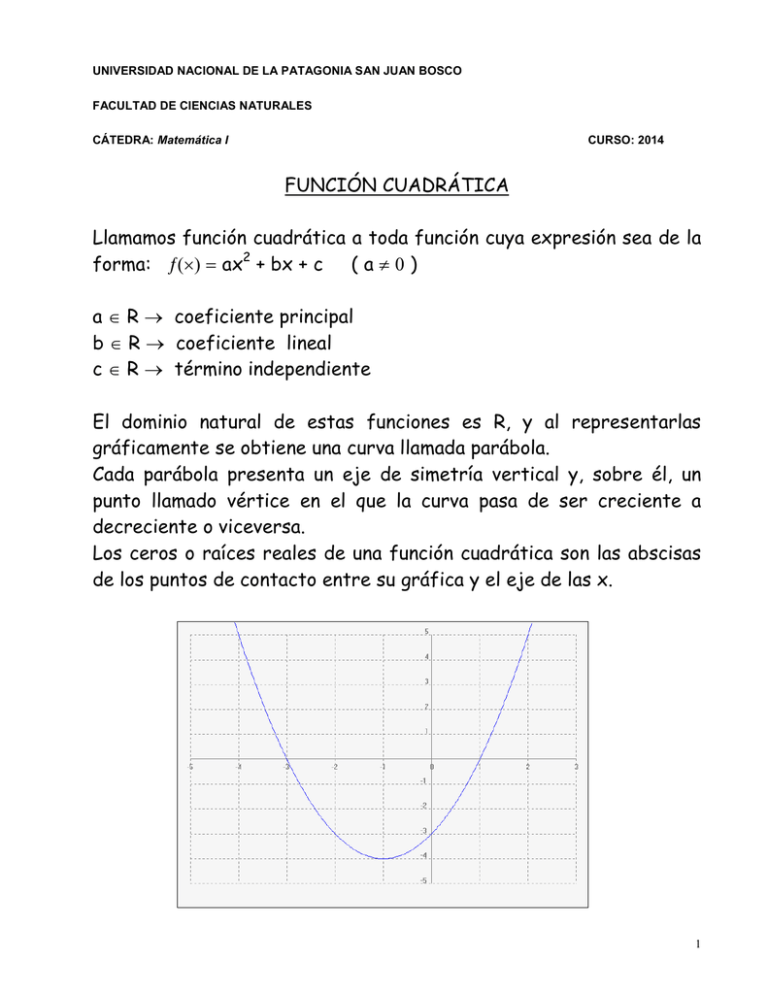
UNIVERSIDAD NACIONAL DE LA PATAGONIA SAN JUAN BOSCO
FACULTAD DE CIENCIAS NATURALES
CÁTEDRA: Matemática I
CURSO: 2014
FUNCIÓN CUADRÁTICA
Llamamos función cuadrática a toda función cuya expresión sea de la
forma: ƒ(×) = ax2 + bx + c ( a ≠ 0 )
a ∈ R → coeficiente principal
b ∈ R → coeficiente lineal
c ∈ R → término independiente
El dominio natural de estas funciones es R, y al representarlas
gráficamente se obtiene una curva llamada parábola.
Cada parábola presenta un eje de simetría vertical y, sobre él, un
punto llamado vértice en el que la curva pasa de ser creciente a
decreciente o viceversa.
Los ceros o raíces reales de una función cuadrática son las abscisas
de los puntos de contacto entre su gráfica y el eje de las x.
1
CONSTRUCCIÓN DE LA GRÁFICA DE
CUADRÁTICA.
Para graficar la función ƒ(×) = - x2 + 2x + 3
UNA
FUNCIÓN
• Hallamos sus raíces, haciendo ƒ(×) = 0 y resolviendo la ecuación de
segundo grado: - x2 + 2x + 3 = 0, en éste caso aplicando la fórmula
de Bhaskara reemplazando los coeficientes a, b y c en la siguiente
expresión:
x1,2 = -b + √ b2 – 4ac
⇒
x 1 = - 1 y x2 = 3
2a
• Calculamos la ecuación del eje de simetría, que pasa por la abscisa
del vértice, promediando las raíces (ya que equidistan del eje)
x = x 1 + x2
2
x = 1 → ecuación del eje
xv = 1 abscisa del vértice.
• Calculamos la ordenada del vértice:
yv = ƒ(×v) = -(1)2 + 2.(1) + 3 = 4
⇒ V = (1;4)
• Calculamos la ordenada al origen que es la imagen del 0, ƒ(0 )
(recuerden que es la ordenada del punto de intersección de la
curva con el eje de las ordenadas )
ƒ(0 ) = -(0)2 + 2.(0) + 3 = 3
Con los datos detallados anteriormente, ubicarlos en el siguiente
plano xy, y trazar el gráfico de la parábola.
2
DISTINTAS
FORMAS
DE
EXPRESAR
UNA
FUNCIÓN
CUADRÁTICA.
Si una función cuadrática tiene raíces reales x1 y x2, ya sean iguales o
distintas, su fórmula puede expresarse en forma factorizada, así:
ƒ(×) = ax2 + bx + c ⇒ ƒ(×) = a.( x – x1 ).(x – x2 )
Si conocemos las coordenadas del vértice de una función cuadrática,
su fórmula puede expresarse en forma canónica así:
ƒ(×) = a.( x – xv )2 + yv
xv = abscisa del vértice, yv = ordenada del vértice.
EN RESUMEN: En cada una de esas formas, figuran tres parámetros.
Forma
Expresión
Parámetros
Polinómica
ƒ(×) = ax2 + bx + c
a, b, c
Canónica
ƒ(×) = a.( x – xv )2 + yv
a, xv, yv
Factorizada
ƒ(×) = a.( x – x1 ).(x – x2 )
a, x1, x2
3