FUNCIONES CUADRÁTICAS A la función polinómica de segundo

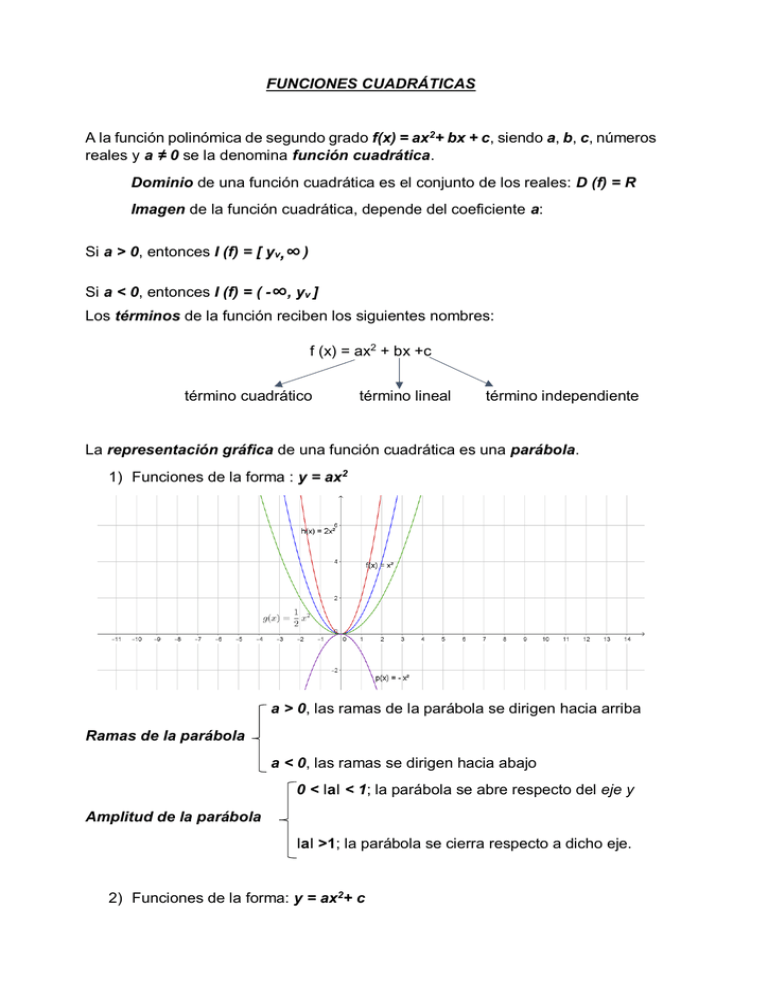
FUNCIONES CUADRÁTICAS
A la función polinómica de segundo grado f(x) = ax2+ bx + c, siendo a, b, c, números
reales y a ≠ 0 se la denomina función cuadrática.
Dominio de una función cuadrática es el conjunto de los reales: D (f) = R
Imagen de la función cuadrática, depende del coeficiente a:
Si a > 0, entonces I (f) = [ yv,∞ )
Si a < 0, entonces I (f) = ( -∞, yv ]
Los términos de la función reciben los siguientes nombres:
f (x) = ax2 + bx +c
término cuadrático
término lineal
término independiente
La representación gráfica de una función cuadrática es una parábola.
1) Funciones de la forma : y = ax2
a > 0, las ramas de la parábola se dirigen hacia arriba
Ramas de la parábola
a < 0, las ramas se dirigen hacia abajo
0 < IaI < 1; la parábola se abre respecto del eje y
Amplitud de la parábola
IaI >1; la parábola se cierra respecto a dicho eje.
2) Funciones de la forma: y = ax2+ c
c > o; la gráfica se desplaza hacia arriba.
Corrimiento con el eje vertical
c < o; la gráfica se desplaza hacia abajo.
3) Funciones de la forma y = ax2 + bx
Corrimiento sobre el eje horizontal si a y b tienen el mismo signo, la gráfica de la
parábola se desplaza hacia la izquierda. Si a y b tienen distinto signo, la gráfica se
desplaza hacia la derecha.
Gráfica de la parábola
Para realizar el gráfico de una parábola, f(x) = ax2+ bx +c, se deben calcular los
elementos de la misma y luego representarla.
 Raíces de la parábola: Son los puntos de intersección de la gráfica y el eje
x, ello ocurre cuando f(x) = 0
Para hallar esos valores se emplea la fórmula resolvente de Bhaskara:
−𝑏 ± √𝑏2 − 4𝑎𝑐
𝑥=
2𝑎
 Vértices de la parábola: Es el punto donde la función alcanza su máximo o
mínimo valor. Las coordenadas del vértice son: V = (xv, yv)
Xv =
𝒙𝟏+𝒙𝟐
𝟐
ó
xv =
−𝒃
𝟐𝒂
yv = f (xv)
Este método solo se podrá emplear cuando la función tenga dos raíces reales
distintas; en caso de que ello no sea así haremos completación de
cuadrados.
 Eje de simetría: es la recta que tiene por ecuación x = xv. Divide a la parábola
en dos ramas simétricas.
 Ordenada al origen: Es el punto de intersección de la gráfica con el eje y,
es decir, f (0) = c
Posiciones relativas respecto del eje de abscisas
Las raíces de la función cuadrática, f (x) = ax2 + bx + c, se calculan mediante la
−𝑏±√𝑏2 −4𝑎𝑐
fórmula 𝑥 =
2𝑎
Al radicando b2- 4ac se lo llama discriminante, ya que el valor del mismo sirve para
discriminar la naturaleza de las raíces de la función y se lo simboliza con la letra
griega Δ (delta)
Δ = b2 – 4ac
1) Cuando Δ > 0, la gráfica tiene dos puntos de intersección con el eje x. la
función tiene dos raíces reales distintas.
Por ejemplo: f(x) = x2+ 2x -3  Δ = 16
2) Cuando Δ = 0, la gráfica tiene un punto de intersección con el eje x. La función
tiene dos raíces iguales o raíz doble (vértice de la parábola).
Por ejemplo: f(x) = x2 + 2x +1  Δ = 0
3) Cuando Δ < 0, la gráfica no tiene puntos de intersección con el eje x. Es decir,
no tiene raíces reales.
Por ejemplo: f(x) = x2+ 2x + 2  Δ = -4
Ecuación polinómica, canónica y factorizada.
La ecuación cuadrática puede ser expresada de distintas maneras:
Se desarrolla el cuadrado del binomio
Se aplica propiedad distributiva
CANÓNICA
POLINÓMICA
FACTORIZADA
f (x) = a (x – xv)2+ yv
f (x) = ax2 + bx + c
f (x) = a (x – x1) (x – x2)
Se busca el vértice o se completa cuadrados
Se buscan las raíces
Máximos y mínimos. Crecimiento y decrecimiento.
Decimos que una función es creciente en un intervalo de su dominio, cuando al
aumentar los valores de la variable independiente (x), aumentan los valores de la
variable dependiente (y = f (x)).
f (x) es creciente si: x1 > x2, entonces f (x1) > f (x2)
Decimos que una función es decreciente en un intervalo de su dominio, cuando al
aumentar los valores de la variable independiente, disminuyen los valores de la
variable dependiente.
f (x) es decreciente si: x1 > x2, entonces f (x1) < f (x2)
En general, dada la función f (x) = ax2+ bx + c, se verifica que:
Alcanza un mínimo en el vértice de la parábola.
1) Si a > 0, la función :
Decrece en el intervalo ( -
∞, xv)
Crece en el intervalo (xv, ∞)
Alcanza un máximo en el vértice de la parábola.
2) Si a < 0, la función:
∞, xv)
Decrece en el intervalo (xv, ∞)
Crece en el intervalo (-