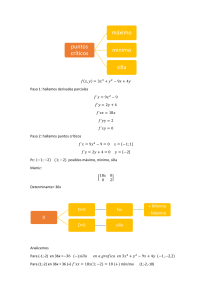
1 Micelanea . E: 3x2y C e y dx C x C xe 3y2 dy D 0. D: H Análisis
Anuncio

1 6 Micelanea . E: 3x 2 y C e y dx C x 3 C xe y 3y 2 dy D 0. D: H Análisis. Dada la forma diferencial de la ecuación y descartando los métodos: Separación de Variables, Homogéneas y Lineales, probamos el método de ED Exactas. Aquí M D 3x 2 y C e y & N D x 3 C xe y 3y 2 , luego: My D 3x 2 C e y D Nx ) la ED es exacta. Buscamos ahora un función f tal que: @f D M D 3x 2 y C e y I @x @f D N D x 3 C xe y @y (1) 3y 2 : (2) Si integramos (1) con respecto a x, hallamos: Z x f D .3x 2 y C e y / dx D x 3 y C xe y C k.y/: Si derivamos f con respecto a y, e igualamos a N usando (2) hallamos: @f D x 3 C xe y C k 0 .y/ D x 3 C xe y @y 3y 2 ) k 0 .y/ D 3y 2 ) k.y/ D y 3 : Así, la solución general de la ED está dada por x 3 y C xe y y 3 D C: 6. canek.azc.uam.mx: 23/ 11/ 2010