Respuesta a sinusoidal Métodos Diagramas de Bode Diagramas

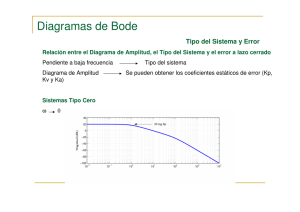
Respuesta a sinusoidal
Se alimenta una y se estudia a la salida del
estado estacionario.
x(t) = X sin(ωt), donde ω es la frecuencia.
Se varia la frecuencia del sinusoidal para ver
qué efectos tiene esto.
Se prueban las frecuencias “relevantes”.
Se junta la información sobre cómo se comporta
el sistema.
Diagramas de Bode
Una gráfica del logaritmo de la magnitd de la
función de transferencia sinusoidal.
Una gráfica del ángulo de fase.
O sea, el ángulo del vector G(jω).
Ambas contra la frecuencia, en escala logarítmica.
Se puede determinar hasta experimentalmente sin
contar con la función de transferencia.
En Octave: bode(sys) o bode([1, 2, 3], [4, 5, 6]).
Métodos
Analíticamente/matemáticamente:
Con series de Fourier para entradas periódicas.
Gráficamente:
Con diagramas tales como los de Bode y
Nyquist.
Ya casi no se ocupa hacerlos manualmente.
Usamos Octave.
Diagramas polares
Magnitud de G(jω) c.r.a. su ángulo fase en
coordenadas polares.
Como los que se dan en las especificaciones
técnicas de micrófonos y bocinas.
http://www.engr.usask.ca/classes/ME/431/notes/Note_14.pdf
Diagramas de Nyquist
Obviamente nyquist(sys) en Octave.
Criterio de estabilidad de Nyquist:
Una prueba a base de la respuesta en
frecuencia de un sistema de lazo abierto.
http://www.brains-minds-media.org/archive/1988/
http://www.facstaff.bucknell.edu/mastascu/econtrolhtml/Freq/Freq6.html
Propiedades a estudiar
Estabilidad
Ancho de banda
Relación ganancia-fase
Error en estado estacionario
Margen de ganancia y margen de fase