Control 1 Evaluaci´ on Continua 17-03-2009 Sistemas Autom´

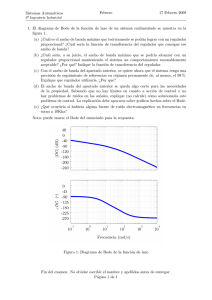
Sistemas Automáticos
Control 1 Evaluación Continua
17-03-2009
4º Ingenierı́a Industrial
1. Dibuje un diagrama de bloques genérico del lazo de realimentación incluyendo todos los elementos y variables que en él intervienen. Explique brevemente la función de cada elemento.
2. [Franklin 4.30(a)] El modelo en ecuaciones diferenciales de un motor de corriente continua,
con inductancia de inducido despreciable(La = 0) y par de perturbación w, se muestra a
continuación como
Ra
JRa
θ̈m + Ke θ̇m = va +
w
Kt
Kt
donde θm se mide en radianes. Dividiendo por el coeficiente de θ̈m , obtenemos
θ̈m + a1 θ̇m = b0 va + c0 w,
donde
a1 =
Kt
1
Kt Ke
, b0 =
, c0 = .
JRa
JRa
J
Con potenciómetros giratorios es posible medir el error entre θm y el ángulo de referencia
θref , o e = θref −θm . Con un tacómetro podemos mediar la velocidad del motor θ̇m . Considere
realizar una realimentación utilizando el error e y la velocidad del motor θ̇m de la siguiente
manera
va = K(e − TD θ̇m )
donde K y TD son ganancias a determinar.
(a) Dibuje un diagrama de bloques del sistema realimentado resultante, mostrando explı́citamente las variables θm y θ̇m .
(b) Obtener la función de sensibilidad de entrada.
3. Se pretende controlar un sistema de función de transferencia G(s) =
proponen dos alternativas:
1
s+a .
Para ello se
1. Un control en cadena abierta con un controlador Dol = Kol .
2. Un control en cadena cerrada con un controlador Dcl = Kcl . Para un análisis previo
se puede considerar un sensor ideal y que las ganancias del selector de referencia y del
sensor se compensan perfectamente.
Estudiar la sensibilidad de ambos sistemas ante la variación del parámetro a. ¿Cuál se verı́a
más afectado por la variación de este parámetro? ¿Cuál serı́a la sensibilidad de ambos a
una frecuencia de 1000/2π Hz ante variaciones de a ?
1
4. Un sistema cuya función de transferencia es G(s) = s(s+1)(s+10)
se pretende controlar en
cadena cerrada con un regulador proporcional de función de transferencia D(s) = 10. La
realimentación, suponiendo que el sensor utilizado es ideal y compensando su ganancia adecuadamente con el selector de referencia, se puede considerar unitaria. Utilizando MATLAB
se realizan las siguientes operaciones:
bode(D*G)
nyquist(D*G)
Obteniéndose las gráficas de las figuras 1 y 2.
Analice la estabilidad del sistema de todas las formas que conozca.
El examen continúa en el reverso de la página.
Página 1 de 2
17-03-2009 (cont.)
Sistemas Automáticos
4º Ingenierı́a Industrial
Bode Diagram
Magnitude (dB)
50
0
−50
−100
−150
Phase (deg)
−90
−135
−180
−225
−270
−2
10
−1
0
10
1
10
2
10
3
10
10
Frequency (rad/sec)
Figura 1: Resultado de bode(D*G)
Nyquist Diagram
Nyquist Diagram
1
0.1
0.8
0.08
0.6
0.06
0.04
Imaginary Axis
Imaginary Axis
0.4
0.2
0
−0.2
0.02
0
−0.02
−0.4
−0.04
−0.6
−0.06
−0.8
−0.08
−1
−0.1
−1.5
−1
−0.5
0
0.5
−0.3
(a) Nyquist
−0.25
−0.2
−0.15
−0.1
−0.05
Real Axis
Real Axis
(b) Aproximación al corte con el eje real
Figura 2: Resultado de nyquist(D*G)
Fin del examen. No olvidar escribir el nombre y apellidos antes de entregar.
Página 2 de 2
0