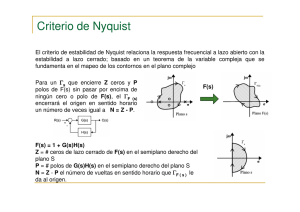
CRITERIO DE ESTABILIDAD DE NYQUIST Jonier Porras Duque Ingenierı́a Electrónica Universidad Distrital Franciso José de Caldas 1. Definición Considerar el siguiente sistema retroalimentado Figura 1: Sistema de control retroalimentado La función de transferencia del sistema es: C(s) = (R(s) − H(s))G(s) C(s) G(s) − H(s)G(s) = R(s) R(s) C(s) (1 + H(s)G(s)) = G(s) R(s) G(s) C(s) = R(s) 1 + H(s)G(s) La ecuación caracterı́stica del sistema es: 1 F (s) = 1 + H(s)G(s) Para analizar la estabilidad del sistema encontramos los ceros de F (s) que son los mismos polos de la función de transferencia. Para que el sistema sea estable todos los ceros de la función F (s) deben estar localizados en el semiplano izquierdo del plano s. La función de transferencia en lazo abierto (G(s)H(s)) nos permite obtener más fácil dichos ceros, por ello se suele trabajar con esta para aplicar el criterio de estabilidad de Nyquist. El criterio de estabilidad de Nyquist relaciona la respuesta en frecuencia en lazo abierto G(s)H(s) con el numero de raı́ces de la ecuación caracterı́stica 1+G(s)H(s) que se encuentran en el semiplano derecho del plano s. Como se analiza la ecuación de lazo abierto G(s)H(s), ya no analizamos el origen (punto 0+j0), sino que el punto ahora es otro. H(s)G(s) = F (s) − 1 = 1 − 0j Hacemos: P (s) = H(s)G(s) Los ceros de 1 + P (s) son los polos de la función de transferencia de lazo cerrado. son las raı́ces de la ecuación caracterı́stica. Los polos de 1 + P (s) son los polos de la función de lazo abierto. Diagrama de Nyquist Figura 2: Contorno y diagrama de Nyquist Un sistema retroalimentado es estable si el contorno Γp en el plano P(s) no rodea el punto (-1 + j0) cuando el número de polos de P(s) en la parte derecha del plano s es cero. 2 Un sistema de control retroalimentado es estable si en el contorno Γp el número de rodeos al punto (-1 + j 0) en el sentido contrario al movimiento de las manecillas del reloj es igual al número de polos de P(s) con partes reales positivas. El criterio de estabilidad de Nyquist por lo tanto se define en términos del punto (1+j0) en la gráfica polar. La proximidad a ese punto determina la estabilidad relativa de un sistema. Este criterio de estabilidad es muy útil para sistemas con retardos puros que no se pueden tratar con el criterio de Routh-Hurwitz y que son difı́ciles de analizar con el método del lugar de las raı́ces. Cómo aplicar el criterio de Nyquist 1) 2) 3) 4) Se define la trayectoria de Nyquist. Se construye la traza de P(s)(G(s)H(s)) en el plano P(s) Se obtiene el número de encierros del punto (-1 , j0) hechos por la traza de P(s). El criterio de Nyquist se obtiene de la ecuación (Criterio de Cauchy) N =Z −P donde: N : número de encierros del punto (−1, j0) hechos por la traza de P(s) Z : número de ceros de 1 + P (s) que están en el semiplano derecho (SPD) P : número de polos de 1 + P (s) que están en el SPD. (Polos de P(s)) Para que el sistema sea estable en lazo cerrado, Z debe ser igual a cero. Para que el sistema sea estable en lazo abierto, P debe ser igual a cero. En conclusión Para que un sistema de lazo cerrado sea estable, la traza de P(s) debe encerrar al punto (-1, j0) un número de veces igual al número de polos de P(s) que están en el semiplano derecho del plano s y los encierros, si los hay, deben ser hechos en la dirección del reloj. Si el punto (-1, j0) está encerrado por la traza de Nyquist, el sistema es inestable. 2. Ejemplo Función de transferencia: G(s)H(s) = k s(s + 4)(s + 5) 3 Figura 3: Trayectoria de Nyquist Tramo Tramo Tramo Tramo 1(T1): Se evalúa la función en 0+ < w < ∞ 2 (T2): Se evalúa la función en −∞ < w < ∞ 3 (T3): −∞ < w < 0− 4 (T4): 0− < w < 0+ Tramo 1: Primero reemplazamos a s=jw en G(s)H(s) k jw(jw + 4)(jw + 5) G(jw)H(jw) = G(jw)H(jw) = G(jw)H(jw) = (−w2 k + 4jw)(jw + 5) k −jw − 5w − 4w2 + 20jw 3 G(jw)H(jw) = 2 k −9w + jw(20−w2 ) 2 Separamos la parte real e imaginaria: k[−9w2 − jw(20−w2 )] G(jw)H(jw) = [−9w2 + jw(20−w2 )][−9w2 − jw(20−w2 )] G(jw)H(jw) = k[−9w2 − jw(20−w2 )] 81w4 + w2 (20−w2 )2 4 G(jw)H(jw) = − k9 81w2 + (20−w2 )2 −j k(20−w2 ) 81w3 + w(20−w2 )2 Ahora Reemplazamos los lı́mites de w: lı́mw→ − 0+ G(jw)H(jw) = − 9k − j∞ 400 lı́mw→ − ∞ G(jw)H(jw) = −0 − j0 Como pudo haber cambio de cuadrante, analizamos si hay puntos de cortes con el eje real: 0 = −j k(20−w2 ) 81w3 + w(20−w2 )2 √ w = 20 Este valor de w, lo reemplazamos en la ecuación de la parte real para encontrar el punto de corte: − k9 2 81(20) + (20 − 20) =− k 180 Figura 4: Plano F(s) del tramo 1 Tramo 2: Es la semircunferencia de radio infinito y donde −90 < θ < 90 s = Rejθ 5 G(Rejθ )H(Rejθ ) = jθ jθ lı́mR→ − ∞ G(Re )H(Re ) k Rejθ (Rejθ + 4)(Rejθ + 5) = k = 0e−j3θ Rejθ (Rejθ )(Rejθ ) Ahora evaluamos la función en diferentes valores de θ para ver su comportamiento θ = 90o G(Rej90 )H(Rej90 ) = 0e−j270 => θ=0 G(Re0 )H(Re0 ) = 0e0 => θ = −90 G(Re−j90 )H(Re−j90 ) = 0ej270 => Figura 5: Plano F(s) Tramo 2 Tramos 3: Reemplazamos a s=jw y variamos a w0− < w < ∞. Este mismo análisis se hizo en el tramo 1, solo que w tenı́a otros intervalos. G(jw)H(jw) = k(20−w2 ) − j 81w2 + (20−w2 )2 81w3 + w(20−w2 )2 − k9 lı́mw→ − −∞ G(jw)H(jw) = lı́mw→ − 0− G(jw)H(jw) = −0 − j0 − k9 + j∞ 400 La gráfica en el plano F(s) del tramo 3 es el la gráfica del tramo 1 reflejada sobre el eje real Tramo 4: Es la semircunferencia de radio que tiende a 0 y ángulo variando de −90 < θ < 90 s = εejθ G(εejθ )H(εejθ ) = εejθ (εejθ 6 k + 4)(εejθ + 5) Figura 6: Plano F(s) Tramo 3 jθ jθ lı́mε→ − 0 G(εe )H(εe ) = k εejθ (4)(5) = ∞e−jθ Ahora evaluamos la función en diferentes valores de θ para ver su comportamiento θ = 90o θ=0 θ = −90 => G(Rej90 )H(Rej90 ) = ∞e−90 G(Re0 )H(Re0 ) = ∞e0 => => G(Re−j90 )H(Re−j90 ) = ∞ej90 Figura 7: Plano F(s) Tramo 4 Por último unimos los tramos y construimos la gráfica de Nyquist y con ello se concluye si el sistema es estable o no 7 El sistema es estable, pues para que cumpla el criterio de estabilidad de Nyquist se necesita que no haya rodeos al punto −1 + 0j. Podemos ver que además no hay polos en el semiplano derecho de P(s), lo que concuerda con el criterio de estabilidad de Nyquist para lazo abierto (P = 0). Además el rango de k para que el sistema sea estable es: 0 ≤ k ≤ 180 Si k es mayor a 180 incluirı́a entonces el punto (−1, 0j), lo que implicarı́a que el sistema se vuelve inestable. 8