Ejemplo de Energía plano inclinado fricción

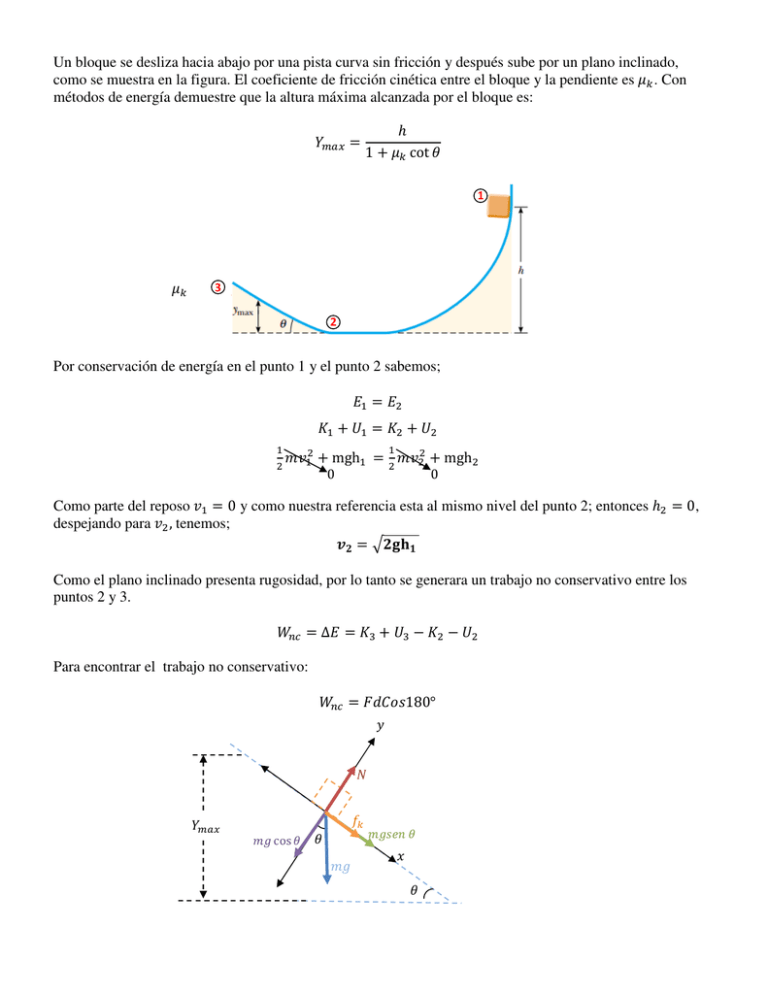
Un bloque se desliza hacia abajo por una pista curva sin fricción y después sube por un plano inclinado,
como se muestra en la figura. El coeficiente de fricción cinética entre el bloque y la pendiente es . Con
métodos de energía demuestre que la altura máxima alcanzada por el bloque es:
=
ℎ
1 + cot 1
3
3
2
Por conservación de energía en el punto 1 y el punto 2 sabemos;
= + = + + mgh = + mgh
0
0
Como parte del reposo = 0 y como nuestra referencia esta al mismo nivel del punto 2; entonces ℎ = 0,
despejando para ,tenemos;
= !
Como el plano inclinado presenta rugosidad, por lo tanto se generara un trabajo no conservativo entre los
puntos 2 y 3.
"#$ = ∆ = & + & − − Para encontrar el trabajo no conservativo:
"#$ = ()*+,180°
6
4
/ cos 3
/
/,01
5
7 (8 = 0
4 − / cos = 0
4 = / cos Como 3 = − 4 = − / cos , entonces:
"#$ = − )/ cos Para saber que es d, analizamos el triángulo rectángulo que se forma:
)
,01 =
)
) =
,01
Sustituyendo el valor de d en la ecuación de trabajo "#$ :
"#$ =
− / cos ,01
Igualando el trabajo no conservativo con el cambio de la energía mecánica:
9:; <=>? @ ABC D
EF#D
= & + & − − 0
− / cos 1
= mgh& − ,01
2
Sustituyendo :
ABC D
− / EF#D = g − I2gh J
0
Donde h& = 1
− /K+L = g − M2gh N
2
− cot = − h
Sacamos factor común ∶
+ cot = h
M1 + cot N = h
PQRS =
M! + TU VWX YN
Como h = h