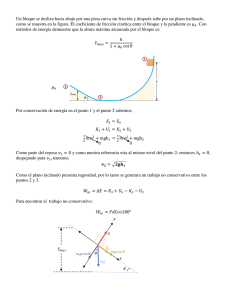
mgh mv 2 1 mgh mv 2 1 mgh mgh mv 2 1 mv 2 1 E E W + = +

Un vehículo de 1000 kg de masa está subiendo una cuesta con una inclinación del 10 %. La velocidad es de 72 km/h. Cuando faltan 100 m para llegar a la cumbre se le acaba la gasolina. a) Determinar si llega a la cumbre y, si es así, calcula su velocidad. Considera despreciable los rozamientos. b) Si el coeficiente de rozamiento con el suelo es de 0,2, ¿llegará a la cumbre? calcula la velocidad con la que llega. Sol: a) Vo=72 km/h=20 m/s Como no hay rozamiento y sin fuerza del motor, la ecuación sería: 1
1
1
1
Wtotal = ΔE c = − ΔEp → mv 2f − mv 2o = −(mgh f − mgho ) → mv 2f + mgh f = mv 2o + mgho
2
2
2
2
Aplicándolo a nuestro caso: Consideramos ho =0 , cuando se le acaba la gasolina, entonces calcularíamos la altura a la que sube, y con ello lo que se ha desplazado para ver si ha sido mayor o inferior a 100m: 1
1
1 2
mv o + mgho = mv 2f + mgho → ho = 0; y , v f = 0; m20 2 = m∙9,8∙h 2
2
2
h=20,4 m Como la pendiente es del 10%. 10 20,4
=
; X=204m 100
x
Según este resultado si llegaría a la cumbre. Como la cumbre está a 100 m de recorrido, su velocidad en la cumbre la tendríamos que calcular de la siguiente manera: 1
1
m20 2 = mv 2f + mgh 2
2
Teniendo en cuenta que cuando haya recorrido los 100 m, la altura que ha subido con respecto a cuando se le acabó la gasolina, se calcula de la siguiente manera: 10
x
= entonces x=1 m de altura 100 10
1 2 1
mv f = m20 2 − m∙9,8∙1 2
2
v=19,5 m/s b) Con rozamiento: Wtotal = ΔEc = − ΔEp + Wroza En este caso podemos hacerlo calculando el espacio que debe recorrer hasta que el coche se pare, es decir que su vf=0 Wroz = μN∙Δx∙cos 180 o , como estamos en un plano inclinado del 10% de pendiente senα = 0.1 → α = arcsen0,1 = 5,74 o , entonces: Wroz = μN∙Δx∙cos 180 o = μPy ∙Δx∙cos 180 o = μmg cos 5,74 o ∙Δx∙cos 180 1 2 1 2
mv f − mv o = −(mgh f − mgho ) + μmg cos α∙Δx∙cos 180 2
2
1
0 − m20 2 = −(mgΔh) + μmg cos α∙Δx∙cos 180 ; 2
La altura la tenemos que poner en función del espacio recorrido: 10 Δh
=
→ Δh = 0,1Δx 100 Δx
1
0 − m20 2 = −(mg0,1Δx) + 0,2m9,8 cos 5,74∙Δx∙(−1) 2
200 = Δx(0,98 + 0,2∙9,8∙cos 5,74 o ) → Δx =
Luego no llegaría a la cumbre 200
= 68,25m 0,98 + 0,2∙9,8 cos 5,74 o