º º h<

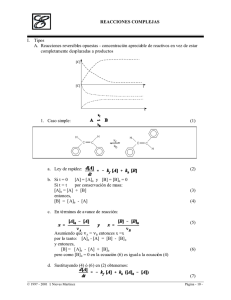
TEORIA DEL COMPLEJO ACTIVADO O ESTADO DE TRANSICIÓN
I.
Equilibrio:
A.
B.
A
+
B
º
…
X
º
P
Energía de vibración clásica = Energía de vibración cuántica:
=
h<
=
Ecuant
=
kBT
Eclas
(1)
(2)
Rapidez en que el complejo activado se mueve a través de la barrera de energía
potencial
(3)
(4)
C.
Por el equilibrio:
(5)
D.
Sustituyendo (5) en (4):
(6)
E.
Si definimos:
(7)
F.
Sustituyendo (7) en(6)
(8)
G.
II.
…
K se calcula por termodinámica estadística ypropiedades físicas fundamentales para
react ivos y complejo activado (largo de enlace, frecuencia de vibración, masas y
momento de iniercia).
…
Relación de K con parámetros termodinámicos:
A.
) G° = - RT ln K y
) G° = ) H° - T) S°
(9)
B.
(10)
C.
Sustituyendo (10) en (7):
(11)
III.
Asociación de Eyring con Arrhenius
(12)
A.
De la ecuación (7)
© 1997 - 2001 I. Nieves Martínez
Página - 19 -
T E O R I A C O M P L EJ O A C A T IV A D O
(13)
(14)
Pero:
Sustituyendo (14) en (13):
(15)
Pero:
(16)
Sustituyendo (16) en (15)
(17)
B.
Equivalencia con Arrhenius:
(18)
C.
Energía de activación equivale a:
(19)
Por lo tanto:
(20)
D.
Pero la ecuación (11)
Igualando (20) con (11):
(21)
(22)
© 1997 - 2001 I. Nieves Martínez
Página - 20 -
TEORÍA DE COLISIONES
I.
Reacción bimolecular en el estado gaseoso.
A.
Redistribución de energía para choques intermoleculares (movimiento relativo)
1.
Esferas rígidas:
(1)
2.
Distribución:
(2)
3.
Energía:
(3)
(4)
B.
Rapidez:
(5)
C.
Constante específica de rapidez de acuerdo a la teoría de colisiones:
(6)
(7)
(8)
(9)
(10)
(11)
© 1997 - 2001 I. Nieves Martínez
Página - 21 -