REACCIONES COMPLEJAS I. Tipos A. Reacciones reversibles

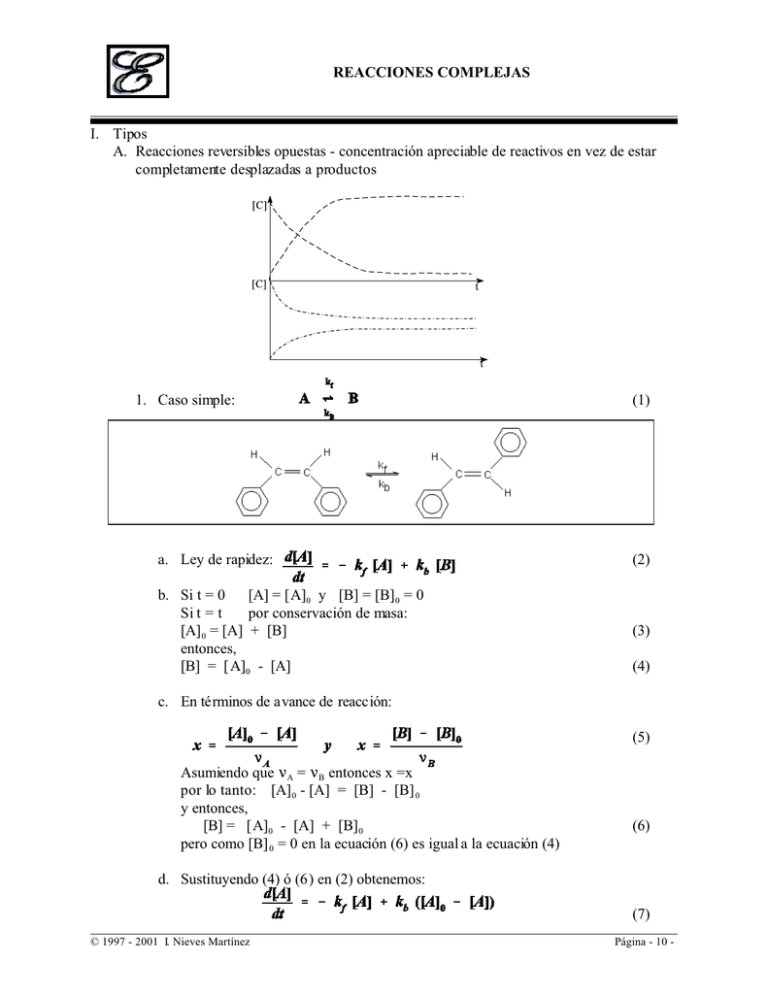
REACCIONES COMPLEJAS
I. Tipos
A. Reacciones reversibles opuestas - concentración apreciable de reactivos en vez de estar
completamente desplazadas a productos
1. Caso simple:
(1)
a. Ley de rapidez:
(2)
b. Si t = 0
[A] = [A]0 y [B] = [B] 0 = 0
Si t = t
por conservación de masa:
[A] 0 = [A] + [B]
entonces,
[B] = [A]0 - [A]
(3)
(4)
c. En términos de avance de reacción:
(5)
Asumiendo que <A = <B entonces x =x
por lo tanto: [A] 0 - [A] = [B] - [B] 0
y entonces,
[B] = [A]0 - [A] + [B] 0
pero como [B] 0 = 0 en la ecuación (6) es igual a la ecuación (4)
(6)
d. Sustituyendo (4) ó (6) en (2) obtenemos:
(7)
© 1997 - 2001 I. Nieves Martínez
Página - 10 -
REACCIONE S COMPL EJAS
(8)
e. Simplificando: Cuando t º 4 Rf = Rb
y por lo tanto
y [A] = [A] eq
entonces la ecuación (8) se puede expresar:
(9)
y por lo tanto:
(10)
Sustituyendo (10) en (8):
(11)
(12)
f. Separando variables e integrando:
(13)
(14)
(15)
(16)
B. Reacciones paralelas de primer orden:
© 1997 - 2001 I. Nieves Martínez
Página - 11 -
REACCIONE S COMPL EJAS
1. Ley de rapidez:
(17)
2. Separando variables e integrando:
(18)
(19)
(20)
3. Para el producto B la ley de rapidez:
(21)
Sustituyendo (20) en (21):
(22)
Separando variables e integrando:
(23)
(24)
Para determinar la constante si t = 0 [B]0 = 0 y entonces la ecuación (24) se puede
expresar:
(25)
(26)
por lo tanto:
(27)
© 1997 - 2001 I. Nieves Martínez
Página - 12 -
REACCIONE S COMPL EJAS
Susytituyendo (27) en (24):
(28)
4. Determinación de [C] por conservación de masa:
[A] 0 = [A] + [B] + [C] en cualquier t
por lo tant o: [C] = [A] 0 - [A] - [B]
(29)
(29)
(30)
5. Observen que:
Si las reacciones no son reversibles y k 1 >>>k2 las concentraciones siguen un control
cinético
Si las reacciones son reversibles y
las especies siguen un control termodinámico.
C. Reacciones consecutivas:
(CH3)2CO º C=CO + CH4
C=CO
º 1/2 C2H4 + CO
(31)
1. a t =0
[A] = [A]0
y [B] = [B]0 = 0 = [C]0 = [C]
2. Ley de rapidez:
(32)
(33)
(34)
Como [B] = [B] 0 = 0 = [C]0 = [C] entonces separando variables e integrando la
ecuación (32)
(35)
© 1997 - 2001 I. Nieves Martínez
Página - 13 -
REACCIONE S COMPL EJAS
(36)
Sustituyendo (36) en (33):
(37)
Rearreglando:
(38)
El lado izquirdo de la ecuación (38) es una ecuación diferencial del tipo:
(39)
La ecuación (38) se resuelve si se multiplica por ek2t a ambos lados
(40)
(41)
Separando variables:
(42)
Integrando:
(43)
(44)
Para determinar la constante c: t = 0 [B] 0 = 0
(45)
Sustituyendo (45) en (44):
(46)
Dividiendo (46) entre ek2t a ambos lados:
(47)
© 1997 - 2001 I. Nieves Martínez
Página - 14 -
REACCIONE S COMPL EJAS
Sustituyendo (47) en (34)
(48)
Sería mucho más fácil si usaramos conservación de masa donde: [C] = [A] 0 - [A] [B], combinando y sacando denominador común
(49)
3. Gráficas
a. para k1 >>>> k2 paso lento es el # 2
t4
[C] º [A] 0
[C] = f (k2)
[C]t
. [A]0 (1 - e-k2t)
b. para k2 >>> k1 paso lento es el # 1
1. [B] es extremadamente reactiva:
[C]t . [A] 0 (1 - e-k1t) . [A]rx
(50)
(51)
pero k2 >> k1 entonces,
º
(52)
La ecuación (52) es una fracción pequeña y [B] es constante
c. Concentración estacionaria:
Esto es cierto en un intervalo de tiempo
t>0yt<4
4. Aproximación del estado estacionario
a. Condiciones para utilizarla
© 1997 - 2001 I. Nieves Martínez
Página - 15 -
REACCIONE S COMPL EJAS
1. Especie bien reactiva: kdesap >>> kforma
i.e. átomos, radicales, iones, especies excitadas:
[Productos] >> [I] << [Reac]
2.
3. Se utiliza para sistemas complejos; (reacción en cadana)
(53)
(54)
(55)
depende del paso lento.
5. Reacciones en cadana:
H2 + Br2 º 2HBr
a. Ley de rapidez:
(56)
1. El producto está actuando como inhibidor en etapas lejos de t º 0.
2. En t º 0 n º 3/2
b. Mecanismo: Christiansen, Herzefeld y Polanyi
k1
1. M + Br2 º 2 Br• + M iniciacón
(57)
k2
2. Br + H2 º HBr + H•
•
propagación
(58)
k3
3. H• + Br2 º HBr + Br• propagación
(59)
k4
4. HBr + H º Br• + H2
•
inhibición
(60)
k5
5. M + 2 Br º Br2 + M terminación
•
(61)
c. Rapidez de reacción neta = rapidez de formación + rapidez de desaparición
(62)
© 1997 - 2001 I. Nieves Martínez
Página - 16 -
REACCIONE S COMPL EJAS
Como los intermediarios no se pueden determinar experiment almente se asume la
aproximación del estado estacionario para esas especies.
(63)
(64)
Sumando (63) y (64):
Despajando:
(65)
De la ecuación (63):
(66)
(67)
Sustituyendo (65) en (67):
(68)
Sustituyendo (68) y (65) en (62)
(69)
Sacando denominador común y luego factor común combinando y luego dividiendo entre
k4[Br4] toda la expresión arriba y abajo:
(70)
© 1997 - 2001 I. Nieves Martínez
Página - 17 -
REACCIONE S COMPL EJAS
Dividiendo arriba y abajo por k3/k4
(71)
Si:
(72)
Entonces las ecuación (71) es igual a la experimental.
II. Aproximación del paso lento ó determinante
A. I- + OClº
Cl+ OIB. Ley de rapidez experimental:
(73)
(74)
(75)
(76)
(77)
k3 >> k2
por lo tanto:
(78)
© 1997 - 2001 I. Nieves Martínez
Página - 18 -