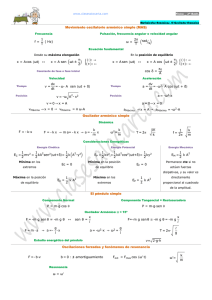
Solución de la ecuación de Schrödinger Oscilador armónico

SOLUCIÓN DE LA ECUACIÓN DE
SCHRÖDINGER
OSCILADOR ARMÓNICO
Equipo 2
OSCILADOR ARMÓNICO CLÁSICO

Sistema que contenga un componente sobre el
que actúa una fuerza restauradora proporcional a
su desplazamiento desde el equilibrio.
OSCILADOR ARMÓNICO
Mecánica clásica
Mecánica Cuántica
La energía puede tener cualquier
nivel continuo
La energía solo puede tener
valores discretos
Cambios en los niveles de
energía pueden tomar cualquier
valor
Cambios en los niveles de
energía solo ocurren en cuantos
El cuerpo puede estar en reposo
en x=0
El nivel de energía mínimo es
No existe reposo absoluto en x=0
OSCILADOR ARMÓNICO CUÁNTICO


Se puede obtener la ecuación de Schrodinger de
un oscilador armónico utilizando el potencial
clásico.
La ecuación de Schrodinger con esta forma de
potencial es:
APROXIMACIÓN DE LA SOLUCIÓN


Se sugiere la siguiente forma:
Téngase en cuenta que esta forma (una función
gaussiana), satisface el requisito de ir a cero en el
infinito, por lo que es posible normalizar la
función de onda.
RESOLVIENDO LA ECUACIÓN DE
SCHRODINGER

Sustituyendo esta función en la ecuación de
Schrodinger, mediante la evaluación de la
segunda derivada de la función de onda.
SOLUCIÓN
POLINOMIO DE HERMITE

Cuando la ecuación de Schrodinger para el
oscilador armónico se resuelve mediante el
método de series, las soluciones contienen este
conjunto de polinomios, llamado polinomios de
Hermite.
POLINOMIO DE HERMITE
ψ
FUNCIONES DE ONDA
ESQUEMA TRIDIMENSIONAL DE NIVELES
DE ENERGÍA Y PROBABILIDAD
ESQUEMA TRIDIMENSIONAL DE NIVELES
DE ENERGÍA Y PROBABILIDAD
PROBLEMA

Curva que corresponde a la probabilidad
|Ψ1² = ψ*ψ para el estado n = 10 del oscilador
armónico simple. ¿Cómo ilustra este diagrama el
principio de correspondencia de Bohr?
CONCLUSIONES



La probabilidad de encontrar
cualquier valor dado de x es ψ2
el
oscilador
en
Conforme aumenta n la función de onda presenta
mas crestas en el pozo de potencial, lo cual
corresponde a una longitud de onda mas corta y por
lo tanto tiene mayor energía.
A medida que aumenta el número cuántico, la
distribución de probabilidad se parece más a la del
oscilador clásico (principio de correspondencia), y
para niveles bajos (moléculas), el modelo cuántico
describe mejor esta distribución de probabilidad.
BIBLIOGRAFIA

LEVINE, Ira N. Quantum chemistry, Boston,
Allyn and bacon, 1974. Pp 48-67.