γ γ χ

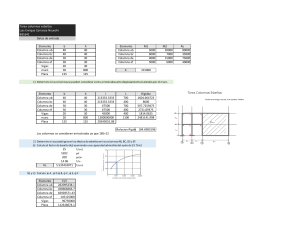
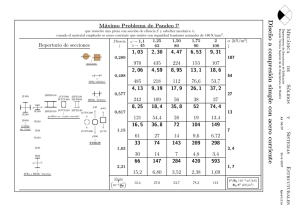
VIGAS PILAR
PROBLEMA Nº8
Verificar si la pieza del problema anterior (pieza biarticulada de sección HEA160, fabricada
con un acero S235, de 4m de longitud) es capaz de soportar un momento flector uniforme
en este caso respecto de su eje fuerte de magnitud My.Sd=15kNm que actúa junto con el
esfuerzo axil de compresión Nsd =250kN.
SOLUCIÓN:
Las características mecánicas y geométricas de la sección HEA160 son:
My.Sd
En esta ocasión deberemos de hacer una comprobación de pandeo global en el plano de
flexión y adicionalmente asegurarnos de que la pieza no se agota por pandeo lateral. En
esta situación, las expresiones de comprobación que se deben verificar son:
k y ⋅ M y.Sd
N Sd
+
≤1
χ y ⋅ A ⋅ ( f y / γ M 1 ) W pl . y ⋅ ( f y / γ M 1 )
-1-
VIGAS PILAR
k LT ⋅ M y.Sd
N Sd
+
≤1
χ z ⋅ A ⋅ ( f y / γ M 1 ) χ LT ⋅ Wpl . y ⋅ ( f y / γ M 1 )
En la primera expresión precisamos calcular la esbeltez normalizada λy a partir de la cual
obtendremos el coeficiente de reducción χy para el pandeo global de la pieza respecto del
eje fuerte y-y.
λ 
0, 5
λ y =  y  ⋅ [β A ]
 λ1 
siendo:
λ1 = π [ E / f ]0,5 = 93,9ε = 93,9 ;
y
λy =
β A = 1 (sección Clase 1)
lcr 400cm
=
= 60,88
i y 6,57cm
λ 
 60,88  0,5
0,5
λ y =  y  ⋅ [β A ] = 
 ⋅ 1 = 0,631
 93,9 
 λ1 
En esta situación con flexión respecto del eje fuerte de la sección y relaciones geométricas
h 152
=
= 0,95 < 1,2 ; t f ≤ 40mm
b 160
corresponde utilizar la curva de pandeo b. De ella obtenemos para la esbeltez λy=0,631
χy= 0,8204
También precisamos calcular el coeficiente ky que utilizaremos para mayorar el momento
flector aplicado My.Sd y depende de µy, que a su vez se obtiene a partir del coeficiente de
momento equivalente β M.ψ. Este último esta relacionado con la distribución de momentos.
ky = 1−
µ y ⋅ N Sd
;
χ y ⋅ A⋅ fy
µ y = λ y ⋅ (2 ⋅ β M .Ψ − 4) +
k y ≤ 1,5
W pl . y
− 1 ; µ y ≤ 0,9
Wel . y
-2-
VIGAS PILAR
Dado que el momento flector de cálculo My.Sd es uniforme en toda la pieza (ψ=1) el
coeficiente de momento equivalente β M.ψ valdrá:
β M .Ψ = 1,8 − 0,7 ⋅ Ψ = 1,1
Así los coeficientes µy y ky serán:
Ahora ya estamos en condiciones de verificar el cumplimiento de la expresión de interacción
k y ⋅ M y.Sd
N Sd
+
≤1
χ y ⋅ A ⋅ ( f y / γ M 1 ) W pl . y ⋅ ( f y / γ M 1 )
podemos decir que efectivamente la sección soporta el pandeo global en el plano fuerte.
Comprobación de la pieza a pandeo lateral fuera del plano de flexión.
Se trata de verificar el cumplimiento de la expresión ya indicada anteriormente
k LT ⋅ M y.Sd
N Sd
+
≤1
χ z ⋅ A ⋅ ( f y / γ M 1 ) χ LT ⋅ Wpl . y ⋅ ( f y / γ M 1 )
-3-
VIGAS PILAR
Como novedades tendremos que obtener el coeficiente reductor de pandeo lateral χLT en
función de la esbeltez normalizada λLT
λ 
1/ 2
λLT =  LT  ⋅ (β w )
 λ1 
Wel . y

(Clase 3)
β w = W
pl . y

;
siendo β w = 1 (Clases 1 y 2); 
 β = Weff . y (Clase 4)
 w W pl . y

λ1 = π [ E / f ]0,5 = 93,9ε = 93,9
y
teniendo en cuenta que ψ=1 (momento uniforme) y que k=1 (extremos articulados), el
coeficiente C1=1, de modo que la esbeltez λLT, la esbeltez normalizada λLT y el coeficiente
de reducción de pandeo lateral χLT tomando la curva a (sección laminada) serán:
-4-
VIGAS PILAR
La otra novedad de la comprobación de la pieza a pandeo lateral consiste en determinar el
coeficiente mayorador kLT del momento aplicado My.Sd . Dependiente de µLT, que a su vez se
obtiene a partir de la esbeltez normalizada (λz = 1,0703) y del coeficiente de momento
equivalente (β M.LT =1,1) relacionado con la distribución de momentos flectores.
k LT = 1 −
µ LT ⋅ N Sd
;
χz ⋅ A⋅ fy
µ LT = 0,15 ⋅ λz ⋅ β M . LT − 0,15 ;
k LT ≤ 1,0
µ LT ≤ 0,9
conocidas todas las variables estamos en condiciones de llevar a cabo la comprobación
k LT ⋅ M y.Sd
N Sd
+
≤1
χ z ⋅ A ⋅ ( f y / γ M 1 ) χ LT ⋅ Wpl . y ⋅ ( f y / γ M 1 )
0,548 + 0,312 = 0,86 < 1
Esto nos confirma que la sección propuesta sería válida
-5-