Diagramas Polares El diagrama polar de una función de
Anuncio
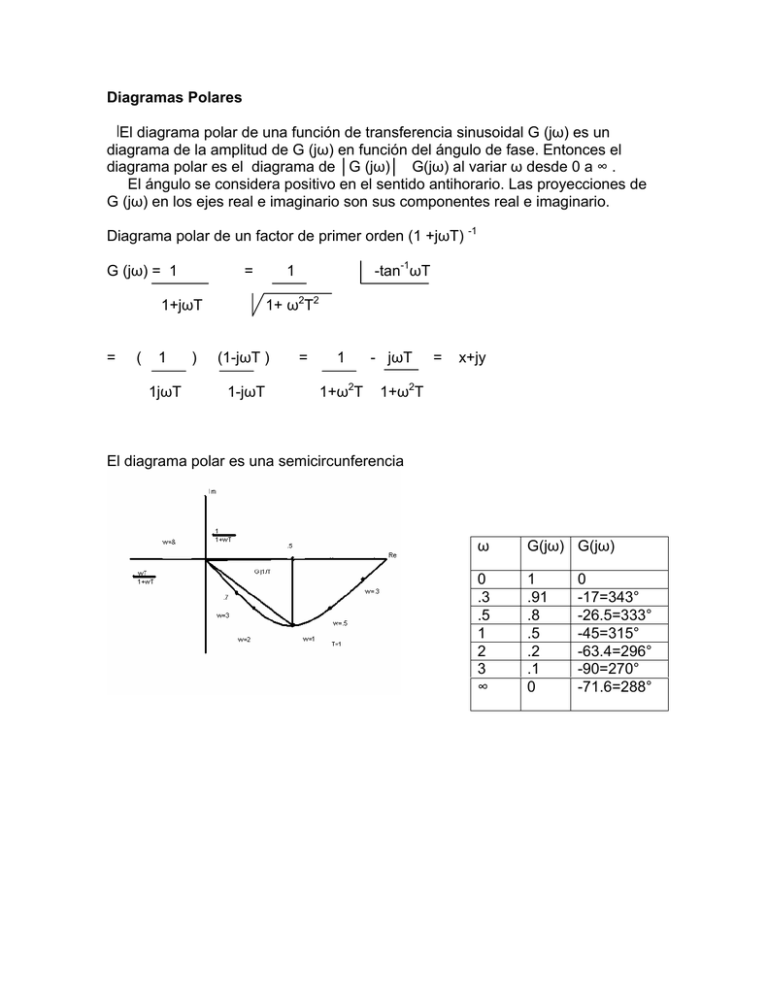
Diagramas Polares El diagrama polar de una función de transferencia sinusoidal G (jω) es un diagrama de la amplitud de G (jω) en función del ángulo de fase. Entonces el diagrama polar es el diagrama de │G (jω)│ G(jω) al variar ω desde 0 a ∞ . El ángulo se considera positivo en el sentido antihorario. Las proyecciones de G (jω) en los ejes real e imaginario son sus componentes real e imaginario. Diagrama polar de un factor de primer orden (1 +jωT) -1 G (jω) = 1 = 1+ ω2T2 1+jωT = ( 1 1jωT ) -tan-1ωT 1 (1-jωT ) 1-jωT = 1 1+ω2T - jωT = x+jy 1+ω2T El diagrama polar es una semicircunferencia ω G(jω) G(jω) 0 .3 .5 1 2 3 ∞ 1 .91 .8 .5 .2 .1 0 0 -17=343° -26.5=333° -45=315° -63.4=296° -90=270° -71.6=288° En forma rectangular quedaría : ω 0 .3 .5 1 2 3 & X 1 .91 .8 .5 .2 .1 0 Y 0 -.27 -.4 -.5 -.4 -.3 0 El diagrama polar también puede obtenerse directamente del diagrama de Bode Ejemplo: G(s) = 1/(s+1) se puede representar como : G(jω) = 1 1+jωT Amplitud en db= -20log | 1+ jωT | db = -20 log 1+ω2T2 si T=1 db = -20 log Ǿ= 1 1 +ωT Ǿ= -tan-1ω Tabulando en forma de Bode: ω G(jω) G(jω) .1 .2 .5 1 2 0db 1 0db 1 -1db=.89 3db=.707 -7db=.45 -6° -12° -30° -45° -64° 1+ω2T2 5 10 0 1.5 -14db=.2 -20db=.1 1db=1 .5db=.56 -78° -84° 0° -56° Si estos mismos valores lo aplicamos a una gráfica polar (cambiando los valores de amplitud de db a valores lineales nos queda : El lugar de P (jω) es el mismo en coordenadas polares ó rectangulares. La forma como se escoge es de forma analítica ó como datos experimentales. Para observar la complejidad de las gráficas polares se muestra la gráfica de 2 G(s)= G (jω)= s2 + s + 2 -tan-1 ω 1 (1-ω2/2)2 + ω2/4 2 – ω2 Ω G(jω) .2 .4 .8 1 2 4 10 0 1.5 1.2 1.3 1.4 1.05 1.06 1.26 1.41 .70 .137 .020 1 1.3 1.5 1.51 1.42 -tan-1 ω 2-w2 -5.82° -12.26° -30.46° -45° -135° -164° -174° 0° -99°-65° -76° -88° Retardo de transporte. El retardo de transporte es debido a los retrasos inherentes en las respuestas de los sistemas físicos, y en Laplace se representan como una exponencial de la forma G (jω) = e –jωT La fase se representa como: cos ωT-j senωT Ej. Obtener el diagrama polar de G (jω) = e-jωL G (jω)= 1+ jωT 1 e-jωL - 1+ jωT ) 1+ω2T2 G (jω) = 1 Ǿ (jw) = (-ωL-tan-1 ωT) en radianes 1+ω2T2 Si L=1 y T=1 la tabulación queda ω 0 .5 1 2 3 10 .2 .6 .8 1.5 2.5 G(jω) 1 .9 .7 .44 .31 .09 .98 .85 .78 .55 .37 G(jω) 0° -55.26=305° -103=257° -178=181° 116° 297° 337° 294° 275° 217° |48° ω 3 4 5 G(jω) .3 .24 .196 G(jω) -243° -305° -365°