Apertura monopulso ∫∫ ∫ ∫

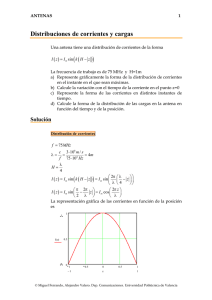
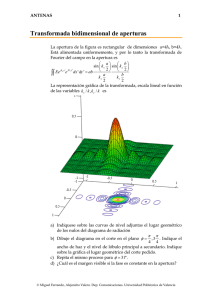
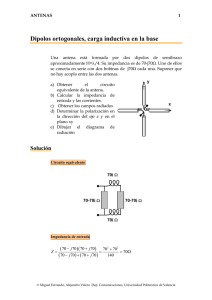
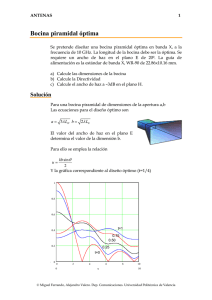
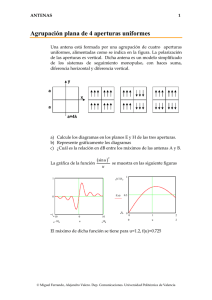
ANTENAS
1
Apertura monopulso
Una antena que se utiliza habitualmente en antenas reflectoras de
seguimiento (sistemas monopulso) es una bocina piramidal
multimodo.
La bocina se puede simular como una apertura, iluminada con los
modos TE10 y TE20.
La expresión de los
campos
para
dichos
modos es
y
G
⎛π x ⎞
E10 = E10 cos ⎜
⎟ yˆ
⎝ a ⎠
G
⎛ 2π x ⎞
E20 = E20 sin ⎜
⎟ yˆ
⎝ a ⎠
E
b
x
a
a = 10λ b = 10λ
a) Se pide calcular el diagrama de radiación para una apertura con
iluminación coseno en el eje x, y uniforme en el y,
correspondiente al modo TE10.
b) Estudie la forma del diagrama diferencia, correspondiente al
modo TE20.
Solución
Los campos radiados por una apertura con polarización vertical son
Eθ = j
⎛η
⎞
e − jkr
jk y '
sin φ ⎜ cos θ + 1⎟ ∫∫ E ( x ', y ' ) e jkx x 'e y dx ' dy '
2λ r
⎝ Z0
⎠ s'
⎛η
⎞
e − jkr
jk y '
cos φ ⎜ + cos θ ⎟ ∫∫ E ( x ', y ') e jkx x 'e y dx ' dy '
Eφ = j
2λ r
⎝ Z0
⎠ s'
La apertura con distribución coseno
∫∫ E ( x ', y ') e
s'
jk x x '
e
jk y y '
dx ' dy ' = E0 ∫ f ( x ' ) e jkx x ' dx ' ∫ g ( y ')e
x'
jk y y '
dy '
y'
Las transformadas correspondientes son
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
2
⎛k a⎞
cos ⎜ x ⎟
π
⎝ 2 ⎠
F (k x , a ) = ∫ f ( x ') e jkx x ' dx ' = a
2
2 ⎛ π ⎞ ⎛ k x a ⎞2
a
−
⎜ ⎟ −⎜
⎟
2
⎝2⎠ ⎝ 2 ⎠
⎛k b⎞
b
sin ⎜ y ⎟
2
jk y '
⎝ 2 ⎠
G (k y , b) = ∫ g ( y ') e y dy ' = b
⎛ k yb ⎞
b
−
⎜
⎟
2
⎝ 2 ⎠
a
2
Apertura con distribución diferencia
En este caso las expresiones son idénticas, exceptuando el diagrama
en el plano horizontal.
La
transformada de Fourier se puede realizar integrando
directamente, o bien como un array de dos aperturas de dimensiones
a/2, separadas la misma distancia
y
b
E
a/2
F (k x , a) =
a
2
∫
−
F (k x , a) =
a
2
a
2
∫
−
a
2
E
x
a/2
⎛k a⎞
cos ⎜ x ⎟
kx a
kx a
π
⎝ 4 ⎠ ⎛ e j 4 − e− j 4 ⎞
f ( x ' ) e jkx x ' dx ' = a
⎜
⎟
4 ⎛ π ⎞2 ⎛ k x a ⎞2 ⎝
⎠
⎜ ⎟ −⎜
⎟
2
4
⎝ ⎠ ⎝
⎠
⎛k a⎞
cos ⎜ x ⎟
π
⎝ 4 ⎠ 2 j sin ⎛ k x a ⎞
f ( x ') e jkx x ' dx ' = a
⎜
⎟
2
4 ⎛ π ⎞ ⎛ kx a ⎞2
⎝ 4 ⎠
⎜ ⎟ −⎜
⎟
⎝2⎠ ⎝ 4 ⎠
La representación gráfica de los diagramas se puede hacer a partir
del producto de los diagramas de la apertura por el de array
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
3
Diagrama plano E
Corresponde a una distribución uniforme de dimensión 10λ
1
1
0.8
0.6
f ( θ , 0.01deg)
0.4
0.2
−8
1.523 ×10
0
1.5
1
0.5
0
−π
0.5
1
1.5
θ
π
2
2
Diagrama suma plano H
Corresponde a una distribución coseno de dimensión 10λ
1
1
0.8
0.6
f 2( θ )
0.4
0.2
−6
7.069 ×10
0
1.5
−π
2
1
0.5
0
θ
0.5
1
1.5
π
2
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
4
Diagrama de una apertura de dimensión 5λ
Distribución coseno de dimensión 5λ
1
1
0.8
0.6
f 2( θ )
0.4
0.2
−5
7.833 ×10
0
1.5
1
0.5
0
−π
0.5
1
1.5
θ
π
2
2
Efecto de interferencia y producto de diagramas
Producto por una agrupación uniforme de 2 elementos espaciados 5λ
1
1
0.8
0.6
f 2( θ ) ⋅ i( θ )
i( θ )
0.4
0.2
0
0
1.5
−π
1
0.5
0
0.5
1
1.5
θ
2
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
π
2