Dada la función f(x) =

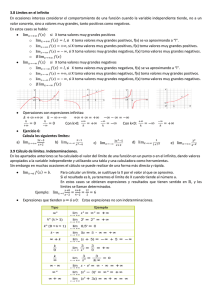
Dada la función f(x) =
x²  2
2x  1
1) Calcula sus asíntotas.
2) Calcula los máximos y mínimos.
3) Represéntala gráficamente.
SOLUCIÓN :
1) f(x) =
x²  2
. Df = R - -1/2. Además en x = -1/2 el numerador no se anula por lo que
2x  1
se tiene lim f (x)   con lo que x = -1/2 es una asíntota vertical.
x1/ 2
f(x) es una fracción algebraica en la que el numerador es de grado una unidad mayor
que el del denominador, si hacemos la división en el cociente tendremos un polinomio de grado
uno, que será la asíntota oblicua:
El sumando
x²  2
1
1 9/4
= x 
.
2x  1 2
4 2x  1
x²  2
9/4
1
1
 0, cuando x   , por lo que
 x  , cuando x  ,
2x  1
2x  1
2
4
siendo por tanto y =
1
1
x  , la asíntota oblicua.
2
4
Otra forma de calcular la asíntota oblicua consiste en calcular los límites:
m = lim
x
f (x)
y n = lim  f (x)  mx , con lo que se tendría la recta y = mx + n:
x
x
2
x = 1,
m = lim
x 2x  1
2
x
1
1 
 x²  2 1 

n = lim f (x)  x = lim 
 x =  ,
x
x
4
2 
 2x  1 2 

por lo que y =
1
1
x  es la asíntota oblicua.
2
4
2) Se trata de ver cuándo f(x) toma valores máximos y mínimos. Para calcular estos
valores derivamos e igualamos a 0 para localizar los puntos de tangente horizontal.
Conociendo el crecimiento (f’(x) > 0), y decrecimiento (f’(x) < 0) a ambos lados de
los puntos, sabremos si se trata de un máximo (f (x) pasa de creciente a decreciente)
o de un mínimo (f (x) pasa de decreciente a creciente).
f'(x) =
2(x  2)(x  1)
2(x²  x  2)
=
, f'(x) = 0 para x1 = 1, x2 = -2.
(2x  1)²
(2x  1)²
El signo de f’(x) depende del numerador, que representa una parábola cóncava que
corta al eje OX en x1 = 1 y x2 = -2. Por tanto:
para x  (- ,  2)  (1,  ) , f'(x) > 0 y
 1
para x  (-2, 1) -   , f'(x) < 0.
 2
Así, f crece de -
 a -2, decrece de -2 a  1 y de  1 a 1 y crece de 1 a +  .
2
2
Por tanto, (-2, -2) es un máximo y (1, 1) es mínimo.
3) Con estos datos, la representación gráfica quedaría: