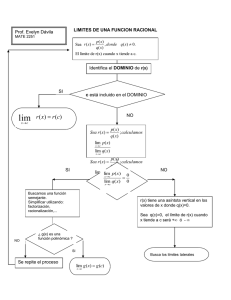
El Cálculo. Louis Leithold. Séptima edición en español. ISBN 970

El Cálculo. Louis Leithold. Séptima edición en español. ISBN 970-613-182-5
Ejercicios de repaso para el capítulo 3. Ejercicio 121, página 295.
Si p y q son números racionales tales que p + q = 1, demuestra que la recta y = x + (ap + bq) es una asíntota oblícua
p
q
de la grá…ca de f (x) = (x + a) (x + b) .
Solución:
Primero recordemos la de…nición de asíntota oblicua:
La grá…ca de la función f
siguientes es verdadera:
tiene a la recta
y = mx + b
como una asíntota oblicua si alguna de las porposiciones
(i) lim [f (x)
(mx + b)] = 0, y para algún número real M > 0, f (x) 6= mx + b siempre que x > M ;
(ii) lim [f (x)
(mx + b)] = 0, y para algún número real M < 0, f (x) 6= mx + b siempre que x < M ;
x!+1
x! 1
Recordemos también el teorema generalizado del binomio:
Si y
entonces
son números reales con
r
( + ) =
1
X
r
k
k=0
> j j (esta condición garantiza la convergencia) y r es cualquier número complejo,
r k k
Tenemos entonces
p
(x + a) =
1
X
k=0
p
k
xp
q
l
xq l bl
k k
a
y
q
(x + b) =
1
X
l=0
y por lo tanto podemos escribir el producto,
p
q
(x + a) (x + b) =
1
X
k;l=0
p
k
q
l
xp+q
p
k
q
l
x1
k l k l
a b
como p + q = 1,
p
q
(x + a) (x + b) =
1
X
k;l=0
k l k l
a b
Escribiendo explicitamente los primeros términos, tenemos
p
q
(x + a) (x + b) = x + pa + qb +
+
p
2
q
1
x
2 2
a b+
q
2
p
2
x
1 2
p
1
x
2
a +
ab2 +
q
2
x
p
2
1 2
b +
q
2
x
p
1
q
1
x
1
ab+
3 2 2
a b + ::: =
y por tanto
p
q
(x + a) (x + b)
x
(ap + bq) = x + pa + qb +
p
2
x
1
1 2
a +
q
2
x
1 2
b +
p
1
q
1
x
1
ab+
+
p
2
=
p
2
+
p
2
=
1
X
k;l=0
k+l>1
q
1
x
2 2
a +
q
2
x
2 2
1 2
x
q
1
p
k
q
2
a b+
x
q
l
x1
b +
p
1
q
2
p
1
1 2
a b+
p
1
x
2
q
1
x
2
p
2
ab2 +
x
ab2 +
1
q
2
x
3 2 2
q
2
x
3 2 2
a b + :::
x
(ap + bq) =
ab+
p
2
a b + ::: =
k l k l
a b
a1 a2 a3
+ + + :::. Además,
Notese que todos los términos son potencias negativas de x; es decir, la serie es de la forma
x x2 x3
como p y q son números racionales tales que p + q = 1, la serie no termina nunca y todos los términos tienden a cero
cuando x ! 1; así que
lim [f (x)
x! 1
(mx + b)] = 0
Falta demostrar que para algún número real M > 0, f (x) 6= mx + b siempre que x > M y que para algún número real
M < 0, f (x) 6= mx + b siempre que x < M . Es claro que esto es cierto, ya que la curva se acerca tanto como uno quiera
a la recta x (ap + bq), sin embargo, es claro que siempre que x sea …nito no pueden ser iguales.
Con esto terminamos la demostración.
2