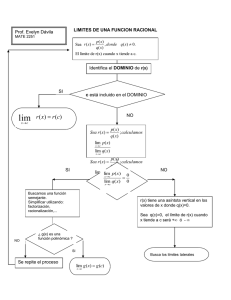
Asíntotas

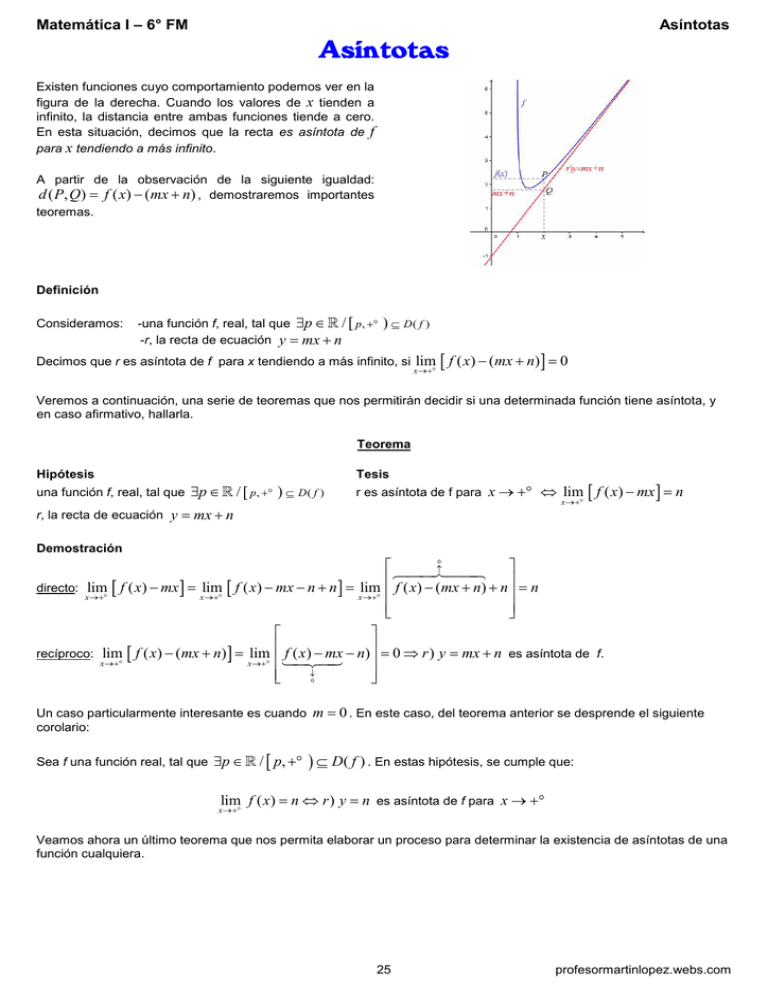
Matemática I – 6° FM
Asíntotas
Asíntotas
Existen funciones cuyo comportamiento podemos ver en la
figura de la derecha. Cuando los valores de x tienden a
infinito, la distancia entre ambas funciones tiende a cero.
En esta situación, decimos que la recta es asíntota de f
para x tendiendo a más infinito.
A partir de la observación de la siguiente igualdad:
d ( P, Q ) = f ( x) − (mx + n) , demostraremos importantes
teoremas.
Definición
Consideramos:
-una función f, real, tal que ∃p ∈ ℝ / [ p , +∞ ) ⊆ D ( f )
-r, la recta de ecuación y = mx + n
Decimos que r es asíntota de f para x tendiendo a más infinito, si
lim [ f ( x) − (mx + n) ] = 0
x →+∞
Veremos a continuación, una serie de teoremas que nos permitirán decidir si una determinada función tiene asíntota, y
en caso afirmativo, hallarla.
Teorema
Hipótesis
una función f, real, tal que
Tesis
∃p ∈ ℝ / [ p , +∞ ) ⊆ D ( f )
r es asíntota de f para
x → +∞ ⇔ lim [ f ( x) − mx ] = n
r, la recta de ecuación y = mx + n
x →+∞
Demostración


↑


directo: lim [ f ( x ) − mx ] = lim [ f ( x ) − mx − n + n ] = lim f ( x ) − ( mx + n) + n = n


x →+∞
x →+∞
x →+∞






recíproco: lim [ f ( x ) − ( mx + n) ] = lim f ( x ) − mx − n) = 0 ⇒ r ) y = mx + n es asíntota de f.

x →+∞
x →+∞ 
↓


0
0
Un caso particularmente interesante es cuando m = 0 . En este caso, del teorema anterior se desprende el siguiente
corolario:
Sea f una función real, tal que
∃p ∈ ℝ / [ p, +∞ ) ⊆ D( f ) . En estas hipótesis, se cumple que:
lim f ( x) = n ⇔ r ) y = n es asíntota de f para x → +∞
x →+∞
Veamos ahora un último teorema que nos permita elaborar un proceso para determinar la existencia de asíntotas de una
función cualquiera.
25
profesormartinlopez.webs.com
Matemática I – 6° FM
Asíntotas
Teorema
Consideramos:
•
•
∃p ∈ ℝ / [ p, +∞ ) ⊆ D( f )
r, la recta de ecuación y = mx + n
f, una función real tal que
En estas condiciones, demostraremos que : Si r asíntota de f para
x → +∞ , entonces lim
x →+∞
f ( x)
=m
x
Demostración
0


↑


f ( x)
f ( x) − mx
 f ( x)


lim
= lim 
− m + m  = lim
+ m = m
x →+∞
x →+∞
x →+∞ 

x
x
x




↓

+∞

Ahora, pues, con la ayuda de estos simplísimos teoremas, elaboraremos un procedimiento que nos permitirá determinar
si una función particular tiene o no una recta asíntota para x → +∞ , y en caso afirmativo, poder hallarla.
Procedimiento para el estudio de asíntota de f con
x → +∞
Si lim f ( x) = n, entonces r ) y = n es asíntota de f para x → +∞
 x →+∞

1) Calculamos lim f ( x ) Si lim f ( x ) = ±∞, vamos al paso 2
x →+∞
x →+∞

Si ∃ lim f ( x), entonces f no tiene asíntota para x → +∞
x →+∞


Si

f ( x) Si
2) Calculamos lim

x →+∞
x 
Si


Si
f ( x)
= m ≠ 0, entonces vamos al paso 3
x →+∞
x
f ( x)
lim
= 0, f no tiene asíntota para x → +∞ (decimos que hay D.A.//Ox)
x →+∞
x
lim f ( x) = ±∞, f no tiene asíntota para x → +∞ (decimos que hay D.A.//Oy )
lim
x →+∞
∃ lim f ( x), f
x →+∞
no tiene asíntota para x
→ +∞
Si lim [ f ( x) − mx ] = n, entonces r ) y = mx + n es asíntota de f
 x →+∞

3) Calculamos lim [ f ( x ) − mx ] Si lim [ f ( x ) − mx ] = ±∞, f no tiene asíntota para x → +∞ (hay D.A.//y = mx )
x →+∞
x →+∞

Si ∃ lim [ f ( x) − mx ] , f no tiene asíntota para x → +∞
x →+∞

26
profesormartinlopez.webs.com
Matemática I – 6° FM
Asíntotas
Observaciones
1) Una definición, teoremas y procedimiento análogos existen para
x → −∞
2) Un comportamiento relacionado con el estudiado, es el referente a las
direcciones asintóticas.
f : f ( x) = Lx presenta una dirección
asintótica paralela al eje Ox para x → +∞ (D.A. // Ox ). Observemos el
comportamiento de la gráfica de esta función para x → +∞ :
Así, por ejemplo, decimos que la función
Y la función g : g ( x ) = e tiene dirección asintótica paralela al eje Oy para x → +∞ .
Pero, además de observar el comportamiento del gráfico de g para x → +∞ , observemos que hay asíntota para
x → −∞ , y que ésta es el eje Ox .
x
Ejercicios
1) Estudia las asíntotas de las siguientes funciones:
2 x2 + x + 1
x+3
a.
f : f ( x) =
b.
f : f ( x) = e x ( x + 1)
c.
f : f ( x) = L( x + 1)
d.
f : f ( x) = L( x + 1) + x
e.
f : f ( x) = L
x +1
+ 3x + 2
x
2) Justifica los resultados enunciados en el “procedimiento para el estudio de asíntota de
27
f para x → +∞ ”
profesormartinlopez.webs.com