ejerpolpol33
Anuncio

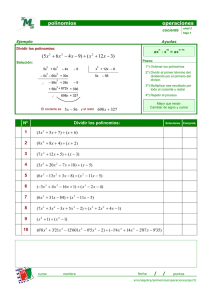
polinomios operaciones cociente Ejemplo nivel 3 hoja 3 Ayudas Dividir los polinomios: n ax : x = a x ( x − 6 x + 11x − 6) ÷ ( x − 4) 3 2 n–1 Pasos: Solución: 3 x 3 2 – 6x 2 –x + 4x ⁄ – 2x 2 2 + 11x –6 2 – 8x x 1º) Ordenar los polinomios 2º) Dividir el primer término del dividendo por el primero del divisor. – 2x + 3 + 11x 3º) Multiplicar ese resultado por todo el cociente y restar + 2x – 8x ⁄ + 3x –6 – 3x + 12 ⁄ 4º) Repetir el proceso hasta que el grado sea menor que el del cociente +6 El cociente es Nº x –4 x2 − 2x +3 Estas divisiones se hacen más fácil con la Regla de Ruffini y el resto 6 Dividir los polinomios: 1 (x4+5x3-2x3-6x+4) ÷ (x – 3 ) 2 (x4+2x3+7x2-16x+11) ÷ (x – 4) 3 (2x5+3x4-5x3-6x2-11x+12) ÷ (x –1) 4 (2x4-3x3+6x2-8x+4) ÷ (x –5) 5 (x4+4x3+6x2+7x+1) ÷ (x + 2) 6 (x8+x7+x6+x5+x4+x3+x2+x+1) ÷ (x –1) 7 (x4++3x2+6) ÷ (x –2) 8 (2x3-5x2+4x-7) ÷ (x –3) 9 (x6-3x5+4x4-7x3+12x2-9x-11) ÷ (x –1) 10 (x4+3x3-2x2-5x+9) ÷ (x +2) curso nombre Soluciones fecha / / Comprob. puntos xms/algebra/polinomios/operaciones/ejer33