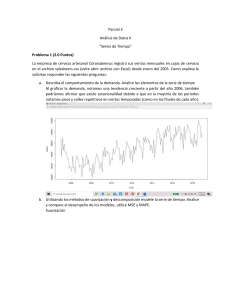
5.1 Modelo clásico de series de tiempo y sus componentes Una serie de tiempo es una secuencia de datos observados a intervalos de tiempo regulares. Los modelos clásicos de series de tiempo se utilizan para analizar y predecir valores futuros basados en observaciones pasadas. Estos modelos intentan capturar las estructuras y patrones inherentes en los datos. Los componentes principales de las series de tiempo son: 1. Tendencia (T): Representa la dirección general a largo plazo del comportamiento de la serie de tiempo. Puede ser ascendente, descendente o constante. La tendencia captura el cambio gradual a lo largo del tiempo. 2. Estacionalidad (S): Refleja patrones repetitivos y regulares en la serie de tiempo que ocurren en periodos específicos, como días, meses o trimestres. Por ejemplo, las ventas de helados pueden ser mayores en verano y menores en invierno. 3. Ciclos (C): Similar a la estacionalidad, pero los ciclos ocurren en intervalos irregulares y a menudo están asociados con fenómenos económicos o empresariales. Los ciclos pueden durar varios años y no son tan predecibles como la estacionalidad. 4. Aleatoriedad o Ruido (R): Componente impredecible que representa la variabilidad residual no explicada por los otros componentes. El ruido incluye todos los factores no sistemáticos o eventos aleatorios que afectan la serie de tiempo. 5.1.1. Análisis de fluctuaciones El análisis de fluctuaciones es una técnica utilizada en estadística y en series de tiempo para examinar las variaciones a corto plazo en los datos y entender la naturaleza de estas variaciones. Este análisis es fundamental para identificar patrones, tendencias y anomalías en datos temporales. A continuación, se detallan los aspectos clave del análisis de fluctuaciones. Componentes de las Fluctuaciones 1. Fluctuaciones Aleatorias (Ruido): Representan las variaciones impredecibles que no siguen un patrón específico. Se deben a factores aleatorios y eventos no sistemáticos. En el análisis de series de tiempo, estas fluctuaciones se tratan como ruido que puede dificultar la identificación de otros componentes significativos. 2. Fluctuaciones Estacionales: Ocurren a intervalos regulares y están relacionadas con períodos específicos del tiempo (por ejemplo, temporadas del año). Reflejan patrones repetitivos y predecibles. Ejemplo: Variaciones en las ventas de ciertos productos durante diferentes estaciones del año. 3. Fluctuaciones Cíclicas: Son similares a las estacionales, pero no tienen una periodicidad fija. Relacionadas con ciclos económicos, como expansiones y contracciones económicas. Ejemplo: Ciclos de negocio que afectan el desempeño económico en un horizonte de varios años. Métodos de Análisis 1. Descomposición de Series de Tiempo: Separar la serie en sus componentes (tendencia, estacionalidad, ciclos y ruido) para analizar cada uno por separado. Se puede realizar mediante métodos como la descomposición clásica aditiva o multiplicativa. 2. Análisis Espectral: Utiliza la transformada de Fourier para identificar frecuencias predominantes en las fluctuaciones de la serie de tiempo. Es útil para detectar ciclos y patrones repetitivos en los datos. 3. Autocorrelación: Mide la correlación entre valores en diferentes momentos en la serie de tiempo. Ayuda a identificar la presencia de patrones repetitivos y la duración de ciclos y estacionalidades. 4. Modelos ARIMA: Capturan diferentes aspectos de las fluctuaciones mediante componentes autorregresivos, de media móvil e integración. Son adecuados para modelar y predecir series de tiempo con fluctuaciones complejas. 5. Suavizamiento: Técnicas como el suavizamiento exponencial y el filtro de Kalman se utilizan para reducir el ruido y resaltar patrones significativos en los datos. El suavizamiento exponencial simple y el método de Holt-Winters son comunes para tratar fluctuaciones estacionales y de tendencia. 5.1.2. Análisis de tendencias El análisis de tendencias es una parte fundamental del análisis de series de tiempo que se centra en identificar y comprender la dirección general en la que se mueven los datos a lo largo del tiempo. Aquí tienes los conceptos clave relacionados con este análisis: Conceptos Clave 1. Tendencia: Definición: Es la dirección general o patrón que siguen los datos a lo largo del tiempo. Características: Puede ser ascendente (creciente), descendente (decreciente) o lateral (sin cambio significativo). Identificación: Se puede observar visualmente mediante gráficos de series de tiempo o mediante técnicas de modelado estadístico. 2. Descomposición de Series de Tiempo: Definición: Es el proceso de separar una serie de tiempo en sus componentes individuales, como tendencia, estacionalidad, variación cíclica y variación irregular. Métodos: Se utilizan técnicas como el método de promedios móviles, el método de suavización exponencial y el método de descomposición clásica. 3. Modelado de Tendencias: Definición: Es el proceso de ajustar un modelo matemático o estadístico a los datos para capturar la tendencia subyacente. Métodos: Incluyen modelos de regresión lineal, modelos de suavización exponencial, modelos auto regresivos integrados de medias móviles (ARIMA), entre otros. 4. Pronóstico de Tendencias: Definición: Es la predicción de la dirección futura de la tendencia en la serie de tiempo. Técnicas: Se utilizan técnicas de pronóstico, como la extrapolación de modelos ajustados o el uso de modelos de series de tiempo para prever la tendencia futura. 5. Medidas de Tendencia Central: Definición: Son medidas estadísticas utilizadas para resumir la tendencia central de un conjunto de datos. Ejemplos: Incluyen la media, la mediana y la moda. Uso: Proporcionan información sobre la ubicación típica de los datos y ayudan a identificar patrones de tendencia. 6. Validación de la Tendencia: Definición: Es el proceso de evaluar la validez de la tendencia identificada en los datos. Métodos: Incluyen análisis de residuos, pruebas estadísticas de significancia y comparación con datos externos o teoría relevante. 5.1.3. Análisis de variaciones cíclicas El análisis de variaciones cíclicas en series de tiempo se enfoca en identificar y comprender las fluctuaciones que ocurren en intervalos irregulares pero repetitivos, a menudo relacionadas con ciclos económicos, financieros o de negocios. Estas variaciones cíclicas son diferentes de las variaciones estacionales porque no tienen una periodicidad fija y pueden durar varios años. Conceptos Clave 1. Ciclo Económico: Expansión: Periodo de crecimiento económico, aumento de producción y empleo. Recesión: Periodo de contracción económica, disminución de producción y empleo. Pico: Punto más alto del ciclo económico antes de que comience la recesión. Valle: Punto más bajo del ciclo económico antes de que comience la expansión. 2. Duración y Amplitud: Duración: Tiempo que toma completar un ciclo completo (expansión y recesión). Amplitud: Diferencia entre los puntos máximos y mínimos del ciclo. 5.1.4. Medición de variación estacional o irregular. La medición de la variación estacional o irregular es un paso crucial en el análisis de series de tiempo, especialmente cuando se trabaja con datos que muestran patrones estacionales o ciclos irregulares. Aquí están los conceptos clave relacionados con este proceso: Conceptos Clave 1. Variación Estacional: Definición: Refleja los patrones repetitivos que ocurren en la serie de tiempo en el mismo período cada año (por ejemplo, estacionalidad en ventas navideñas). Características: Puede ser causada por factores como el clima, días festivos, estaciones del año, etc. Efectos: La variación estacional puede distorsionar la interpretación de las tendencias subyacentes si no se tiene en cuenta. 2. Variación Irregular: Definición: Representa las fluctuaciones impredecibles o aleatorias que no siguen un patrón específico y no se pueden atribuir a la estacionalidad, tendencia o ciclos conocidos. Características: Puede ser causada por eventos inesperados, como desastres naturales, cambios en la economía, crisis políticas, etc. Impacto: La variación irregular puede dificultar la identificación de patrones significativos en los datos. 3. Descomposición de Series de Tiempo: Definición: Es el proceso de separar una serie de tiempo en sus componentes individuales, incluyendo tendencia, estacionalidad, ciclo y variación irregular. Métodos: Se utilizan técnicas como el método de promedios móviles, el método de suavización exponencial y el método de descomposición clásica. 4. Método de Descomposición Clásica: Definición: Es un enfoque estadístico para descomponer una serie de tiempo en sus componentes de tendencia, estacionalidad y variación irregular. Proceso: Implica ajustar modelos separados para cada componente y luego combinarlos para obtener la serie de tiempo descompuesta. Aplicación: Permite analizar y comprender mejor los diferentes factores que contribuyen a la variación en los datos. 5. Ajuste Estacional: Definición: Es el proceso de eliminar la variación estacional de una serie de tiempo para revelar la tendencia subyacente y la variación irregular. Métodos: Se utilizan técnicas como el método de promedios móviles, el método de suavización exponencial y el ajuste estacional basado en la descomposición clásica. Objetivo: Facilita la identificación de patrones de comportamiento a largo plazo y la realización de pronósticos más precisos. 6. Anomalías Estacionales: Definición: Son desviaciones significativas de los patrones estacionales típicos en una serie de tiempo. Causas: Pueden ser el resultado de eventos inusuales, cambios en el comportamiento del consumidor, modificaciones en la oferta y la demanda, etc. Identificación: Requiere un análisis cuidadoso de los datos y puede implicar la corrección de datos anómalos para mejorar la precisión del modelo. 5.2 Aplicación de ajustes estacionales La aplicación de ajustes estacionales es un proceso esencial en el análisis de series de tiempo para eliminar la variación estacional y resaltar la tendencia subyacente y la variación irregular. Aquí tienes los conceptos clave relacionados con esta aplicación: Conceptos Clave 1. Ajuste Estacional: Definición: Es el proceso de eliminar la variación estacional de una serie de tiempo para revelar la tendencia subyacente y la variación irregular. Objetivo: Facilita la identificación de patrones de comportamiento a largo plazo y la realización de pronósticos más precisos al eliminar la influencia de la estacionalidad en los datos. Métodos: Se utilizan técnicas como el método de promedios móviles, el método de suavización exponencial y el ajuste estacional basado en la descomposición clásica. 2. Descomposición de Series de Tiempo: Definición: Es el proceso de separar una serie de tiempo en sus componentes individuales, incluyendo tendencia, estacionalidad, ciclo y variación irregular. Métodos: Se utilizan técnicas como el método de promedios móviles, el método de suavización exponencial y el método de descomposición clásica. 3. Componentes de la Serie de Tiempo: Tendencia: La dirección general en la que se mueven los datos a largo plazo. Estacionalidad: Los patrones que se repiten regularmente en la serie de tiempo. Variación Irregular: Las fluctuaciones impredecibles o aleatorias que no siguen un patrón específico. Ciclo: Las oscilaciones recurrentes que no siguen un patrón estacional fijo y pueden abarcar varios años. 4. Ajuste Estacional Basado en Descomposición Clásica: Definición: Implica descomponer la serie de tiempo en sus componentes de tendencia, estacionalidad y variación irregular, y luego ajustar o eliminar la estacionalidad. Proceso: Se ajusta la estacionalidad dividiendo la serie de tiempo por el componente estacional y multiplicando por un factor de ajuste. 5. Factor de Ajuste Estacional: Definición: Es el factor utilizado para ajustar o eliminar la estacionalidad en la serie de tiempo. Cálculo: Se obtiene dividiendo los datos originales por la componente estacional correspondiente en la descomposición de la serie de tiempo. 6. Evaluación del Ajuste Estacional: Validación: Es importante evaluar la efectividad del ajuste estacional para asegurar que se haya eliminado adecuadamente la variación estacional. Métricas: Se pueden utilizar métricas como el coeficiente de determinación (𝑅2R2) para evaluar la proporción de la variabilidad explicada por el ajuste estacional. 5.3 Pronósticos basados en factores de tendencia y estacionales Los pronósticos basados en factores de tendencia y estacionales implican prever valores futuros de una serie de tiempo teniendo en cuenta tanto la tendencia a largo plazo como los patrones estacionales recurrentes. Aquí tienes los conceptos clave relacionados con este proceso: Conceptos Clave 1. Tendencia: Definición: Es la dirección general en la que se mueven los datos a largo plazo, representando el cambio sistemático en el tiempo. Características: Puede ser ascendente, descendente o lateral. Identificación: Se puede identificar mediante métodos como el método de mínimos cuadrados, el método de promedios móviles, o la descomposición de series de tiempo. 2. Estacionalidad: Definición: Refleja los patrones repetitivos que ocurren en la serie de tiempo en el mismo período cada año. Efectos: Puede ser causada por factores como el clima, días festivos, estaciones del año, etc. Identificación: Se puede identificar mediante técnicas de descomposición de series de tiempo. 3. Pronóstico Basado en Tendencia: Definición: Es el pronóstico que considera solo la tendencia a largo plazo en los datos y no tiene en cuenta la variación estacional. Métodos: Se utilizan técnicas como el método de mínimos cuadrados, el método de suavización exponencial o el ajuste de modelos de regresión. 4. Pronóstico Basado en Factores Estacionales: Definición: Es el pronóstico que incorpora los efectos estacionales en la serie de tiempo, pero no considera la tendencia a largo plazo. Métodos: Se ajusta la estacionalidad de los datos utilizando técnicas como el método de descomposición clásica o el ajuste estacional basado en promedios móviles. 5. Pronóstico Basado en Tendencia y Estacionalidad: Definición: Es el pronóstico que tiene en cuenta tanto la tendencia a largo plazo como los patrones estacionales recurrentes en los datos. Métodos: Se combinan modelos de pronóstico de tendencia y estacionalidad para prever los valores futuros de la serie de tiempo. 6. Evaluación del Pronóstico: Métricas de Desempeño: Se utilizan métricas como el error cuadrático medio (ECM), el error absoluto medio (MAE) o el coeficiente de determinación (𝑅2R2) para evaluar la precisión del pronóstico. Validación Cruzada: Se divide la serie de tiempo en conjuntos de entrenamiento y prueba para evaluar la precisión del pronóstico en datos no vistos. 5.3.1. Método de mínimos cuadrados El método de mínimos cuadrados es una técnica estadística utilizada para encontrar la mejor línea de ajuste que minimiza la suma de los cuadrados de las diferencias (residuos) entre los valores observados y los valores predichos por el modelo. A continuación, se presentan los conceptos clave relacionados con el método de mínimos cuadrados: Conceptos Clave 1. Modelo Lineal: La forma más simple del modelo de mínimos cuadrados es una línea recta que se ajusta a un conjunto de datos. Ecuación del modelo lineal: 𝑌𝑡=𝑎+𝑏𝑡+𝜖𝑡Yt=a+bt+ϵt 𝑌𝑡Yt: Valor de la variable dependiente en el tiempo 𝑡t. 𝑎a: Intercepto (valor de 𝑌Y cuando 𝑡=0t=0). 𝑏b: Pendiente (cambio en 𝑌Y por unidad de cambio en 𝑡t). 𝜖𝑡ϵt: Término de error o residuo en el tiempo 𝑡t. 2. Residuos: Los residuos son las diferencias entre los valores observados (𝑌𝑡Yt) y los valores predichos (𝑌^𝑡Y^t) por el modelo. Fórmula del residuo: 𝑒𝑡=𝑌𝑡−𝑌^𝑡et=Yt−Y^t. 3. Suma de los Cuadrados de los Residuos (SSR): Es la suma de los cuadrados de todos los residuos. Fórmula: 𝑆𝑆𝑅=∑𝑡=1𝑛𝑒𝑡2=∑𝑡=1𝑛(𝑌𝑡−𝑌^𝑡)2SSR=∑t=1net2=∑t=1n (Yt−Y^t )2. El objetivo del método de mínimos cuadrados es minimizar esta suma. 4. Cálculo de los Parámetros 𝑎a y 𝑏b: Estos parámetros se calculan de manera que minimicen la SSR. Fórmulas para 𝑎a (intercepto) y 𝑏b (pendiente): 𝑏=𝑛∑𝑖=1𝑛𝑡𝑖𝑌𝑖−∑𝑖=1𝑛𝑡𝑖∑𝑖=1𝑛𝑌𝑖𝑛∑𝑖=1𝑛𝑡𝑖2−(∑𝑖=1𝑛𝑡𝑖)2b=n∑i=1nti2−(∑i=1n ti)2n∑i=1ntiYi−∑i=1nti∑i=1nYi 𝑎=𝑌ˉ−𝑏𝑡ˉa=Yˉ−btˉ 𝑌ˉYˉ: Media de los valores observados. 𝑡ˉtˉ: Media de los tiempos. 5. Coeficiente de Determinación (𝑅2R2): Mide la proporción de la variabilidad total en la variable dependiente que es explicada por el modelo. Fórmula: 𝑅2=1−𝑆𝑆𝑅𝑆𝑆𝑇R2=1−SSTSSR, donde 𝑆𝑆𝑇SST es la suma total de los cuadrados, 𝑆𝑆𝑇=∑𝑡=1𝑛(𝑌𝑡−𝑌ˉ)2SST=∑t=1n (Yt−Yˉ)2. 6. Ajuste del Modelo y Predicciones: Una vez calculados 𝑎a y 𝑏b, se puede usar el modelo para predecir nuevos valores de 𝑌Y para cualquier 𝑡t. Ecuación de predicción: 𝑌^𝑡=𝑎+𝑏𝑡Y^t=a+bt. 5.3.2. Método de promedios móviles El método de promedios móviles es una técnica utilizada en el análisis de series de tiempo para suavizar los datos y resaltar tendencias subyacentes al calcular promedios de valores sucesivos en ventanas de tiempo. Aquí tienes los conceptos clave relacionados con este método: Conceptos Clave 1. Promedio Móvil Simple (SMA): Definición: Calcula el promedio de un número fijo de valores adyacentes en la serie de tiempo. Fórmula: SMA𝑡=𝑌𝑡+𝑌𝑡−1+⋯+𝑌𝑡−𝑛+1𝑛SMAt=nYt+Yt−1+⋯+Yt−n+1 donde 𝑌𝑡Yt es el valor en el tiempo 𝑡t y 𝑛n es el tamaño de la ventana del promedio. Uso: Suaviza las fluctuaciones a corto plazo y resalta las tendencias a largo plazo en la serie de tiempo. 2. Promedio Móvil Ponderado (WMA): Definición: Calcula el promedio ponderado de un número fijo de valores adyacentes, asignando pesos diferentes a cada valor. Fórmula: WMA𝑡=∑𝑖=0𝑛−1𝑤𝑖𝑌𝑡−𝑖∑𝑖=0𝑛−1𝑤𝑖WMAt=∑i=0n−1wi∑i=0n−1wi Yt−i donde 𝑤𝑖wi es el peso asignado al 𝑖i-ésimo valor y 𝑛n es el tamaño de la ventana del promedio. Uso: Permite dar más peso a los valores más recientes, lo que hace que el promedio sea más sensible a los cambios recientes. 3. Ventana de Promedio: Definición: Es el número de puntos de datos utilizados para calcular el promedio móvil en cada paso. Impacto: Una ventana más larga suaviza más la serie de tiempo, mientras que una ventana más corta la hace más sensible a las fluctuaciones. 4. Factor de Suavización: Definición: Parámetro utilizado en algunos métodos de promedios móviles (como el método de suavización exponencial) para ajustar la sensibilidad del promedio a los cambios recientes. Valor: Generalmente se encuentra en el rango de 0<𝛼<10<α<1, donde valores más cercanos a 1 dan más peso a los valores recientes. 5. Desplazamiento de la Ventana: Definición: Es el proceso de mover la ventana de promedio un paso adelante en el tiempo después de calcular cada promedio. Efecto: Permite calcular múltiples promedios móviles a lo largo de la serie de tiempo y suavizar aún más los datos. 5.3.3. Método de suavización exponencial El método de suavización exponencial es una técnica utilizada en el análisis de series de tiempo para suavizar los datos y generar pronósticos, otorgando mayor peso a los datos más recientes. Aquí tienes los conceptos clave relacionados con este método: Conceptos Clave 1. Suavización Exponencial Simple (SES): Definición: Es un método de suavización exponencial que asigna un peso exponencialmente decreciente a los valores de la serie de tiempo. Fórmula de Pronóstico: 𝑌^𝑡+1=𝛼⋅𝑌𝑡+(1−𝛼) ⋅𝑌^𝑡Y^t+1=α⋅Yt+(1−α) ⋅Y^t donde 𝛼α es el factor de suavización (generalmente en el rango de 0<𝛼<10<α<1), 𝑌𝑡Yt es el valor observado en el tiempo 𝑡t, y 𝑌^𝑡Y^t es el pronóstico en el tiempo 𝑡t. 2. Suavización Exponencial Doble (DES): Definición: Extiende SES para series de tiempo que exhiben tanto tendencia como estacionalidad. Componentes: Incluye un término adicional para modelar la tendencia en la serie de tiempo. Fórmulas: Pronóstico de Nivel: 𝑌^𝑡+1=𝛼⋅𝑌𝑡+(1−𝛼) ⋅(𝑌^𝑡+𝑇𝑡) Y^t+1=α⋅Yt+(1−α) ⋅(Y^t+Tot) Pronóstico de Tendencia: 𝑇^𝑡+1=𝛽⋅(𝑌^𝑡+1−𝑌^𝑡) +(1−𝛽) ⋅𝑇𝑡T^t+1 =β⋅(Y^t+1−Y^t) +(1−β) ⋅Tt donde 𝛽β es el factor de suavización para la tendencia. 3. Suavización Exponencial Triple (TES): Definición: Es una extensión de DES que también puede manejar datos con estacionalidad. Componentes: Además de la tendencia, incluye un término para modelar la estacionalidad. Fórmulas: Incluyen términos adicionales para modelar la estacionalidad en la serie de tiempo. 4. Factor de Suavización: Definición: Parámetro que controla el peso asignado a los valores observados en la suavización exponencial. Valor: Suele estar en el rango de 0<𝛼<10<α<1, donde valores más cercanos a 1 dan más peso a los valores más recientes. 5. Inicialización del Modelo: Definición: El proceso de establecer valores iniciales para los componentes del modelo de suavización exponencial. Impacto: Los valores iniciales pueden influir en la precisión de los pronósticos y pueden ser determinados mediante métodos heurísticos o ajuste de parámetros. Problema 5.3.1 Método de cuadrados mínimos En un experimento de una maquina lanzadora de pelotas que a medida que esta en uso la distancia de lanzamiento se reduce de dicho experimento se obtuvieron los siguientes valores de las X (Tiempo en hrs) e Y (Metros alcanzados), se sabe que guardan entre sí una relación lineal. El objetivo es encontrar la línea de mejor ajuste que describe la relación entre x e y utilizando el método de mínimos cuadrados. Esta línea puede ayudar a predecir el valor de y en función de x. Los datos recolectados se muestran en la siguiente tabla: X 1.0 2.0 3.0 4.0 Y 1.4 1.1 0.7 0.1 x y Y calculada con y = -0.43x + 1.9 Desviación 1 1.4 1.47 -0.07 2 1.1 1.047 0.6 3 0.7 0.61 0.09 4 0.1 0.18 -0.8 La suma de las diferencias de la recta y real con la y predicha por la ecuación obtenida es: −0,07 + 0,06 + 0,09 − 0,08 = 0 Es decir, nuestra recta efectivamente compensa los puntos que quedaron por encima con puntos que quedaron por debajo Problema 5.3.2 Método de promedios móviles Aplicar el método de promedios móviles para el pronóstico de ventas de gasolina a partir de la siguiente información: Se considerará el promedio móvil a partir de las tres observaciones más recientes. En este caso se utilizará la siguiente ecuación: Resumen de cálculos para promedios móviles de tres semanas Mes Valores de la serie de Pronostico de i esima tiempo (Miles de galones) semana con promedios móviles 1 17 2 21 3 19 4 23 5 18 (17+21+19) /3 = 19 6 16 (21+19+23) /3 = 20 7 20 (19+23+18) /3 = 20 8 18 19 9 22 18 10 20 20 11 15 20 12 22 19 Los promedios móviles también se pueden construir tomando en cuenta valores adyacentes de las observaciones, por ejemplo: En el caso de determinar el promedio móvil para tres observaciones adyacentes de la tabla anterior, se tiene: Mes Valores de la serie de Pronóstico de i esima tiempo (Miles de galones) semana con promedios móviles 1 17 2 21 (17+21+19) /3 = 19 3 19 21+19+23) /3 = 21 4 23 (19+23+18) /3 = 20 5 18 (23+18+16) /3 = 19 6 16 18 7 20 18 8 18 20 9 22 20 10 20 19 11 15 19 12 22 Problema 5.3.3 Método de suavización exponencial Mes Periodo Demanda Alfa = 0.1 Alfa = 0.5 Alfa = 0.9 Enero 1 1000 Febrero 2 350 1000 1000 1000 Marzo 3 950 935 675 415 Abril 4 975 937 813 897 Mayo 5 2100 941 894 967 Junio 6 750 1057 1497 1987 Julio 7 550 1026 1124 874 Agosto 8 300 978 837 582 Septiembre 9 1200 910 569 328 Octubre 10 1770 939 885 1113 Noviembre 11 1350 1022 1328 1704 Diciembre 12 1230 1055 1339 1385 Enero 13 1073 1285 1246 Mes Periodo Demanda Alfa = 0.1 Alfa = 0.5 Alfa = 0.9 Enero 1 1000 Febrero 2 350 1000 1000 1000 Marzo 3 950 935 675 415 Abril 4 975 937 813 897 Mayo 5 2100 941 894 967 Junio 6 750 1057 1497 1987 Julio 7 550 1026 1124 874 Agosto 8 300 978 837 582 Septiembre 9 1200 910 569 328 Octubre 10 1770 939 885 1113 Noviembre 11 1350 1022 1328 1704 Diciembre 12 Enero 13 1230 1055 1339 1385 1073 1285 1246 Bibliografía: Series de tiempo (2015). Universidad Autónoma de México. Recuperado el día 25 de mayo del 2024. Link: http://www.itve.edu.mx/course/view.php&id=98 Análisis de series de tiempo (2014). Slidshare. Recuperado el día 26 de mayo de 2024. Desde: http://es.slidshare.net/f2721/unidad3analisisdeseriesdetiempo Método de series de tiempo (s/f). Series de Tiempo. Uson.mx. Recuperado el 26 de mayo de 2024, de http://www.estadistica.mat.uson.mx/Material/seriesdetiempo.pdf Mínimos cuadrados (s/f). El método de mínimos cuadrados. Unam.mx. Recuperado el 28 de mayo de 2024, de https://sistemas.fciencias.unam.mx/~erhc/calculo3_20171/derivadas_parciales_direcc ionales_2016_12.pdf Suavización Exponencial Ejercicio. (s/f). Scribd. Recuperado el 27 de mayo de 2024, de https://es.scribd.com/document/454689302/suavizacion-exponencial-ejercicio