- Ninguna Categoria
Estadística: Resumen Completo de Conceptos Clave
Anuncio
DAEZEGO
Estadística
La ESTADÍSTICA es la ciencia de los datos. Implica la recolección, clasificación, síntesis,
organización, análisis e interpretación de dichos datos. Actúa como nexo entre los modelos
matemáticos y los fenómenos reales.
Tipos de Estadística
1-Estadística Descriptiva: es la que se dedica a la organización, síntesis y descripción de
un conjunto de datos.
2-Estadística Inferencial: es la que usa datos de una muestra para inferir algo acerca de
una población
Población y Muestra
La población representa la colección completa de elementos, resultados o individuos de los
que queremos analizar una similar característica. Puede ser finita o infinita.
La muestra es un subconjunto tomado de la población que contiene elementos o resultados
que realmente se observan. A su vez, tenemos dos tipos de muestras:
-Muestra Aleatoria Simple: conjunto de tamaño n extraído de una población en la que
cada elemento que se elige no puede estar influenciado por ninguna condición del
entorno. No garantiza que refleja exactamente a la población de la cual se extrajo
-Muestra de Conveniencia: conjunto de tamaño n extraído de una población en el cada
elemento se elige bajo algún criterio de selección y no de manera aleatoria.
Dos muestras diferentes de la misma población son diferentes entre sí, fenómeno se
conoce como variación del muestreo.
Datos, Variables y Escalas de Medición
-Unidad Experimental: es aquella sobre la que se realiza mediciones o se intenta clasificar
en categorías.
-Dato: es alguna característica que se observa de una unidad experimental.
-Variable: es cualquier característica que varía de una unidad experimental a otra. Una
variable aleatoria es aquella que toma valores de observaciones hechas sobre un conjunto
aleatorio de objetos o individuos.
ESTADÍSTICA
DAEZEGO
Tipos de variables
1~Variables Categóricas: como su nombre lo indica, la variable representa alguna
categoría. Hay dos tipos de variables categóricas:
-Nominales: sus valores no se pueden ordenar.
-Ordinales: sus valores pueden ordenarse.
2~Variables Dicotómicas: surgen en forma de ausencia o presencia de una categoría.
3~Variables Numéricas: toman valores numéricos. Hoy dos tipos de variables numéricas:
-Discretas: surgen por conteo y toman valores enteros
-Continuas: surgen de mediciones efectuadas sobre cada unidad experimental.
Una medición consiste en darle un número o código a las observaciones hechas mediante
alguna escala adecuada, donde una escala es un instrumento de medición.
Dependiendo del tipo de variable se emplean diferentes escalas de medición:
Variables Categóricas
Variables Numéricas
Escala Nominal
Escala de Intervalo (DyC)
Escala Ordinal
Escala de Razón (DyC)
ESTADÍSTICA
DAEZEGO
Distribución de frecuencias
Una tabla de distribución de frecuencia nos sirve para organizar los datos y presentarlos de
manera más útil, y así poder obtener cierta información que no se vería tan fácilmente si los
datos no estuviesen ordenados.
Según con el tipo de dato que estemos trabajando podremos realizar distintos tipos de tabla
distribuciones de frecuencia. En esta tabla aparecerán distintos tipos de frecuencias, entre
las cuales tenemos:
-Frecuencia Absoluta f: número de veces que se repite un dato. Se verifica Σf = n
-Frecuencia Relativa fr: proporción de veces que ocurre un dato. Se verifica Σfr = 1
-Distribución de frecuencias para datos categóricos
Es una tabla que asocia a cada categoría de la variable con el número de veces que se repite
dicha categoría. Entonces en esta tabla tenemos la frecuencia absoluta y la frecuencia
relativa. En la primera columna se coloca la identificación, en la segunda columna las
categorías, en la tercera las frecuencias absolutas y en la cuarta las frecuencias relativas:
Id
1
2
3
4
Categoría
Categoría 1
Categoría 2
Categoría 3
Categoría 4
f
5
2
3
2
fr
5/12
2/12
3/12
2/12
f
Para representar estas distribuciones de frecuencia de manera gráfica se usan gráficos de
barras, donde la base de cada barra representa una categoría y la altura de la barra
representa la frecuencia absoluta en la escala adoptada de medida.
6
5
4
3
2
1
0
Categoría 1
Categoría 2
Categoría 3
Categoría 4
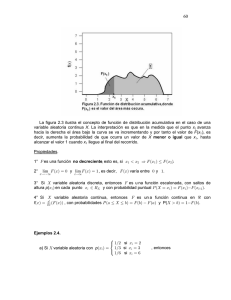
En la gráfica observamos que tenemos 4 categorías diferentes. La primera tiene una
frecuencia de 5, la segunda y la cuarta categoría tienen una frecuencia de 2 y la tercera
categoría tiene una frecuencia de 3.
ESTADÍSTICA
DAEZEGO
-Distribución de frecuencias para datos numéricos
Es una tabla que asocia cada valor que toma la variable numérica con la cantidad de veces
que se repite dicho valor. Así en esta tabla obviamente aparecen nuevamente las
frecuencias absolutas y relativas. Para los datos numéricos podemos agregar dos tipos de
frecuencias mas que son las frecuencias acumuladas:
-Frecuencia Absoluta Acumuladas F: es la suma de las frecuencias absolutas de los valores
menores o iguales al valor que se está considerando. Por supuesto que en al ultimo valor de
la tabla le corresponde un valor de F = n.
-Frecuencia Relativa Acumulada Fr: es la suma de las frecuencias relativas de los valores
menores o iguales al valor que se está considerando. Por supuesto que en al ultimo valor de
la tabla le corresponde un valor de Fr = 1.
Por lo tanto nuestra tabla de distribución de frecuencias tendrá 6 columnas ahora, ya que
debemos agregar estas 2 frecuencias.
Id Valor f
fr
F
Fr
8
2 2/16 2 2/16
1
9
3 3/16 5 5/16
2
10
6 6/16 11 11/16
3
11
4 4/16 15 15/16
4
12
1 1/16 16
1
5
f
En este caso empleamos gráficos de bastones para representar los datos agrupados.
Entonces sería:
7
6
5
4
3
2
1
0
8
9
10
11
Valor
ESTADÍSTICA
12
DAEZEGO
Otra manera de agrupar los datos numéricos es mediante una tabla de frecuencias en las que
se agrupan las observaciones en intervalos llamados intervalos de clase, que no es más que
el rango de valores en que se ha decido agrupar parcialmente los datos. Se define el rango
como la diferencia entre el valor máximo y el mínimo que toma la variable. También, la
cantidad de datos que quedan comprendidos dentro del intervalo representa la f del
intervalo. Para determinar la cantidad de intervalos, k, más adecuada para nuestro conjunto
de datos podemos emplear dos ecuaciones:
Sturges
k=1+
Raíz de n
k= √
( )
( )
Definimos la amplitud de cada intervalo, h, como el cociente entre el rango del conjunto de
datos y la cantidad de intervalos k
=
La marca de clase Mc es el punto medio del intervalo de clase, es decir, es la suma de los
extremos del intervalo dividida 2:
Mc =
ESTADÍSTICA
DAEZEGO
Medidas de Tendencia Central
Son promedios, un valor típico de un conjunto de datos. Las tres que más usaremos son la
media aritmética o valor esperado , la mediana Me y el modo Mo, cuyos cálculos
depende de cómo están presentados los datos.
es la suma de todos los datos dividida entre el total de datos n.
Me es el valor que divide a la mitad la cantidad de datos presentes.
Mo es el valor que más se repite o tiene mayor frecuencia.
-Para datos numéricos sin agrupar
=
∑
(
( / )
" #
Me =
! !
)
! !
! !
! !
-Para datos numéricos agrupados en tabla simple de frecuencia
=
∑
∗
(
( / )
" #
Me =
& !
)
& !
'
'
! !
! !
! !
! !
-Para datos numéricos agrupados en intervalos de clases
=
∑ (' ∗
( =
+
;
=
(
!
!
*+
'
)∗
!
(
a = extremo inferior de la clase Me
( =
+
∗
∗
a = extremo inferior clase modal
f1 = f anterior clase modal
f2 = f posterior clase modal
-Para datos categóricos ordinales
Posición Me =
/ 0
.0
,
3
→2
2
2
'ó =
'ó
'ó
=
=
ESTADÍSTICA
+
DAEZEGO
Medidas de Dispersión
Nos dan idea de la separación de los valores de una variable alrededor de su media
aritmética. Las más usuales son la varianza y el desvío estándar.
La varianza mide el grado de dispersión de los valores con respecto a su X. Si es
2
poblacional se representa con la letra σ y si es muestral con la letra S2.
El desvío estándar es la raíz de la varianza medida en las unidades del conjunto de datos. Si
es poblacional será σ y si es muestral S.
5 =
5= 7
∑( * 6)
∑( * 6)
-Para datos sin agrupar
8 =
∑( * )
*
-Para datos agrupados en intervalos de clases
8 =
∑((' * ) ∗
*
8= 7
∑( * )
8= 7
∑((' * ) ∗
*
*
Notar que para el cálculo de las varianzas y desvíos muestrales se divide por n-1 y no por
n. Esto es porque estamos trabajando con estadísticos (S2 y S)
Coeficiente de Variación (cv)
Se usa para comparar las dispersiones de dos ó más distribuciones, cuyas observaciones
han sido medidas con escalas de razón únicamente. Se define como el cociente entre la
varianza muestral y la media aritmética:
Variables Tipificadas
'9 =
8
Mide la desviación respecto de la X en unidades de la S. Es adimensional y viene dada:
:=
*
8
ESTADÍSTICA
DAEZEGO
Medidas de Asimetría
Nos permiten apreciar la simetría o asimetría de una distribución dada. El modo es la
referencia central. Según estas medidas una distribución puede ser normal, sesgada a la
derecha o sesgada a la izquierda.
Normal:
= Me = Mo
Sesgada a la derecha: La
Sesgada a la izquierda: La
se ubica a la derecha de Mo y Me entre ellos.
se ubica a la izquierda de Mo y Me entre ellos.
Sesgada a la derecha o asimetría positiva
Sesgada a la izquierda o asimetría negativa
Medidas de Apuntamiento o Curtosis
Nos permite apreciar si una distribución es más o menos apuntada que la distribución
normal. Estas medidas se refieren a la diferencia de los valores centrales de la variable.
ESTADÍSTICA
DAEZEGO
Medidas de Orden
Aquí aparece el concepto de cuantiles que son valores que dividen al conjunto de datos en
partes iguales. Entonces podemos nombrar los siguientes:
-Cuartiles: cuando se divide el conjunto ordenado de datos en 4 partes iguales.
-Octiles: cuando se divide el conjunto ordenado de datos en 8 partes iguales.
-Deciles: cuando se divide el conjunto ordenado de datos en 10 partes iguales.
-Percentiles: cuando se divide el conjunto ordenado de datos en 100 partes iguales.
Para nuestro estudio emplearemos los Cuartiles, así que veremos como se calculan sus
posiciones y sus respectivos valores:
Las posiciones las indicaremos con letras minúsculas q y los valores de los Cuartiles los
indicaremos con letras mayúsculas Q.
Q1 = Xq1
Q2 = Me
Q3 = Xq3
;1 =
(= >)
;3 =
A(= >)
?
?
ESTADÍSTICA
DAEZEGO
Probabilidad
Este término se usa generalmente para indicar que hay cierta incertidumbre sobre algo que
ya ocurrió, que está ocurriendo o que ocurrirá en el futuro.
Para realizar el estudio de la probabilidad debemos definir algunos conceptos básicos que
son:
-
Experimento: describe cualquier proceso que genere datos iniciales
Experimento Aleatorio: se genere bajo un conjunto de reglas, puede repetirse y el
resultado de cada ejecución depende de la casualidad
Espacio Muestral (S o Ω): representa el conjunto de todos los resultados posibles
de un experimento.
S = {C, X}
;
donde C= número de caras y X = número de cruces
S = {x/x es una ciudad con población mayor a 1 millón}
S = {(x, y)/ x2 + 4y ≤ 10}
-
Elemento o Punto Muestral: es cada resultado del espacio muestral.
Evento: es un subconjunto o parte de un espacio muestral.
Evento simple: es un subconjunto que tiene un solo elemento.
Evento compuesto: es aquel que puede expresarse como la unión de eventos
simples, en otras palabras es un subconjunto del espacio muestral que tiene más de
un elemento.
Los eventos, ya sean simples o compuestos se suelen representar con letras mayúsculas
distintas de S, por ejemplo:
Sea S={1,3,5,7,9,11}
A={7} ; B={3, 9, 11}
Sea S={{C, X} x {C, X} x {C, X}}
C={C,C,X} ; D={(C, X,C) , (X, C,C)}
ESTADÍSTICA
DAEZEGO
Técnicas de Numeración
-
Principio de Multiplicación
Supongamos que un determinado procedimiento, llamado A, puede ocurrir de nA maneras.
Ahora tenemos un segundo procedimiento, B, que puede ocurrir de nB maneras y que a su
vez cada manera de efectuar A puede ser seguida de la manera de efectuar B. Entonces el
procedimiento conjunto entre A y B puede efectuarse de (nA* nB) maneras.
-
Principio de Adición
Supongamos que un determinado procedimiento, llamado A que puede ocurrir de nA y otro
procedimiento B que puede ocurrir de nB maneras. Además no pueden ocurrir juntos dichos
procedimientos, entonces el número de maneras como se puede efectuar A ó B es nA + nB
-
Permutaciones
Pn = n!
-
Combinaciones
C(n, x) =
=
!
! ∗ ( * )!
Probabilidad de un evento
A continuación se veremos las teorías de probabilidad:
-
Teoría Clásica
Teoría de Frecuencias Relativas
Teoría Axiomática
Teoría Personalista o Subjetiva
Teoría Clásica
Si un experimento puede producir cualquiera de los n resultados igualmente probables y si
exactamente nA de esos resultados pertenecen al evento A, entonces la probabilidad del
C
evento A será:
2(C) =
0 ≤ nA≤n
0≤ 2(C) ≤1
Teoría de Frecuencias Relativas
Si un suceso puede ocurrir de n maneras mutuamente excluyentes e igualmente probables y
nA es el número de veces que ocurre un suceso A, entonces:
2(C) =
C
ESTADÍSTICA
DAEZEGO
-Muestreo con reemplazo o con sustitución
De una muestra se extrae un elemento para estudiarlo y luego se lo devuelve al total de la
muestra para así poder extraer otro.
-Muestreo sin reemplazo o sin sustitución
De una muestra se extrae un elemento para estudiarlo y no se lo devuelve al total de la
muestra para así extraer el segundo.
Teoría Axiomática
Dado un experimento aleatorio descripto por el espacio muestral S, la probabilidad es una
función P( ) que asigna a cada evento un número real no negativo indicado como P(E) que
sería la probabilidad del evento E:
P(E) : S
R+0
Las tres propiedades de la función de probabilidad son:
1- P(E) ≥ 0 VE
2- P(S) = 1
3- P(E U F) = P(E) + P(F) si (E ∩ F) = Φ ; Φ = conjunto vacío
Definición: La probabilidad de un evento A es la suma de todos los puntos muestrales de A
Teoremas Importantes Sobre Probabilidad
1- P(Φ) = 0
2- Sea Ac el complemento de A, entonces
P(Ac) = 1 – P(A)
3- Si A y B son dos sucesos cualesquiera, entonces
P(A U B) = P(A) + P(B) – P(A∩B)
4- Sean A, B y C sucesos cualesquiera, entonces
P(AUBUC) = P(A) + P(B) + P(C) – P(A∩B) – P(A∩C) – P(B∩C) + P(A∩B∩C)
5- Si A B entonces P(A) ≤ P(B)
6- Si A B entonces P(B – A) = P(B) – P(A)
ESTADÍSTICA
DAEZEGO
Probabilidades Marginal, Conjunta y Condicionada
Probabilidad Marginal
Si un evento E puede producir cualquiera de los n resultados igualmente probables y si
exactamente nE de estos resultados pertenecen al evento E, entonces definimos la
probabilidad marginal de E así:
D
P(E) =
Probabilidad Conjunta
( C ∩ F)
Dados dos sucesos A y B de S, la probabilidad de ocurrencia de A y B simultáneamente la
P(A∩B) =
denominamos probabilidad conjunta:
Probabilidad Condicionada
P(C⁄F) =
2(C∩F)
Dados dos sucesos A y B de S con P(B) ≠ 0, la probabilidad de ocurrencia de A dado que
ocurrió B es:
Ley Multiplicativa de Probabilidad
P(C⁄F) =
2(C∩F)
2(F)
→
2(F)
P(A∩B) = P(B) . P(C⁄F)
P(A∩B∩C) = P(A) . P(F⁄C) . P( ⁄C ∩ F)
Dos sucesos A y B son independientes si y sólo si la probabilidad conjunta es igual al
producto de las probabilidades marginales.
Dos sucesos A y B son independientes si y sólo si la ocurrencia de A no influye en la
probabilidad de ocurrencia de B.
Regla de Bayes
P(A/B) =
2(C∩F)
2(F)
=∑
2(C∩F)
2(C∩F)
=
ESTADÍSTICA
2(C).2(F⁄C)
∑ 2(C).2(F⁄C)
DAEZEGO
Variables Aleatorias y Distribución de Probabilidades
La función cuyo valor es un número real determinado por cada elemento en el espacio
muestral se llama variable aleatoria
Si un S contiene una cantidad finita de posibilidades o una secuencia interminable con
tantos elementos como el total de números enteros, dicho S se llama espacio muestral
discreto y a la variable aleatoria definida en dicho espacio se la llama variable aleatoria
discreta
Si un S contiene un número infinito de posibilidades igual al número de puntos en un
segmento de recta, dicho S se llama espacio muestral continuo y la variable aleatoria
correspondiente a dicho S variable aleatoria continua
La función f(xi) = P(X = xi) es una función de probabilidad de la variable aleatoria discreta
X si para cada xi ϵ Rx , donde Rx = resultados posibles o recorrido, si se cumple que:
1- f(x) ≥ 0
→
2- ∑ ( ) =
→
3- P(X = x) = f(x)
f(x) es función de probabilidad de la variable aleatoria X
(x, f(x)) distribución de la variable aleatoria X
Así decimos que f(x) es una función de masa o cuantía cuando X es una variable
aleatoria discreta.
La función f(x) es una función de probabilidad de la variable aleatoria continua X definida
sobre un conjunto de números reales si:
123-
f(x) ≥ 0 →
J
I*J ( )! =
P(a < X < b) = I
K
f(x) es función de probabilidad de la variable aleatoria X
→
(x, f(x)) distribución de la variable aleatoria X
( )!
Así decimos que f(x) es una función de densidad cuando X es una variable aleatoria
continua.
Función de Probabilidad Acumulativa
La distribución acumulativa F(x) de una variable aleatoria discreta X con función de
cuantía f(x) viene dada por:
+ ( ) = ∑∀
M
( )
ESTADÍSTICA
DAEZEGO
La distribución acumulativa F(x) de una variable aleatoria continua X con función de
densidad f(x) está dada por:
+( ) = I*J ( )!
Además se tiene que ( ) =
Propiedades:
; Se reemplazó f(x) por f(t) para no confundir las variables
!+( )
!
si existe la deriva, entonces podemos escribir:
2( < O < P) = +(K) − +( )
+(−∞) = S
+(∞) =
∀
≤ K ∶ +( ) ≤ +(K)
Media y Varianza Poblacionales de una Variable Aleatoria
Sea X una variable aleatoria con distribución de probabilidad f(x), el valor esperado o
esperanza matemática, o media de la población de X es:
DV W =
/X . ( )
- ∀
J
.
-Y
,*J
9. . ! '
. ( )
9. . '
Sea X una variable aleatoria con distribución de probabilidad f(x), la varianza o variancia
de X es:
ZV W =
/ X( − DV W)
- ∀
J
.
- Y ( − DV W)
,*J
( ) = DV
( ) ! = DV
W − (DV W)
W − (DV W)
9. . ! '
9. . '
Entonces la variable aleatoria, discreta o continua, se distribuye con una función de
parámetros E[X] y V[X]:
~ (DV W, ZV W)
Sean dos variables aleatorias X e Y con medias E[X] y E[Y], la covarianza vale:
' 9V , ]W = DV ]W − DV W . DV]W
Si X e Y son variables independientes entonces la covarianza vale cero, lo contrario no
es cierto.
ESTADÍSTICA
DAEZEGO
:=
*DV W
Supongamos que tenemos una variable aleatoria X ~ g (E[X], V[X]) y queremos emplear la
variable z que se define como sigue:
^ZV W
Ahora necesitamos saber como se distribuye esta variable z, es decir, con que esperanza y
con que varianza. Entonces hacemos lo siguiente:
DV:W = E `
ZV:W = V j
Entonces
d=
a*bVaW
^cVaW
X − EVXW
^VVXW
>
^cVaW
k=
eEfX − EVXWgh =
>
^cVaW
(EVXW − EVXW) = S
1
1
VfX − EVXWg =
VVXW =
VVXW
VVXW
z ~ g (0, 1)
Variable Aleatoria Bidimensional
Tomemos el caso en que tenemos un espacio muestral con dos variables definidas X e Y.
La distribución o función de ocurrencia conjunta es: f(x, y) = P(X = x, Y = y)
Así, f(x, y) proporciona la probabilidad de que los dos resultados ocurran al mismo
tiempo.
La función f(x, y) es una distribución de probabilidad conjunta de las variables aleatorias X
e Y si se cumple que:
( , l) ≥ S ∀( , l)
2- ∑ ∑l ( , l) =
1-
o
I Il
3- 2V( , ]) ∈ CW = ∑ ∑C ( , l)
Para cualquier región A del plano xy.
( , l)! !l =
o
2V( , ]) ∈ CW ∬C ( , l)! !l
Sean X e Y dos variables aleatorias, discretas o continuas, con distribución de probabilidad
conjunta f(x, y) y las distribuciones marginales g(x) y h(y). Decimos que dichas variables
son independientes si y sólo si:
( , l) =
( ) ∙ (l)
ESTADÍSTICA
∀(r, s)
DAEZEGO
Distribuciones Discretas
Si un S contiene una cantidad finita de posibilidades o una secuencia interminable con
tantos elementos como el total de números enteros, dicho S se llama espacio muestral
discreto y a la variable aleatoria definida en dicho espacio se la llama variable aleatoria
discreta.
Distribución Binomial
Es una de las distribuciones de probabilidad más útiles, se la emplea por ejemplo en control
de calidad, producción, investigación, etc. Tiene que ver con el experimento aleatorio que
produce en cada ensayo o prueba uno de dos resultados posibles mutuamente excluyentes:
ocurrencia de un criterio o característica específico, que llamamos éxito, y no ocurrencia de
éste que llamamos fracaso. Los términos de "éxito y fracaso" son solo etiquetas y su
interpretación puede no corresponder con el resultado positivo o negativo de un
experimento en la realidad.
El experimento aleatorio consiste en n ensayos repetidos e idénticos. Son ensayos con
reposición. Cada uno de los n ensayos arroja sólo uno de los dos resultados posibles, es
decir éxito ó fracaso. La probabilidad de éxito u ocurrencia, denominada p, permanece
constante para cada ensayo. La probabilidad de fracaso se denota q= 1-p Cada ensayo se
repite en idénticas condiciones y es independiente de los demás.
Así no interesa encontrar la probabilidad de obtener x número de éxitos al realizar n
ensayos. Entonces la función de probabilidad de X será:
( ) = 2( = ) = K( , , ) = 3
" #
S
t
= S, , , … . ,
*
con n entero y 0 ≤ p ≤ 1
Veamos como se distribuye una variable X binomial
DV W =
~ K( , , ) v
ZV W =
ESTADÍSTICA
t
DAEZEGO
Distribución Geométrica
Consideramos un experimento donde tiramos una moneda las veces que sea necesario hasta
obtener la primera cruz, donde la probabilidad de obtener una cruz es p. Entonces, cuántos
tiros debemos realizar.
Sea X el número de tiros, así
P (X = 1) = p
P (X = 2) = (1 − p)p
P (X = 3) = (1 − p)2 p
Entonces de manera general es
P (X = x) = (1 − p)x−1p
La distribución de X es la que llamamos distribución geométrica. Ahora podemos dar una
definición mas copada:
Si la probabilidad de éxito en cada ensayo es p, entonces la probabilidad de que
x ensayos sean necesarios para obtener un éxito es:
2( = ) = ( − )
w ~ x(r, y)
Distribución Hipergeométrica
*
∙
zVwW =
= t
{y
*
}
|VwW = {
y
∙
Esta distribución la vamos a emplear cuando tenemos muchos datos. El experimento
hipergeométrico es la probabilidad de seleccionar x éxitos entre los k artículos
denominados éxitos y los n-x fracasos entre los N-k artículos llamados fracasos, cuando se
selecciona una muestra de tamaño n entre los N artículos. La muestra se toma sin
reposición, es decir que es dependiente.
e€rhe•*€
h
*r
r = S, , , … ,
•
~(r, •, , €) = • e h
S
ESTADÍSTICA
( , €)
‚ƒ„‚ …†x‡„
DAEZEGO
~
, ˆ, ,
•
DV W
ZV W
ˆQ
‰ Q Š‰
Š
ˆ
ˆ ˆQ
donde eˆ* h es el factor de correlación
ˆ*
Distribución de Poisson
ˆ
ˆQ
t‰
Š
ˆQ
Los experimentos que proporcionan valores numéricos de una variable aleatoria X, el
número de éxitos que ocurren durante un intervalo de tiempo dado se llama experimento de
Poisson.
En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de
probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la
probabilidad que ocurra un determinado número de eventos durante cierto periodo de
tiempo.
La distribución de Poisson es el caso límite de la distribución binomial. De hecho, si los
parámetros n y θ de una distribución binomial tienden a infinito y a cero de manera
que
se mantenga constante, la distribución límite obtenida es de Poisson.
Como consecuencia del teorema central del límite, para valores grandes de λ, una variable
aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente
converge a una distribución normal de media nula y varianza 1.
2
,‹
*‹
∙ ‹
!
S
S, , , … , ∞
Donde λ es el promedio de éxitos que ocurre en un intervalo de tiempo o en una región
dada.
ESTADÍSTICA
DAEZEGO
DISTRIBUCIONES CONTINUAS
DISTRIBUCIÓN RECTANGULAR o UNIFORME
En esta distribución continua, todos los intervalos de igual longitud en la distribución en su
rango son igualmente probables. El dominio está definido por dos parámetros, a y b, que
son sus valores mínimo y máximo. La distribución suele escribirse en forma abreviada
como U(a,b). Su función de densidad es:
Los valores en los dos extremos a y b no son por lo general importantes porque no
afectan el valor de las integrales de f(x) dx sobre el intervalo, ni de x f(x) dx o
expresiones similares. Veamos como se distribuye una variable aleatoria con esta
función de densidad
DV W
ZV W
K
Y
KQ
DV
!
W Q DV W
KQ
K)
KQ
DISTRIBUCIÓN EXPONENCIAL
Esta distribución tiene un parámetro λ > 0 cuya función de densidad es:
El valor esperado y la varianza de una variable aleatoria X con distribución exponencial
son:
DV W
ZV W
‹
‹
ESTADÍSTICA
DAEZEGO
DISTRIBUCIÓN NORMAL
La distribución de una variable normal queda perfectamente definida por dos parámetros
que son su media µ y su desviación estándar σ. Entonces se dice que una variable
aleatoria continua X sigue una distribución normal de parámetros µ y σ si su función de
densidad está dada por:
Se llama distribución normal "estándar" a aquélla en la que sus parámetros toman los
valores µ = 0 y σ = 1. En este caso la función de densidad tiene la siguiente expresión:
Para el cálculo de los valores de su distribución se emplean tablas.
Debido a que la curva alcanza su mayor altura en torno a la media, mientras que sus colas
se extienden asintóticamente hacia los ejes, cuando una variable siga una distribución
normal, será mucho más probable observar un dato cercano al valor medio que uno que se
encuentre muy alejado de éste.
Propiedades de la distribución normal:
La distribución normal posee ciertas propiedades importantes que conviene destacar:
123-
4-
5-
6-
Tiene un único modo, el cual coincide con su media y su mediana.
La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre
y
es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
Es simétrica con respecto a su media. Entonces, para este tipo de variables existe
una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de
observar un dato menor.
La distancia entre la línea trazada en la media y el punto de inflexión de la curva es
igual a una desviación típica. Cuanto mayor sea la desviación estándar, más
aplanada será la curva.
El área bajo la curva comprendida entre los valores situados aproximadamente a dos
desviaciones estándar de la media es igual a 0.95. En concreto, existe un 95% de
posibilidades de observar un valor comprendido en el
intervalo
.
La forma de la campana de Gauss depende de los parámetros. La media indica la
posición de la campana, de modo que para diferentes valores de media la gráfica es
desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar
determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de
,
más se dispersarán los datos en torno a la media y la curva será más plana. Un valor
ESTADÍSTICA
DAEZEGO
pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos
cercanos al valor medio de la distribución.
Así podemos notar que no existe una única distribución normal, sino una familia de
distribuciones con una forma común, diferenciadas por los valores de su media y su
varianza. De entre todas ellas, la más utilizada es la distribución normal estándar, que
corresponde a una distribución de media 0 y varianza 1, entonces resulta:
Es importante tener en cuenta que a partir de cualquier variable X que siga una
distribución normal, se puede obtener otra característica Z con una distribución normal
estándar realizando la siguiente transformación:
Así, la variable z se distribuye normal, con esperanza 0 y varianza 1. Esta propiedad resulta
especialmente interesante en la práctica, ya que para una distribución Œ 0, 1 existen tablas
a partir de las que se puede obtener de modo sencillo la probabilidad de observar un dato
menor o igual a un cierto valor z, y que permitirán resolver preguntas de probabilidad
acerca del comportamiento de variables de las que se sabe o se asume que siguen una
distribución aproximadamente normal.
Propiedad reproductiva de la distribución normal
Sean dos distribuciones normales, con variables aleatorias independientes
] ~ ˆ 6l , 5l . Si M = X + Y entonces:
(~ ˆ 6 ) 6] , 5 ) 5l
~ˆ 6 ,5
e
Es decir que según esta propiedad podemos sumar algebraicamente las variables aleatorias
independientes para formar otra. Cabe aclarar que en dicha suma los coeficientes que
multiplican a las variables no necesariamente deben ser 1, sino que pueden tomar otros
valores inclusive negativos.
ESTADÍSTICA
DAEZEGO
APROXIMACIÓN DE LA BINOMIAL MEDIANTE LA NORMAL
Podremos realizar esta aproximación bajo ciertas condiciones que son:
1- n es grande y S,
≤
2- n cualquiera y p = 0,5
≤ S, Ž
Entonces, si se da alguna de las dos condiciones mencionadas se puede realizar la
aproximación de la variable binomial mediante una variable normal. Así podemos enunciar
el siguiente teorema:
Si X es una variable aleatoria binomial, con media np y varianza npq, la forma límite de
w* y
la distribución de • = y} cuando → ∞, es la distribución normal estándar •(•, S, )
^
Distribución Gamma
La variable aleatoria continua X tiene una distribución Gamma con parámetros n y β si su
función de densidad es:
( )=
•
•
‘
‘ ’( )
> 0, ” > 0 • – > 0
Para cuando β=1 la distribución gamma tiene esperanza E[X] = nβ y varianza V[X] = nβ2
ESTADÍSTICA
DAEZEGO
Distribución CHI-CUADRADA ( χ2)
La variable aleatoria X tiene una distribución Chi-Cuadrada, con n grados de libertad, si su
función de densidad es:
•
~ —(
)
’
•
x>0
" #
, y además DV W =
l ZV W =
Propiedad reproductiva de la CHI-CUADRADA
Sean X1, X2,…,Xn variables aleatorias independientes con distribución χ2 se tiene que:
]=
~—(
)
+
Distribución t de Student
~—(
)
+ ⋯+
~—(
)
∴ ] ~ —(∑
)
Si ~ ˆ(S, ) e ] ~ —( ) siendo ambas variables aleatorias independientes, entonces la
variable aleatoria
=
^]⁄
tiene una distribución “t” con n grados de libertad. Su
función de densidad es:
( )=
’V(
)/ W
√ š ’( / )
" + #
Esta distribución tiene E[X] = 0 y ZV W =
*
*
>0
ESTADÍSTICA
−∞ < › < ∞
DAEZEGO
Distribución “F” de Fisher
Ÿ
Ÿ
Si œ> ~ •(=
e œŸ ~ •(=
) que son ambas variables aleatorias independientes, entonces la
ž)
variable aleatoria + =
]{
]{
, que resulta del cociente de cada Chi-cuadrada divida por sus
grados de libertad, tiene una distribución F con n1 y n2 grados de libertad. Su función de
densidad es:
(+) =
’¡
’e
(
h ’e
)
¢‰
h¡
Š +
+
"
¢
(
• #
~ +(
)
ESTADÍSTICA
,
)
DAEZEGO
Teoría de Muestras
La teoría del muestreo es el estudio de las relaciones existente entre una población y las
muestras extraídas de la misma. Tiene gran interés en muchos aspectos de la estadística.
Por ejemplo permite estimar cantidades desconocidas de la población a partir del
conocimiento de las correspondientes cantidades muestrales. Las cantidades poblacionales
se conocen comúnmente como parámetros, mientras que las cantidades muestrales
reciben el nombre de estadísticos.
La teoría de muestreo es también útil para determinar si las diferencias que se puedan
observar entre dos muestras son debidas a la aleatoriedad de las mismas o si por el contrario
son solamente significativas.
Entonces en esta parte de nuestro estudio nos fijaremos en los distintos tipos de muestras y
las variables aleatorias asociadas a cada una de ellas.
Para seleccionar una muestra aleatoria de tamaño n de una población f(x), debe definirse
una variable aleatoria Xi, con i = 1, 2, …, n. Las variables Xi formarán así una muestra
aleatoria de la población f(x) con valores numéricos xi si dichas variables son
independientes cada una con la misma distribución de probabilidad f(x). Entonces su
)= (
) (
distribución de probabilidad conjunta se expresa como:
,
,…,
)… (
)
La función conjunta resulta ser el producto de las funciones marginales
Dijimos que una cantidad muestral se llama estadístico, así que vamos a dar una definición
del mismo. Decimos que cualquier valor calculado a partir de una muestra se llama
estadístico, o también que un estadístico es una variable aleatoria que depende sólo de la
muestra aleatoria observada. Algunos estadísticos importantes de una muestra de tamaño
n son la media muestral
y la varianza muestral S2.
Así, la distribución de probabilidad de un estadístico recibe el nombre de distribución
muestral.
A continuación veremos como se distribuyen los estadísticos más empleados para nuestro
estudio.
ESTADÍSTICA
DAEZEGO
Distribución de Medias
∑
Sea X1, X2,…, Xn una muestra aleatoria con media
entonces veamos como se
distribuye
DV W
ZV W
D¡
∑
|¡
∑
¢
¢
∑ DV W
∑ ZV W
DV W ∑
ZV W ∑
DV W Es decir que DV W
DV W
ZV W Es decir que ZV W
ZV W
Teorema central del límite
Si
es la media de una muestra aleatoria de tamaño n tomada de una población con media
µ y varianza σ2, entonces la forma límite de la distribución •
distribución estandarizada ˆ(S, )
*6
5
{
√
cuando
→ ∞, es la
Para poder realizar esta estandarización de la £ y emplear la variable z es necesario conocer
los parámetros µ y σ2, así como el tamaño de la muestra.
Supongamos ahora el caso en que sólo conocemos µ y n. Por dicho motivo no podremos
emplear el teorema central del límite ya que no conocemos σ2. Entonces recurrimos a la
distribución “t” de Student cuando el tamaño de la muestra n < 30:
Entonces recordando que la t resulta del cociente de una normal estándar y una chi sobre
sus grados de libertad, ¤ =
ˆ(S, )
7—(9) ⁄9
¤=
~
¥,(9),
−6
5⁄√
resulta que:
( − )8
¦
5 ( − )
=
− 6
8⁄√
~
¥,( * )
Se distribuye con (n-1) grados de libertad. Esto es debido a que se trabaja con un
estadístico que es S2, si hubiésemos empleado un estadístico más serían (n-2) grados de
libertad y así sucesivamente.
Para el caso en que n > 30 se tiene que 5 → 8
∴
ESTADÍSTICA
:=8
*6
{
√
~ ˆ(S, )
DAEZEGO
Distribución de Varianzas
Si S2 es la varianza de una muestra aleatoria de tamaño n extraída de una población con
varianza σ2, entonces la variable aleatoria §
Ÿ
tiene una distribución •ª,(=*>)
.
=*> ¨
©
Entonces para la varianza empleamos la distribución Chi- Cuadrada.
Si S>Ÿ y SŸŸ son las varianzas de dos muestras aleatoria independiente de tamaño n1 y n2
Distribución de cociente de varianzas
respectivamente extraídas de poblaciones normales con varianzas σ>Ÿ y σŸŸ , entonces
¯>Ÿ ⁄°>Ÿ
¯>Ÿ °ŸŸ
=
~ ®ª,(±ž,±
¯ŸŸ ⁄°ŸŸ
¯ŸŸ °>Ÿ
®=
)
El cociente de varianzas tiene una distribución F con v1 y v2 grados de libertad. Para
construir esta la variable aleatoria F se parte de realizar el cociente entre dos poblaciones
normales con distribución Chi-Cuadrada dividida cada una por sus grados de libertad.
Distribución de Diferencia de Medias
Supongamos que tenemos dos poblaciones que pueden ser normales o no, y queremos saber
como se distribuye la diferencia de medias. En esta situación se pueden presentar diferentes
casos en los que se emplearan diferentes distribuciones.
Caso1: Varianzas poblacionales conocidas
1- Poblaciones normales
Entonces tenemos dos poblaciones normales de las cuales conocemos sus varianzas
σ>Ÿ y σŸŸ , y extraemos una muestra n1 y n2 respectivamente:
X> ~N "μ> ,
´ž
µž
Por lo tanto
#
y X Ÿ ~N "μŸ ,
´
µ
#
−
−
~ ˆ(DV
~ ˆ "6 − 6 ,
ESTADÍSTICA
5
+
5
−
#
W, ZV
−
W)
DAEZEGO
Entonces podemos emplear la variable aleatoria z siguiendo el teorema central del límite:
:
*
¦
5
~ ˆ(S, )
* 6 *6
5
2- Poblaciones no normales
En el caso de que estemos tratando con poblaciones no normales pero el tamaño de las
muestras es superior a 30, entonces podemos emplear la variable aleatoria z definida
anteriormente:
> 30 → ¶ =
(
*
)* (6 *6 )
5
¦
5
~ ˆ(S, )
Caso 2: Varianzas poblacionales desconocidas
1- Poblaciones normales.
En esta situación suponemos que las varianzas poblacionales son iguales σŸ = σ>Ÿ = σŸŸ y
deberemos emplear una variable aleatoria t cuya distribución se compone del cociente entre
una Normal Estándar y la raíz de una Chi-Cuadrada dividida entre sus grados de libertad, es
decir: ¤ =
ˆ(S, )
7—(9) ⁄9
~
¥,(9),
El resultado de realizar las operaciones pertinentes nos da la siguiente forma para la
diferencia de medias:
¤=
(
*
)* (6 *6 )
8' 7
~
¥,(
* )
donde 8' = 7
(
* )8
(
(
* )8
* )
2- Poblaciones no normales
Al igual como se mencionó antes, para tamaños de muestras superiores a 30 podemos
emplear la variable aleatoria z según la siguiente estandarización:
> 30 → ¶ =
(
*
¦
)* (6 *6 )
8
8
ESTADÍSTICA
~ ˆ(S, )
DAEZEGO
Estimación
La teoría de la Estadística Inferencial (o inferencia estadística) se puede definir como
aquellos métodos que permiten hacer inferencia sobre una población. Para ello se eligen
estimadores de manera que el modelo se ajuste lo mejor posible al comportamiento
observado, para luego estudiar a dichos estimadores como variables aleatorias.
Así lo que tratamos de hacer es emplear un determinado estadístico para que nos estime
un determinado parámetro. Generalmente se busca el estadístico que mejor estime a dicho
parámetro. A estos estadísticos los llamamos estimadores.
Estimación Puntual
Supongamos que tenemos un parámetro cualquiera llamado º, entonces un estimador
» es una función de los valores de la muestra y se dice que es
puntual de º, que llamaremos º
puntual porque consiste en un solo valor. Por lo recién dicho tenemos que:
»
º
,
,
¼, … ,
)
»(
º= º
por lo que
».
Queda a la vista que º es función de º
,
,
¼, … ,
)
A modo de ejemplo supongamos que X ~ N(μ, σŸ ), entonces queremos estimar el
parámetro µ mediante el estimador
=
∑
»(
= º
,
,
¼, … ,
)
→
½=
Aquí podemos ver que el estimador es función de los valores de la muestra y que tiene un
solo valor, ya que la media aritmética tiene un solo valor.
Algunos parámetros (como ser µ) poseen más de un estimador ( , ( l ). Entonces
cómo podemos determinar cual es el mejor de todos ellos. Para saber cual es el mejor de
todos ellos, hay que ver cual cumple con las siguientes propiedades:
» es un estimador insesgado del
1- Insesgamiento: Se dice que en estadístico º
»g = º
parámetro º si se verifica que: Dfº
» de º tiene varianza mínima si se
2- Varianza Mínima: Un estimador puntual º
»g < ¾Vº
» W donde º
» es cualquier otro estimador de º.
verifica que |fº
Si hacemos los cálculos para los diferentes estimadores de µ veremos que el que cumple
con las dos propiedades anteriores es .
ESTADÍSTICA
DAEZEGO
Método de Máxima Verosimilitud
Es un método de estimación que nos brinda estimadores asintóticamente insesgados y de
varianza mínima cuando n es grande. Nos brinda estimadores para parámetros de cualquier
distribución que cumplen con las propiedades de los estimadores puntuales. ESTE
MÉTODO SE USA SÓLO CUANDO CONOZCO LA POBLACIÓN.
Dada una muestra aleatoria X1, X2,…, Xn de una población con función de densidad (o
cuantía), f(x, θ) con θ desconocido y además cada una de las variables aleatorias tienen
como función fi(xi, θ):
f x> , xŸ , … , xµ , θ) = f> (x> , θ )fŸ (xŸ , θ ) … fµ (xµ , θ)
(
,
,…,
f(x> , xŸ , … , xµ , θ) = f(x> , θ )f(xŸ , θ ) … f(xµ , θ)
, º) = ∏
( , º ) Función de probabilidad conjunta
» del parámetro º es aquel que
Entonces el estimador de máxima verosimilitud (E.M.V.) º
maximiza la función de probabilidad conjunta (función de verosimilitud). A la función
de verosimilitud la denominamos con la letra L.
Ã=∏
( ,º )
(Ä) = ∑
V ( , º )W ; esto es porque L y ln(L) tienen los mismos puntos críticos
Luego procedemos a encontrar los puntos críticos haciendo:
!V (Ã)W
!º
=S
». Finalmente hallamos la derivada segunda y la evaluamos
De ahí procedemos a despejar º
» y vemos si es un máximo.
en º
ESTADÍSTICA
DAEZEGO
Estimación por Intervalos de Confianza
La estimación por intervalos nos permite conocer con que error estamos trabajando. Para
construir un intervalo lo que hacemos es tomar un valor inferior º y otro valor superior
º tales que la probabilidad de que dichos valores encierren al valor verdadero de º sea
igual a Q ¥, que es el nivel de confianza del intervalo y ¥ es el error que nos podemos
permitir:
2 º <θ<º
Q¥
Variable Fundamental
Una variable aleatoria es una variable fundamental o pivotal si y sólo si:
-
Depende solo del parámetro al cual se le construye el intervalo.
Depende sólo del estimador de máxima verosimilitud.
Debe tener una distribución fija y conocida, la cual no dependa del parámetro
al cual se le construye el intervalo.
Por ejemplo: Sea X ~ N(μ, σŸ ) con σŸ conocida, encontrar la variable pivotal para μ
:=5
*6
{
√
~ˆ(S, )
Intervalo de confianza para la Media
Veremos como se construye un intervalo para la media poblacional µ según sea el caso
que se nos presente.
-
Población Normal con σ2 conocida
La variable pivotal es : = 5
*6
{
√
~ˆ(S, )
El mejor intervalo es el que tiene menor longitud. Para el caso de una distribución
Normal que posee simetría, el intervalo de menor longitud se da cuando los extremos
son iguales en magnitud pero signos opuestos, por lo que para un nivel de confianza
dado resulta:
2(−: < ¶ < : ) = − ¥
2 Å −:
*¥
<5
Los subíndices de : indican la posición
2"
−:
5
*¥ √
*6
{
√
<Ç<
<:
*¥ Æ
+ :
ESTADÍSTICA
=
5
*¥ √
−¥
#=
−¥
DAEZEGO
-
Población Normal con σ2 desconocida
*6
8{
√
La variable pivotal es
~
( * )
Entonces por ser una distribución simétrica los extremos deben tener la misma posición
pero de signo opuesto, así resulta:
2(−
2"
2 Å−
−
*¥
8
*¥ √
<›<
<8
*6
{
√
<Ç<
<
)=
+
*¥ Æ
−¥
=
8
*¥ √
−¥
#=
−¥
Intervalo de Confianza para la Varianza
Una estimación puntual insesgada de la varianza de una población normal está dada por
la varianza muestral S2, es decir que S2 es el estimador de máxima verosimilitud de σ2.
La variable pivotal es • Ÿ =
Ÿ
~ •(=*>)
(=*>)¨
©
En este caso la distribución no es simétrica, por lo que las posiciones de la variable • Ÿ no
son iguales y de signo contrario como ocurría antes.
2 "• Ÿ ¥ < • Ÿ < • Ÿ
2 "• Ÿ ¥ <
2Å
(=*>)¨
(=*>)¨
È
¥
•
©
*¥ #
< •Ÿ
< °Ÿ <
=
*¥ #
(=*>)¨
È ¥
=
−¥
Æ=
−¥
−¥
Intervalo de confianza para Proporciones
La variable pivotal es : =
~ ˆ(S, ) y por distribuirse Normal presenta simetría.
É*2
7
Ét
É
2 Ê −:
2 ÅÉ − :
*¥
*¥
7
Ét
É
<
É*2
7
Ét
É
< :
*¥ Ë
< Ì < É +:
ESTADÍSTICA
*¥
=
−¥
7 Æ=
Ét
É
−¥
DAEZEGO
Intervalo para dos poblaciones
Intervalo para Diferencia de Medias
Consideremos dos poblaciones normales N μ> , σ>Ÿ ) y N(μŸ , σŸŸ )
El parámetro a estimar es 6 − 6 y entonces el estimador es
-
−
Con varianzas poblacionales Í y Í conocidas
La variable pivotal es : =
(
*
Ð
2 Ï−:
2 Ô(
)−:
−
Î
*¥
7
Í
¦
*¥
+
)*(6 *6 )
Í
Í
~ˆ(S, )
<
(
Í
<6 −6 <(
*
)*(6 *6 )
Í
¦
Í
<:
Ó
*¥ Ò
Ñ
=
)+:
−
−¥
*¥
7
Í
+
Í
Õ=
−¥
Este intervalo también se puede usar en el caso de que las poblaciones no sean normales y
las varianzas poblacionales sean desconocidas, siempre que el tamaño de las muestras sea
mayor a 30. Lo único que hacemos es usar las varianzas muestrales en lugar de las
poblacionales.
-
Las varianzas poblacionales °>Ÿ y °ŸŸ son desconocidas y supuestas iguales
La variable pivotal es
2 Ô(
−
)−
=
*¥
(
8' 7
*
)*(6 *6 )
8' 7
+
~
(
* )
<6 −6 <(
; 8' = 7
)+
−
(
* )8
(
*¥
(
8' 7
Intervalo de Confianza para Cociente de Varianzas
* )8
* )
+
Õ=
−¥
Tenemos dos poblaciones normales N(μ> , σ>Ÿ ) y N(μŸ , σŸŸ ). El estadístico que estima a
5 ⁄5 es 8 ⁄8 . Entonces la variable pivotal es: + = 8
8 5
ESTADÍSTICA
5
~ +(
* ,
* )
DAEZEGO
Prueba de Hipótesis
Hipótesis estadística: es una afirmación de un conjunto de parámetros de la distribución
poblacional. La aceptación de una hipótesis implica tan sólo que los datos no proporcionan
evidencia suficiente para refutarla. Por otro lado, el rechazo implica que la evidencia de la
muestra la refuta.
-
-
Hipótesis Nula (H0): es la afirmación respecto de algún parámetro que ya se conocía
por experiencias previas. Indica una situación que ocurre normalmente. En esta
hipótesis aparece siempre el signo igual.
Hipótesis Alternativa (H1): es aquella que contradice a la hipótesis nula. Representa
una situación nueva.
A una hipótesis que, si es verdadera, especifica completamente a la distribución
poblacional se la llama hipótesis simple, y a una que no la especifica se la llama
hipótesis compuesta.
Dada una muestra aleatoria X1, X2,…, Xn de tamaño n, definimos la región crítica o de
rechazo C al conjunto de todos los valores del estadístico que hacen que la H0 sea
rechazada.
Entonces la prueba determinada por la región critica o de rechazo C es:
-
No rechazar H0 si w , w , … , w ) ∈ Ö
Rechazar H0 si (w , w , … , w ) ∈ Ö
Tenemos varias alternativas a la hora de tomar la decisión de rechazar o no la H0:
-
2('
2('
) = 2( '
) = 2( '
:
×S ! ! t
×S ! ! t
'
)=¥
)=‘
La regla de decisión es buena cuando el error de tipo 1 y 2 es pequeño. En general se
fija la probabilidad de cometer el error tipo1 y se trata de minimizar la probabilidad de
cometer el error tipo 2. Tener en cuenta que ¥ + ‘ ≠ . A α se la suele llamar nivel de
significancia.
ESTADÍSTICA
DAEZEGO
Pruebas relacionadas con la media poblacional con varianza conocida
Como conocemos la varianza poblacional, la variable fundamental o pivotal que
usaremos para hacer la prueba de hipótesis es la z ya que suponemos normalidad. Dada
una H0 planteamos una H1 como sigue:
ÙÚ : Ç ≥ Ü
Ù> : Ç < Ü
Donde k es el valor conocido de µ. Notar que sólo en H0 se coloca el signo igual, y que
la H1 refuta a la H0.
Ahora se precede a plantear la región crítica o de rechazo, para ello empleamos el
E.M.V. para µ:
α
Ý ! Ý: X < Þ| Ì X < Þ |àá
; |àá indica que el se usa el µ del ÙÚ
Notar que α siempre esta en la región de rechazo.
Ahora se procede a estandarizar y despejar el valor de C:
2Å
*6
5⁄√
Entonces si
Q6
5⁄√
2 Å: <
:¥
<
Q6
5⁄√
Q6
5⁄√
Æ |àá
Æ |àá
6 ) :¥ .
< Þ rechazamos la ÙÚ al nivel de significancia α.
Así podemos tener dos tipos de Test o Prueba:
-
¥
¥
5
√
Test Unilateral o de una cola: ×S : º ºS y × : º > ºS
Test Bilateral o de dos colas: ×S : º ºS y × : º ≠ ºS
× : º < ºS
Propiedades
- Los errores tipo 1 y 2 están relacionados entre sí. La disminución de probabilidad de
uno resulta en el aumento de la probabilidad del otro.
- Un incremente en el tamaño n de la muestra reduce simultáneamente los valores de
α y β.
- La probabilidad de cometer error de tipo 1 puede reducirse ajustando el o los
valores críticos de la región de rechazo.
ESTADÍSTICA
DAEZEGO
Tamaño de la muestra
Ahora veremos como determinar el tamaño n de una muestra teniendo H0 y H1 así como
los valores de α y β que nos queremos permitir.
Primero planteamos la región de rechazo de donde vamos a despejar el valor de C:
ÙÚ : ÇÚ
Ý ! Ý: X > Þ| Ì X > Þ |ãá
2 ": >
*6
5⁄ √
# |×S
¥
Ü
Ù> : Ç> > Ü
α
2 ": <
*6
5⁄√
# | ×S
Q¥
6S ) :
*¥
.
5
√
Ahora planteamos la región de aceptación (donde está β) y vamos a despejar el valor de
C:
Ý ! C: X < Þ| Ì X < Þ |ãž
2 ": <
*6
5⁄ √
# |×
β
‘
6 ) :‘ .
5
√
Sigue restar miembro a miembro las dos ecuaciones que encontramos y así podremos
hallar el valor de n:
S
6S ) :
*¥
.
5
√
Q "6 ) :‘ .
5
√
#
n: debemos tomar un valor entero
Pruebas relacionadas con la varianza poblacional
Aquí también supondremos normalidad, por ello y por tratarse de la varianza la variable
pivotal que usaremos será la χ2
Se procede de igual manera, planteando la región de rechazo y hallando el valor de C,
para luego evaluar si se acepta o rechaza la H0 al nivel de significancia con el que se
esta trabajando. En este caso el E.M.V de la varianza poblacional es S2.
ÙÚ : ° < Ü
Ù> : ° > Ü
Ý ! Ý: SŸ > Þ| Ì SŸ > Þ |ãá
2 "— >
*
5
# |×S
¥
α
2 "— <
*
5
# | ×S
ESTADÍSTICA
Q¥
*
5
—
*¥,( * )
DAEZEGO
Pruebas relacionadas con dos poblaciones normales
Vamos a analizar el caso de cociente de varianzas y el de diferencia de medias.
-
Cociente de varianzas
En este caso tenemos dos poblaciones normales N μ> , σ>Ÿ ) y N(μŸ , σŸŸ ) de las que se toman
dos muestras aleatorias independientes de tamaño n1 y n2 respectivamente. Por lo tanto la
variable pivotal a emplear en este caso es la F, dado que estamos trabajando con cociente
de varianzas.
Las hipótesis a plantear son:
ÙÚ : °>Ÿ ⁄°ŸŸ = 1
Ù> : °>Ÿ ⁄°ŸŸ ≠ 1
Ý ! Ý: S>Ÿ ⁄SŸŸ < C> o S>Ÿ ⁄SŸŸ > CŸ | P(S>Ÿ ⁄SŸŸ < C> )|ãá + P(S>Ÿ ⁄SŸŸ > CŸ )|ãá = α
P(S>Ÿ ⁄SŸŸ < C> )|ãá =
P(F < C> )|ãá =
ç
Ÿ
ç
Ÿ
; P(S>Ÿ ⁄SŸŸ > CŸ )|ãá =
; P(F > CŸ )|ãá =
C> = Fç (n> − 1, nŸ − 1) =
Ÿ
CŸ = F>*ç (n> − 1, nŸ − 1)
Ÿ
ç
Ÿ
1
F>*ç (nŸ − 1, n> − 1)
ç
Ÿ
P(F < CŸ )|ãá = 1 −
ç
Ÿ
Ÿ
No rechazamos la H0 si el 1 cae dentro de la región de aceptación.
Rechazamos la H0 si no ocurre lo anterior.
-
Diferencia de Medias
En este caso tenemos dos poblaciones normales N(μ> , σ>Ÿ ) y N(μŸ , σŸŸ ) de las que se toman
dos muestras aleatorias independientes de tamaño n1 y n2 respectivamente. Supondremos
que las varianzas poblacionales son desconocidas pero que son iguales, entonces la variable
pivotal es una t.
ÙÚ : Ç> − ÇŸ = 0
Ù> : Ç> − ÇŸ < 0
Ý ! Ý: X> − X Ÿ < Þ| Ì(X> − X Ÿ < Þ )|ãá = α
ESTADÍSTICA
DAEZEGO
P Ôt <
ê
ž ž
ëì 7
íž í
Õ |ãá
α
C
Qt>*ç Sî 7ížž ) íž
No rechazamos la H0 si el cero cae en la región de aceptación.
Potencia de la Prueba o Test
Es una función que se define así:
ï θ>
1 − –(θ> ) ðñ θ> ≠ θ
v
ò
ðñ θ> = θ
Lo primero que hacemos es plantear la región de rechazo y encontrar el valor de C que
corresponda. Luego procedemos a encontrar el valor de β planteando la región de
aceptación, tomando el valor de C calculado anteriormente y usando también el valor dado
de θ> . Una vez obtenido el valor de β procedemos a usar la ecuación para calcular la
potencia del test.
ESTADÍSTICA
DAEZEGO
Regresión y Correlación Lineal
La regresión lineal es una herramienta que estudia la dependencia existente entre una
variable dependiente, llamada variable respuesta, y una o más variables independientes
llamadas variables predictores. Nosotros veremos el caso de la regresión lineal simple así
que trabajaremos con una variable predictor y una variable respuesta. Es decir que el
análisis de regresión consiste en encontrar una relación que ligue los predictores con
la respuesta.
Un primer método para saber si existe relación entre las variables es emplear un
dispersograma que no es mas que un sistema coordenado en el cual graficamos los pares de
valores xó , yó ) con i |>µ
Ahora veremos un método para elegir la recta de regresión que se llama método de
mínimos cuadrados.
Este método implica la suma de los cuadrados de las distancias verticales de los puntos yi a
la recta sea lo mas pequeña posible.
La recta poblacional será ] = ¥ + ‘
y la recta muestral l =
+K
Planteamos la ecuación de distancia D y luego debemos encontrar los valores de a y b de
manera tal que D sea mínima:
0( , K) = XVl − ( + K )W
Para que D sea mínima debemos encontrar sus derivadas parciales y luego las igualaremos
a cero para encontrar los valores de a y b respectivamente. De todo el trabajo algebraico se
obtiene que:
= X −K X
K=
∑ (
l
=]−K
8
− )(l − ])
=
∑ ( − )
8
Así hemos obtenido los coeficientes a y b de la recta l =
regresión de Y sobre X o recta de regresión muestral.
ESTADÍSTICA
l
+ K que se denomina
DAEZEGO
Para poder inferir sobre ]
siguientes supuestos:
-
¥) ‘
a partir de l
) K debemos considerar los
La variable X es una variable matemática, es decir no esta sujeta a errores.
La variable Y es una variable aleatoria que si está sujeta a errores.
Las variables Y1, Y2,…, Yn se consideran variables aleatorias independientes.
Para cada xi, tenemos que ] ~ˆ(¥ + ‘ , 5 ).
La varianza σ2 es constante.
Estimadores para α, β y α+βx
Pendiente de la recta de regresión muestral: b
K=
8 l
8
depende linealmente de las variables yi que se distribuyen normalmente, por lo
tanto b también se distribuye normal. Ahora veamos como se distribuye, tener en cuenta
que sólo colocamos los resultados pasando por alto los desarrollos algebraicos.
EVbW = β y VVbW =
´
∑í
ž (ö÷ *a)
Podemos realizar la siguiente estandarización:
K− ‘
:= 5
~ ˆ(S, )
{
^∑ ( − )
Con esta variable podemos construir intervalos de confianza y pruebas de hipótesis para la
pendiente β de la recta de regresión conociendo la varianza.
Ordenada al origen de la recta de regresión muestral: a
Recordemos que = ] − K , entonces por ser la combinación lineal de variables
aleatorias normales, a también se distribuye normal. Veamos sus parámetros:
EVaW = α y VVaW = σŸ ¡ + ∑í
>
µ
Podemos realizar la siguiente estandarización:
:=
5¦ +
− ¥
∑ (
− )
ESTADÍSTICA
a
ž (ö÷ *a)
~ ˆ(S, )
¢
DAEZEGO
Recta de regresión muestral: a+bx
De la misma forma que hicimos con a y b, podemos trabajar para encontrar los parámetros
de la a+bx. Se demuestra que ù ) Pú òû
) –ú y además para un valor dado de x: x0
ü Vù ) PúÚ W
ò ) –úÚ y VVù ) PúÚ W
σŸ ¡µ ) ∑í áö
>
ö *a
ž
á *a
¢
Podemos realizar la estandarización:
:
‡ ) ýrS Q þ ) rS
5¦ )
∑
S
Q
SQ
~ ˆ(S, )
Supongamos que queremos estimar ] = ¥ + ‘ , estaríamos estimando una variable
aleatoria: el valor de y0 para un valor x0 dado. Podemos llamar
εó = Yó − (α + βXó )
Donde εó es una variable aleatoria con EVεó W = 0 y VVεó W = σŸ . Su estimador puntual será
entonces eó = Yó − (a + bXó ), su esperanza es:
EVeó W = 0 = EVYó W − EVα + βX ó W
1
(xÚ − X)Ÿ
k
VVeó W = VVYó W + VVα + βXó W = σŸ + σŸ j + µ
n ∑> (xÚ − X)Ÿ
Dicho estimador depende linealmente de Yi. Realizamos la estandarización:
:=
] −( +K
5¦ +
+
S)
( S− )
∑ ( S− )
~ ˆ(S, )
Esta variable nos permite hallar los límites de confianza para el valor Y verdadero llamados
límites de predicción. Dichos límites comparados con los obtenidos para ù + PúÚ son más
amplios debido a las fluctuaciones por ser una variable aleatoria. Graficando los límites en
función de x0 tenemos que:
a y b son los límites para ò + –úÚ
c y d son los límites para Y0
LS límite superior
LI límite inferior
ESTADÍSTICA
DAEZEGO
Estimación de la Varianza
En general se da el caso en que no conocemos la varianza σ2 por lo que debemos estimarla.
Entonces se estima mediante la varianza de los errores eó , es decir:
°Ÿ = ¯Ÿ =
∑=>Vœ − (ù + PO )WŸ
”−2
Se demuestra que EV¯ Ÿ W = σŸ entonces ¯ Ÿ es un estimador insesgado de σŸ . Luego
podemos emplear la variable
cuando desconocemos σŸ
(=*Ÿ)¨
Ÿ
~•(=*Ÿ)
para calcular las variables adecuadas para
´
La fórmula práctica para calcular ¯ Ÿ es: 8 = ∑ V] − ( + K )W =
SŸ =
Donde
µ*>
=
∑í
ž( ÷* )
µ*>
y SaŸ =
µ*>
=
∑í
ž (a÷ *a)
*
*
f8] − K 8 g
µ*>
Intervalos de Confianza
-
Para α con σ2 desconocida
Como no conocemos la varianza, y por los conocimientos ya adquiridos, la variable pivotal
para el intervalo es una t. Recientemente vimos también que
:=
*¥
5¦
∑ ( • )
~ ˆ(S, ) y que
( * )
5
~
( * )
Entonces podemos construir la variable pivotal como ya sabemos:
=
ˆ(S, )
7—(9) ⁄9
=
5¦
•¥
∑ ( • )
( • )
¦
( • )5
=
8 ¦
*¥
∑ ( • )
~
( * )
Dada una confianza y recordando que t tiene una distribución simétrica, podemos plantear
el intervalo:
2 "−
*¥
<›<
*¥ #
=
−¥
Luego hacemos los reemplazos y despejes que corresponden para obtener el intervalo de α.
ESTADÍSTICA
DAEZEGO
-
Para β con σ2 desconocida
Procediendo de igual manera y recordando que : =
5
K* ‘
7∑ ( * )
~ ˆ(S, )
Vamos a emplear nuevamente la variable pivotal t y a realizar los mismos pasos para
obtener el intervalo para β para un nivel de significancia dado.
-
Para la recta ] = ¥ + ‘ dado un valor x0
Nuevamente emplearemos una variable pivotal t porque no conocemos la varianza
poblacional y recordemos que : =
‡ ýrS * (þ
5¦
rS )
e S• h
∑ ( S• )
~ ˆ(S, ).
Dado un nivel de confianza procedemos a construir el intervalo de manera similar a como
venimos haciendo en los casos anteriores.
-
Para la ordenada Y (límite de predicción) dado un valor x0
Todo lo mismo, la variable pivotal sigue siendo una t y : =
5¦
] *(
K S)
e S• h
∑ ( S• )
~ ˆ(S, )
Procedemos a construir la variable t y para un nivel de significancia dado construimos el
intervalo para Y.
Prueba de Hipótesis
Debemos probar si algún parámetro es igual a algún valor hipotético.
-
Prueba para β
ÙÚ : – = –Ú
Ù> : – ≠ –Ú
La variable pivotal es la “bendita t”:
con la siguiente región de rechazo:
=
K* ‘
8 {7∑ ( * )
|K − ‘S | >
( *¥)
ESTADÍSTICA
~
( * )
8
7∑ ( * )
DAEZEGO
-
Prueba para α
ÙÚ : ò = òÚ
Ù> : ò ≠ òÚ
=
La variable pivotal es la “bendita t”:
8 ¦
*¥
∑ ( • )
| − ¥S | >
con la siguiente región de rechazo:
~
e *¥h 8
( * )
7 +∑
( * )
Regresión Curvilínea
-
Función Polinómica
De manera general tenemos que ] = ¥ + ‘ + ’
»=
la cual debemos ajustar a l = ]
-
S
Función Potencial
Debemos ajustar una curva ] = ¥
+
+
+
+
»=
a l=]
‘
¼
¼
+ ⋯+š
¼
+⋯+
K
Aplicando logaritmo natural para valores positivos de a y b tendremos:
l
)K
]
; haciendo las sustituciones
C)K
Vemos que tenemos una función lineal, por lo que podemos aplicar la regresión lineal
teniendo en cuenta que la tabla de datos va a ser
con
l .
]
]
]
-
Otras funciones
¥)
¥ ‘
¥ ‘
‘
]
]
]
¥)‘
¥)‘
¥)‘
donde
donde ]
donde ]
l
l
ESTADÍSTICA
DAEZEGO
Correlación Simple
Al realizar una predicción del valor de Y usando la ecuación de mínimos cuadrados, la
misma está sujeta a errores. El grado de exactitud en la predicción depende de la
correlación que existe entre las dos variables. La medida usual es el coeficiente de
correlación ρ (si es poblacional) o r (si es muestral).
Entonces como es de esperar si r es pequeño se obtiene poca precisión al realizar
predicciones sobre el valor de Y usando la recta de mínimos cuadrados. Por otro lado si r es
aproximadamente 1 o -1 la correlación es fuerte lo que se traduce en que la recta de
mínimos cuadrados es cercana a todos los puntos del dispersograma y se logran gran
exactitud al efectuar la predicción.
En base a r se estima si ρ si tiene un determinado valor, esto es porque r es un E.M.V de ρ.
Recordemos que:
ρ=
î
( a, )
´ ´
=
=
Su estimador se define como:
∑í
ž e ÷ • he ÷ • h
í
í
¦ ∑ž e ÷ • h
í
8 l
^8 8ll
í
¦∑ž e ÷ • h
í
− ≤
=
−1 ≤ ρ ≤ 1
^
≤
Cuando r = -1 o r = 1, significa que existe un ajuste perfecto. Por otro lado cuando r = 0
significa que no existe correlación lineal (podría ser una relación curvilínea).
La diferencia entre el análisis de regresión y el de correlación es que en este último
tanto X como Y son variables aleatorias.
Una hipótesis útil es ρ = 0 es decir que no hay relación entre X e Y porque serían
independientes. Entonces: ×S : = S
× :
≠S
ρ = 0 se usa sólo para test de hipótesis y no para intervalos de confianza
La relación de r que usamos es: r = b7
K
=
√ −
√ −
=
; b=
^ −
y se demuestra que
⁄ −
~
( * )
Con esta variable se hace la prueba con la siguiente región de rechazo dado un nivel de
| K | > *¥,( * )
significancia α:
ESTADÍSTICA
DAEZEGO
Otra hipótesis es si la muestra proviene de una población con ρ0, es decir
×S :
Partiendo de que:
e
„
•„
z
h ~•"
× :
"
S
• S
=
≠
#,
S
S
*¼
# entonces resulta
1
1 >
lne>* h − 2 ln ">>* SS #
2
=
~N(0,1)
1
7
n−3
Y empleamos la siguiente región de rechazo para probar H0
|z | > ¶>*
ESTADÍSTICA
Anuncio
Documentos relacionados
Descargar
Anuncio
Añadir este documento a la recogida (s)
Puede agregar este documento a su colección de estudio (s)
Iniciar sesión Disponible sólo para usuarios autorizadosAñadir a este documento guardado
Puede agregar este documento a su lista guardada
Iniciar sesión Disponible sólo para usuarios autorizados