taller #1 - Estabilidad de taludes

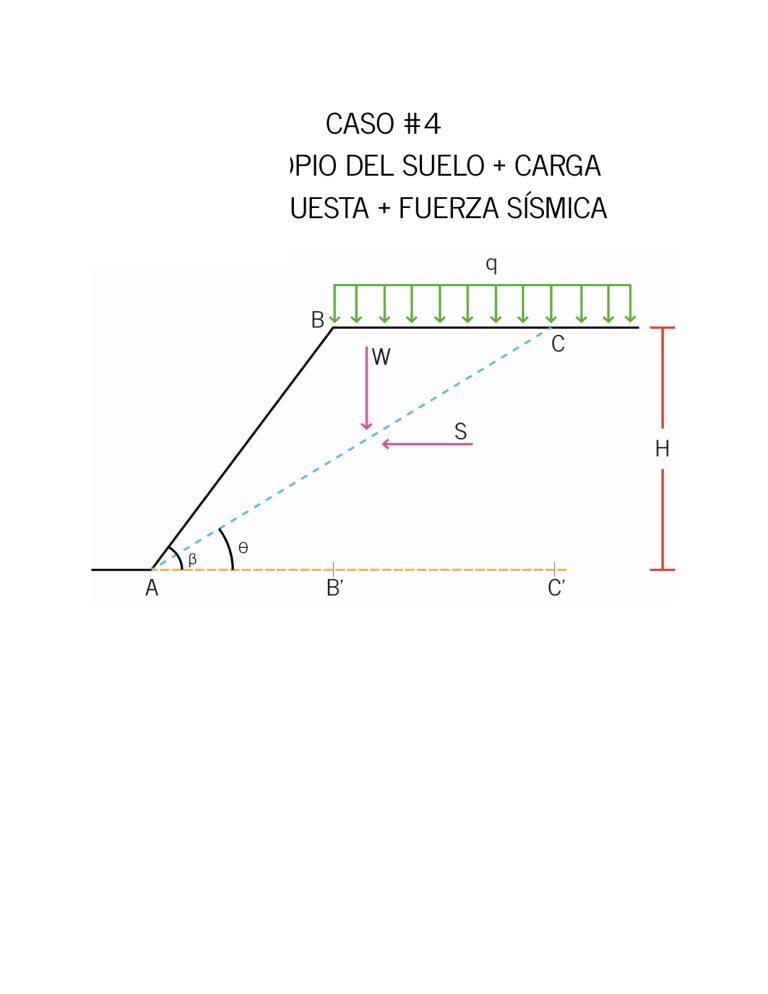
CASO #4
PESO PROPIO DEL SUELO + CARGA
SOBREIMPUESTA + FUERZA SÍSMICA
Área cuña
Área cuña
((b ⋅ h))
Ac ＝ ――
2
BC ⋅ H
Ac ＝ ―――
2
AC'
cot ((θ)) ＝ ――
H
AB'
cot ((β)) ＝ ――
H
BC ＝ AC' - AB'
AC' ＝ H ⋅ cot ((θ))
AB' ＝ H ⋅ cot ((β))
BC ＝ ((H ⋅ cot ((θ)))) - ((H ⋅ cot ((β))))
Ahora
((H ⋅ cos ((θ)))) ((H ⋅ cos ((β))))
((H ⋅ cot ((θ)))) - ((H ⋅ cot ((β)))) ＝ ――――
- ――――
sin ((θ))
sin ((β))
((H ⋅ cos ((θ)) ⋅ sin ((β)))) - ((H ⋅ cos ((β)) ⋅ sin ((θ))))
―――――――――――――
sin ((θ)) ⋅ sin ((β))
H ⋅ ((((cos ((θ)) ⋅ sin ((β)))) - ((cos ((β)) ⋅ sin ((θ))))))
―――――――――――――
sin ((θ)) ⋅ sin ((β))
H ⋅ sin ((β - θ))
((H ⋅ cot ((θ)))) - ((H ⋅ cot ((β)))) ＝ ―――――
sin ((θ)) ⋅ sin ((β))
Reemplazando el valor de BC en la ecuación inicial del área de la cuña
2
H
sin ((β - θ))
⋅ ―――――⎛⎝m 2 ⎞⎠
Ac ＝ ――
2 sin ((θ)) ⋅ sin ((β))
H H ⋅ sin ((β - θ))
Ac ＝ ―⋅ ―――――
2 sin ((θ)) ⋅ sin ((β))
Peso de la cuña
2
Wc ＝ A c ⋅ γ ⋅ 1 m
H
sin ((β - θ))
⋅ ―――――
⋅γ
Wc ＝ ――
2 sin ((θ)) ⋅ sin ((β))
2
H
sin ((β - θ))
⋅ γ ⋅ ―――――
Wc ＝ ――
sin ((θ)) ⋅ sin ((β))
2
Se aplica la descomposición vectorial al peso de la cuña, con respecto a la sección AC
Componente de carga
Wcy
cos ((θ)) ＝ ――
Wc
Wcx
sin ((θ)) ＝ ――
Wc
Wcy ＝ Wc ⋅ cos ((θ))
Wcx ＝ Wc ⋅ sin ((θ))
WN ＝ Wcy
H2
sin ((β - θ))
⋅ γ ⋅ ―――――
⋅ cos ((θ))
WN ＝ ――
2
sin ((θ)) ⋅ sin ((β))
Wτ ＝ Wcx
H2
sin ((β - θ))
⋅ γ ⋅ ―――――
⋅ sin ((θ))
Wτ ＝ ――
2
sin ((θ)) ⋅ sin ((β))
Componente de carga
qp ＝ qd ⋅ BC ⋅ 1 m
H ⋅ sin ((β - θ))
qp ＝ qd ⋅ ――――― ((kN))
sin ((θ)) ⋅ sin ((β))
Se procede a descomponer la carga
qpy
cos ((θ)) ＝ ――
qp
qpx
sin ((θ)) ＝ ――
qp
qpy ＝ qp ⋅ cos ((θ))
qpx ＝ qp ⋅ sin ((θ))
qN ＝ qpy
qτ ＝ qpx
sin ((β - θ))
⋅ cos ((θ))
qN ＝ qd ⋅ ―――――
sin ((θ)) ⋅ sin ((β))
sin ((β - θ))
⋅ sin ((θ))
qτ ＝ qd ⋅ ―――――
sin ((θ)) ⋅ sin ((β))
Componente de sismo
Svy
cos ((θ)) ＝ ――
Sv
Svx
sin ((θ)) ＝ ――
Sv
Svy ＝ Sv ⋅ cos ((θ))
Svx ＝ Sv ⋅ sin ((θ))
Shy
cos ((θ)) ＝ ――
Sh
Shx
sin ((θ)) ＝ ――
Sh
Shy ＝ Sh ⋅ cos ((θ))
Shx ＝ Sh ⋅ sin ((θ))
Se tiene lo siguiente
Sv ＝ Kv ⋅ Wc
Sh ＝ Kh ⋅ Wc
Sismo en dir. vertical
Sismo en dir. horizontal
En dirección Vertical
Svy ＝ ⎛⎝Kv ⋅ Wc⎞⎠ ⋅ cos ((θ))
En dirección Horizontal
Shy ＝ ⎛⎝Kh ⋅ Wc⎞⎠ ⋅ cos ((θ))
Svx ＝ ⎛⎝Kv ⋅ Wc⎞⎠ ⋅ sin ((θ))
Shx ＝ ⎛⎝Kh ⋅ Wc⎞⎠ ⋅ sin ((θ))
FUERZAS NORMALES (en dirección Y)
Svx ＝ ⎛⎝Kv ⋅ Wc⎞⎠ ⋅ sin ((θ))
Shx ＝ ⎛⎝Kh ⋅ Wc⎞⎠ ⋅ sin ((θ))
FUERZAS NORMALES (en dirección Y)
ΣFy
Wcy + qpy + Svy - Shy
⎛⎝Wc ⋅ cos ((θ))⎞⎠ + ⎛⎝qp ⋅ cos ((θ))⎞⎠ + ⎛⎝Sv ⋅ cos ((θ))⎞⎠ - ⎛⎝Sh ⋅ sin ((θ))⎞⎠
⎛⎝cos ((θ)) ⋅ ⎛⎝Wc + qp + Sv⎞⎠⎞⎠ - ⎛⎝Sh ⋅ sin ((θ))⎞⎠
FUERZAS CORTANTES (en dirección X)
ΣFy
Wcx + qpx + Svx - Shx
⎛⎝Wc ⋅ sin ((θ))⎞⎠ + ⎛⎝qp ⋅ sin ((θ))⎞⎠ + ⎛⎝Sv ⋅ sin ((θ))⎞⎠ - ⎛⎝Sh ⋅ cos ((θ))⎞⎠
⎛⎝sin ((θ)) ⋅ ⎛⎝Wc + qp + Sv⎞⎠⎞⎠ - ⎛⎝Sh ⋅ cos ((θ))⎞⎠
ESFUERZO NORMAL ( σN )
FN
σN ＝ ――
AC
FN
σN ＝ ―――
H
―――
sin ((θ))
FN ⋅ sin ((θ))
σN ＝ ――――
H
⎛⎝⎛⎝cos ((θ)) ⋅ ⎛⎝Wc + qp + Sv⎞⎠⎞⎠ - ⎛⎝Sh ⋅ sin ((θ))⎞⎠⎞⎠ ⋅ sin ((θ))
σN ＝ ―――――――――――――――
H
ESFUERZO CORTANTE ( στ )
Fτ
στ ＝ ――
AC
Fτ
στ ＝ ―――
H
―――
sin ((θ))
Fτ ⋅ cos ((θ))
στ ＝ ――――
H
⎛⎝⎛⎝sin ((θ)) ⋅ ⎛⎝Wc + qp + Sv⎞⎠⎞⎠ - ⎛⎝Sh ⋅ cos ((θ))⎞⎠⎞⎠ ⋅ sin ((θ))
στ ＝ ―――――――――――――――
H
FACTOR DE SEGURIDAD( FSS )
SF
FSS ＝ ―
τd
σN + c' ⋅ tan ((ϕ'))
FSS ＝ ―――――
στ
⎛ ⎛⎝⎛⎝cos ((θ)) ⋅ ⎛⎝Wc + qp + Sv⎞⎠⎞⎠ - ⎛⎝Sh ⋅ sin ((θ))⎞⎠⎞⎠ ⋅ sin ((θ)) ⎞
⎜―――――――――――――――
⎟ + c' ⋅ tan ((ϕ'))
H
⎝
⎠
FSS ＝ ―――――――――――――――――――
⎛⎝⎛⎝sin ((θ)) ⋅ ⎛⎝Wc + qp + Sv⎞⎠⎞⎠ + ⎛⎝Sh ⋅ cos ((θ))⎞⎠⎞⎠ ⋅ sin ((θ))
―――――――――――――――
H
ANÁLISIS DE RESULTADOS
La finalidad del software GEO5 es calcular el valor mínimo del factor de seguridad para
el talud en análisis. Adicional al resultado anterior, también nos suministra la sección
de falla mas crítica.
Este análisis se llevó a cabo por los métodos de Bishop y Spencer, implementando un
método de optimización. Se analizaron taludes con ángulos comprendidos entre los 60°
y 80°, obteniéndose los siguientes resultados.
Ángulo Beta
60
65
70
75
80
Método Bishop
1.24
1.16
1.09
1.01
0.94
Método Spencer
1.31
1.42
1.43
1.45
1.47
De la anterior tabla es posible observar 2 tendencias:
-
Por el método Bishop se observa que los valores de FS se alejan del valor mínimo
para que el talud pueda ser considerado como estable.
-
Por el método Spencer estos mismos valores se acercan al valor mínimo
aceptable para la estabilidad del talud.
CONCLUSIONES
Para el cálculo de los factores de seguridad de los taludes, con los distintos ángulos de
inclinación suministrados se empleó la herramienta GEO5, tomando como base los
métodos de Bishop y Spencer, ambos por optimización, y, adicional a esto, se utilizó la
herramienta “Microsoft Excel” para el cálculo por el método de cullman, teniendo en
cuenta la demostración del caso asignado de estabilidad de taludes.
Si bien es importante conocer el manejo de este software, es fundamental poder
desarrollar un manejo sólido de Excel, ya que la función central del software es verificar
lo previamente calculado.
La importancia de esta herramienta tecnológica radica en el hecho de conocer, de forma
aproximada por medio de una simulación, el comportamiento del talud en condiciones
reales, lo que nos permite asimilar de una forma más eficiente y objetiva los
conocimientos teóricos impartidos acerca del tema.
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Bishop)
Sum of active forces :
Fa = 296,95 kN/m
Sum of passive forces : Fp = 368,37 kN/m
Sliding moment :
Ma = 4620,55 kNm/m
Resisting moment :
Mp = 5731,79 kNm/m
Factor of safety = 1,24 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Spencer)
Factor of safety = 1,31 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Bishop)
Sum of active forces :
Fa = 289,79 kN/m
Sum of passive forces : Fp = 336,43 kN/m
Sliding moment :
Ma = 4685,88 kNm/m
Resisting moment :
Mp = 5440,04 kNm/m
Factor of safety = 1,16 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Spencer)
Factor of safety = 1,42 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Bishop)
Sum of active forces :
Fa = 290,48 kN/m
Sum of passive forces : Fp = 315,46 kN/m
Sliding moment :
Ma = 5237,29 kNm/m
Resisting moment :
Mp = 5687,75 kNm/m
Factor of safety = 1,09 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Spencer)
Factor of safety = 1,43 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Bishop)
Sum of active forces :
Fa = 280,98 kN/m
Sum of passive forces : Fp = 284,10 kN/m
Sliding moment :
Ma = 5644,91 kNm/m
Resisting moment :
Mp = 5707,50 kNm/m
Factor of safety = 1,01 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Spencer)
Factor of safety = 1,45 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Bishop)
Sum of active forces :
Fa = 277,55 kN/m
Sum of passive forces : Fp = 259,57 kN/m
Sliding moment :
Ma = 6572,40 kNm/m
Resisting moment :
Mp = 6146,63 kNm/m
Factor of safety = 0,94 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]
Name :
Stage - analysis : 2 - 1
The slip surface after optimization.
Slope stability verification (Spencer)
Factor of safety = 1,47 < 1,50
Slope stability NOT ACCEPTABLE
[GEO5 - Slope Stability (demoversion) | version 5.2020.34.0 | Copyright © 2020 Fine spol. s r.o. All Rights Reserved | www.finesoftware.eu]