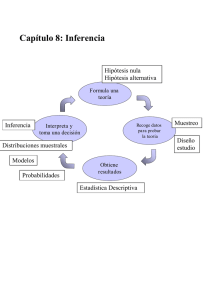
NATURALEZA DE LA PRUEBA DE HIPÓTESIS Todo mundo toma decisiones en la vida diaria. Algunas de estas decisiones son de fundamental importancia y otras son aparentemente insignificantes. Todas las decisiones siguen el mismo patrón básico. Se ponderan las alternativas; luego, con base en las convicciones y preferencias personales, y cuáles sean los hechos disponibles, se llega a una decisión y se emprende la acción idónea. La prueba de hipótesis sigue casi el mismo proceso, excepto que implica información estadística. El proceso de toma de decisiones comienza con la identificación de algo de interés y luego con el planteamiento de dos hipótesis al respecto. HIPÓTESIS Afirmación de que algo es verdadero. PRUEBA DE HIPÓTESIS ESTADÍSTICA Proceso que permite tomar una decisión entre dos hipótesis opuestas. Estas hipótesis se plantean de modo que una es la negación de la otra (de esta forma una de ella siempre es verdadera y la otra siempre es falsa). Luego, una hipótesis se prueba con la esperanza de poder demostrar que su ocurrencia es muy improbable, implicándose así que la otra hipótesis es probablemente la verdadera. Las dos hipótesis presentes en la toma de una decisión se denomina hipótesis nula e hipótesis alternativa. HIPÓTESIS NULA, H0 Es la hipótesis que se prueba. Por lo general, es una afirmación sobre un parámetro poblacional que tiene un valor específico. La hipótesis nula se denomina así porque es el “punto inicial” de la investigación (en su interpretación a menudo se usa la frase “no hay diferencia”). HIPÓTESIS NULA, 𝑯𝒂 Es la afirmación sobre el mismo parámetro de la población que se usa en la hipótesis nula. En general, es una afirmación que especifica que el parámetro de la población tiene un valor diferente, de alguna manera, del valor proporcionado en la hipótesis nula. El rechazo de la hipótesis nula implica la probable veracidad de la hipótesis alternativa. Un paso muy importante es determinar las afirmaciones de las hipótesis nula y alternativa. La idea básica de la prueba de hipótesis es que los hechos tengan la posibilidad de “refutar” la 𝐻0 . La hipótesis nula es la afirmación que podría ser refutada por los hechos. Su interés (convicción o resultado deseado), como la persona que realiza la prueba, se expresa en la hipótesis alternativa. Siendo usted quien toma la decisión, considera que los hechos demostrarán la factibilidad de su “teoría” al demostrar la improbabilidad de la veracidad de la hipótesis nula. Algunas veces, la hipótesis alternativa se denomina hipótesis de investigación, ya que representa lo que el investigador espera encontrar como “verdadero” (de ser así, el investigador publicará un artículo sobre la investigación). Ejemplo 1 Se está probando un nuevo diseño de bolsas de aire, usadas en los automóviles, y se tiene interés en cuanto a que quizá no se abran de manera adecuada. Escriba la hipótesis nula y alternativa. Solución: Las dos posibilidades opuestas son: “las bolsas se abren correctamente” o “las bolsas no se abren correctamente”. La prueba sólo puede producir hechos que desacrediten la hipótesis: “las bolsas se abren correctamente”. En consecuencia, la hipótesis nula es “se abren correctamente” y la hipótesis alternativa es “no se abren correctamente”. La hipótesis alternativa puede ser la afirmación que el investigador desea demostrar que es verdadera. Ejemplo 2 Usted sospecha que un detergente de marca es mejor que el otro que vende la tienda de la esquina y desea probar ambos productos porque preferiría comprar el detergente más barato, que es el que expende la tienda. Establezca las hipótesis nula y alternativa. Solución: Su sospecha, “el detergente de marca es mejor que el detergente que vende la tienda de la esquina” es la razón para realizar la prueba, por lo que se vuelve la hipótesis alternativa. 𝐻0 : "No hay diferencia en el desempeño de los detergentes." 𝐻𝑎 : "El detergente de marca es mejor que el detergente que vende la tienda de la esquina." Sin embargo, como consumidor, espera no rechazar la hipótesis nula por razones presupuestarias. Antes de volver al ejemplo de la fiesta, es necesario considerar los cuatro resultados posibles que pueden obtenerse por el hecho de que la hipótesis nula sea verdadera o falsa y que la decisión sea “rechazar 𝐻0 ” o “no rechazar 𝐻0 ”. Hipótesis nula Decisión Verdadera Falsa No rechazar 𝑯𝟎 Decisión correcta de tipo A Error de tipo II Rechazar 𝑯𝟎 Error de tipo I Decisión correcta de tipo B Evaluación de las técnicas de enseñanza Resumen: este estudio prueba el efecto de la realización de tareas y cuestionarios escolares sobre los puntajes del examen. La hipótesis para este estudio es que un maestro puede mejorar el desempeño de un alumno (puntajes obtenidos en el examen) a través de influir sobre la probabilidad percibida esfuerzo-recompensa del estudiante. Un instructor logra lo anterior al asignar tareas (técnicas de enseñanza) que forman parte de la calificación del estudiante y que son percibidas por éste como un medio para mejorar su calificación en el curso. El estudiante está motivado para incrementar su esfuerzo a fin de completar estas tareas, que también deben mejorar su entendimiento sobre el material presentado en el curso. El resultado final esperado es obtener mejores puntajes en el examen. La hipótesis nula para este estudio es: 𝐻0 : "Las técnicas de enseñanza no tienen un efecto significativo sobre los puntajes de examen de los estudiantes." Una decisión correcta de tipo A ocurre cuando la hipótesis nula es verdadera y se decide a su favor. Una decisión correcta de tipo B ocurre cuando la hipótesis nula es falsa y la decisión es en oposición a la hipótesis nula. Un error de tipo I se comete cuando se rechaza una hipótesis nula verdadera; es decir, cuando la hipótesis nula es verdadera, pero se decide en contra de ella. Un error de tipo II se comete cuando se decide en favor de una hipótesis nula que realmente es falsa. Ejemplo 3 Describa los cuatro resultados posibles y las acciones resultantes que ocurrirían para la prueba de hipótesis del ejemplo 3. Solución: Recuerde 𝐻0 : “No hay diferencia en el desempeño de los detergentes.” 𝐻𝑎 : "El detergente de marca es mejor que el detergente que vende la tienda de la esquina." No rechazar 𝑯𝟎 Rechazar 𝑯𝟎 La hipótesis nula es verdadera La hipótesis nula es falsa Decisión correcta de tipo A Veracidad de la situación: no hay diferencia entre los detergentes. Conclusión: se determinó que no hay diferencia. Acción: el consumidor compra el detergente más barato, ahorra dinero y obtiene los mismos resultados. Error de tipo I Veracidad de la situación: no hay diferencia entre los detergentes. Conclusión: se determinó que el detergente de marca es mejor. Acción: el consumidor compra el detergente de marca, gasta dinero extra sin obtener mejores resultados. Error de tipo II Veracidad de la situación: el detergente de marca es mejor. Conclusión: se determinó que no hay diferencia. Acción: el consumidor compra el detergente más barato, ahorra dinero, pero obtiene peores resultados. Decisión correcta de tipo B Veracidad de la situación: el detergente de marca es mejor. Conclusión: se determinó que el detergente de marca es mejor. Acción: el consumidor compra el detergente de marca, gasta más y obtiene mejores resultados. NOTA: El error de tipo II a menudo resulta ser una “oportunidad pérdida”; pérdida en esta situación es la posibilidad de usar un producto que produce mejores resultados. Cuando se toma una decisión, sería agradable escoger siempre la opción correcta. Sin embargo, esto no es posible en estadística, ya que la decisión se toma con base en la información muestral. Lo mejor que puede esperarse es controlar la probabilidad con que ocurre un error. La probabilidad asignada al error de tipo I se denomina 𝛼 (“alfa”). La probabilidad del error de tipo II se denomina 𝛽 (“beta”). Error en la decisión Se rechaza una 𝐻0 verdadera No rechaza una 𝐻0 falsa Tipo Probabilidad Decisión correcta Tipo Probabilidad I 𝛼 A 1−𝛼 II 𝛽 No se rechaza una 𝐻0 verdadera Se rechaza una 𝐻0 falsa B 1−𝛽 Para controlar estos errores, a cada uno se le asigna una pequeña probabilidad. Los valores de probabilidad de mayor uso para 𝛼 y 𝛽 son 0.01 y 0.05. La probabilidad asignada a cada error depende de la gravedad de éstos. Mientras más grave es un error, menos se desea que ocurra, y en consecuencia se le asigna una menor probabilidad. Alfa y Beta son probabilidades de errores, cada una bajo condiciones separadas, y no pueden combinarse. Así, no es posible determinar una sola probabilidad para tomar una decisión incorrecta. De manera semejante, las dos decisiones correctas son distintas y ajenas, y cada una tiene su propia probabilidad; 1 − 𝛼 es la probabilidad de tomar una decisión correcta cuando la hipótesis nula es verdadera, y 1 − 𝛽 es la probabilidad de tomar una decisión correcta cuando la hipótesis nula es falsa. A 1 − 𝛽 se le denomina potencia de la prueba estadística, ya que mide la capacidad de una prueba de hipótesis para rechazar una hipótesis nula falsa, lo que es una característica muy importante. Recuerde: Sin importar el resultado de una prueba de hipótesis, nunca se tiene la certeza de haber tomado una decisión correcta. Se considerarán los dos errores de decisión posibles que pudieron cometerse en el ejemplo 4 cuando se probaron los detergentes. La mayoría de las personas se molestaría al descubrir que están gastando dinero extra por un detergente cuyo desempeño no es mejor que el de la marca más barata. De manera semejante, la mayoría de las personas se molestaría al describir que hubieran podido comprar un mejor detergente. La evaluación de la gravedad relativa de estos errores requiere saber, se trate de una persona que lave su ropa o de una empresa profesional de lavandería, qué tanto más cuesta el detergente de marca, etc. NIVEL DE SIGNIFICANCIA 𝜶 Es la probabilidad de cometer el error de tipo I. Establecer el nivel de significancia puede interpretarse como una “decisión gerencial”. Por lo general, alguien a cargo determina el nivel de probabilidad con que se desea arriesgar un error de tipo I. En este momento del procedimiento de prueba de hipótesis se recolectan y resumen los hechos y se calcula el valor de una estadística de prueba. ESTADÍSTICA DE PRUEBA Es la variable aleatoria cuyo valor se calcula a partir de los datos muestrales y que se utiliza para tomar la decisión de “no rechazar 𝐻0 ” o “rechazar 𝐻0 ”. El valor de la estadística de prueba calculado se usa junto con una regla de decisión para determinar si “rechaza 𝐻0 ” o “no se rechaza 𝐻0 ”. Esta regla de decisión debe establecerse antes de recolectar los datos y específica como se llegará a ella. Para completar una prueba de hipótesis, es necesario escribir una conclusión que describa cuidadosamente el significado de la decisión relativa al propósito de dicha prueba. LA CONCLUSIÓN a. Si la decisión es “rechazar 𝑯𝟎 ”, entonces la conclusión debe verbalizarse más o menos como “hay suficientes hechos al nivel de significancia 𝜶 para demostrar que… (el significado de la hipótesis alternativa)”. b. Si la decisión es “no rechazar 𝑯𝟎 ”, entonces la conclusión debe verbalizarse más o menos como “no hay suficientes hechos al nivel de significancia 𝜶 para demostrar que… (El significado de la hipótesis alternativa)”. Al escribir la decisión y la conclusión, recuerde que 1) la primera es sobre 𝐻0 y 2) la segunda es una afirmación acerca de la confirmación o no del argumento de 𝐻𝑎 . Esto es consistente con la “actitud” de todo el procedimiento de la prueba de hipótesis. La hipótesis nula es la afirmación que está “en juicio” y, por tanto, la decisión debe versar sobre ella. El argumento de la hipótesis alternativa es el pensamiento que ocasionó la necesidad de una decisión. En consecuencia, al escribir la conclusión debe contestarse la cuestión que condujo a la hipótesis alternativa. PRUEBA DE HIPÓTESIS DE LA MEDIA 𝝁 (𝝈 CONOCIDA): ENFOQUE DEL VALORPROBABILIDAD Supuesto para pruebas de hipótesis sobre la media 𝝁 usando una 𝝈 conocida: la distribución muestral de 𝑥̅ se comporta de manera normal. La distribución muestral de medias muestrales, 𝑥̅ , está distribuida alrededor de una media igual a 𝜇̅ con un error estándar de 𝜎/√𝑛, y se distribuye de manera normal cuando las muestras se eligen aleatoriamente de una población normal o cuando el tamaño de la muestra es suficientemente grande. La prueba de hipótesis es un procedimiento paso a paso bien organizado que se aplica para tomar una decisión. Para la prueba de hipótesis suelen usarse dos formatos diferentes. El enfoque que del valor-probabilidad, o simplemente el enfoque del valor-p, es el proceso de prueba de hipótesis que ha adquirido popularidad en años recientes, en gran medida como resultado de conveniencia y capacidad de “pulverización de números” de la computadora. Este método organizado como un procedimiento de cinco pasos. La prueba de hipótesis del valor-probabilidad: Procedimiento de cinco pasos Paso 1: Describir el parámetro de la población de interés. Paso2: Establecer la hipótesis nula (𝐻0 ) y la hipótesis alternativa (𝐻𝑎 ) Paso 3: Especificar los criterios de la prueba. a. Comprobar los supuestos. b. Identificar la estadística de prueba a utilizar. c. Determinar el nivel de significancia, 𝛼. Paso 4: Recolectar y presentar los hechos muestrales. a. Recolectar la información muestral. b. Calcular el valor de la estadística de prueba. c. Calcular el valor-p. Paso 5: Determinar los resultados. a. Determinar si el valor-p es menor o no que 𝛼. b. Tomar una decisión sobre 𝐻0 . c. Escribir una conclusión sobre 𝐻𝑎 . Un fabricante de aviones comerciales compra remaches para ensamblar las aeronaves. Cada proveedor de remaches que desea venderlos al fabricante de aviones, debe demostrar que sus productos cumplen con las especificaciones requeridas. Una de estas especificaciones es: “La resistencia media a la rotura de todos los remaches, 𝜇, debe ser por lo menos de 925 lb”- Cada vez que este fabricante compra remaches, está preocupado porque la resistencia media a la rotura pueda ser inferior a la especificación de 925 lb. NOTA 1: Cada remache tiene una resistencia a la rotura que es determinada al medir la fuerza necesaria para cortarlo. Resulta evidente la imposibilidad de probar todos los remaches. En consecuencia, se examinará una muestra de remaches y la decisión sobre la resistencia media de toda la población de interés estará basada en la meda de los productos muestreados y probados. NOTA 2: Para el ejemplo de los remaches se usará 𝜎 = 18. Paso 1: Describir el parámetro de la población de interés. El parámetro de la población de interés es la resistencia media, 𝜇, a la rotura (o fuerza para cortar) de los remaches en consideración para su compra. Paso 2: Establecer la hipótesis nula (𝐻0 ) y la hipótesis alternativa (𝐻𝑎 ). La hipótesis nula y la alternativa se plantean al inspeccionar el problema o afirmación a investigar y se establecen dos afirmaciones opuestas concernientes a la media 𝜇. Para el ejemplo, estas dos afirmaciones opuestas son: a) “la resistencia media a la rotura es menor que 925” (𝜇 < 925, la preocupación del fabricante de aviones) y b) “la resistencia media a la rotura es por lo menos 925” (𝜇 ≥ 925, la afirmación del proveedor de remaches y la especificación del fabricante de aviones). NOTA: La ley de tricotomía del álgebra establece que la relación entre dos valores numéricos debe cumplir una de las tres condiciones siguientes: <, = o >. Estas tres posibilidades deben tomarse en cuenta entre las dos hipótesis opuestas a fin de que éstas sean negaciones mutuas. Hipótesis nula Hipótesis alternativa 1. Mayor o igual que (≥) 1) Menor que (<) 2. Menor o igual que (≤) 2) Mayor que (>) 3. Igual a (=) 3) No es igual a (≠) Tabla 1. Las tres posibles afirmaciones de la hipótesis nula y alternativa. El parámetro de interés, la media poblacional 𝜇, está relacionado con el valor 925. La afirmación (a) se convierte en la hipótesis alternativa: 𝑯𝒂 : 𝝁 < 𝟗𝟐𝟓 (La media es menor que 925) Esta afirmación representa la preocupación del fabricante de aviones y establece que “los remaches no cumplen con las especificaciones requeridas”. La afirmación (b) se convierte en la hipótesis nula: 𝑯𝟎 : 𝝁 = 𝟗𝟐𝟓 (La media es por lo menos que 925) Esta hipótesis representa la negación de la preocupación del fabricante de aviones y establece que “los remaches cumplen con las especificaciones requeridas”. NOTA: La hipótesis nula debe escribirse sólo con el signo igual (“se asigna un valor”). Cuando “igual” se junta con “menor que” o con “mayor que”, el signo combinado se escribe al lado de la hipótesis nula como recordatorio de que los tres signos han sido tomados en cuenta para escribir estas dos afirmaciones opuestas. Paso 3: Especificar los criterios de la prueba. a. Comprobar los supuestos Las variables como la resistencia a la rotura suelen tener una distribución en forma de montículo; en consecuencia, un tamaño de muestra de 50 debe ser suficientemente; en consecuencia, un tamaño de muestra de 50 debe ser suficientemente grande como para aplicar el Teorema del Límite Central. Puede esperarse que la distribución muestral de medias muestrales esté distribuida normalmente. b. Identificar de prueba a utilizar. Para una prueba de hipótesis de 𝜇, se desea comparar el valor de la media muestral con el valor de la media poblacional, según establece la hipótesis nula. Como estadística de prueba se usará 𝑥̅ −𝜇 𝜎/√𝑛 y se denominará z* (“z estrella”). Se denomina z porque se espera que tenga una distribución normal estándar cuando la hipótesis nula sea verdadera y se cumplan los supuestos. La *(“estrella”) es un recordatorio de que es el valor calculado de la estadística de prueba. c. Determinar el nivel de significancia, 𝛼. Para ver que está implicado con la determinación de 𝛼, la probabilidad del error de tipo I, para el ejemplo de los remaches, se comienza por identificar los cuatro resultados posibles, su significado y la acción relacionada con cada uno. El error de tipo I ocurre cuando se rechaza una hipótesis nula verdadera. Esto sucede cuando el fabricante prueba los remaches que cumplen con las especificaciones y los rechaza. Indudablemente, esto provocaría que los remaches no fuesen comprados aun cuando cumpliesen con las especificaciones. Para que el gerente establezca un nivel de confianza, se requiere información relacionada; a saber, ¿Qué tan pronto se requiere el siguiente suministro de remaches? Si se necesitan mañana y éste es el único vendedor con surtido en existencias, esperar una semana para encontrar remaches aceptables podría ser muy costoso; en consecuencia, rechazar los remaches en buen esto podría considerarse un grave error. Por otra parte, si los remaches no se requieren sino hasta el próximo mes, entonces este error puede no ser tan grave. Sólo el gerente conoce todas las ramificaciones, y así la entrada del gerente es importante aquí. Luego de muchas consideraciones, el gerente asigna 𝛼 = 0.05 como el nivel de significancia. Paso 4: Recolectar y presentar los hechos muestrales. a. Recolectar la información muestral. Ahora ya es posible abordar los datos. La muestra debe seleccionarse de manera aleatoria, extraída de la población cuya media 𝜇 está siendo cuestionada. Se escoge una muestra aleatoria de 50 remaches, se prueba cada uno y se calcula la resistencia media a la rotura de dicha muestra. ̅ = 𝟗𝟐𝟏. 𝟏𝟖 𝒙 𝒚 𝒏 = 𝟓𝟎 b. Calcular el valor de la estadística de prueba. A continuación, los hechos muestrales (𝑥̅ ) se convierten en el valor calculado de la estadística de prueba, z* 𝑧 ∗= ̅ − 𝜇 921.18 − 925.0 𝑥 −3.82 = = −1.5006 = −𝟏. 𝟓𝟎 𝜎 : 18 2.5456 √𝑛 √50 c. Calcular el valor-p. VALOR-PROBABILIDAD O VALOR-P La probabilidad de que la estadística de prueba pueda ser el valor que es o sea un valor más extremo (en la dirección de la hipótesis alternativa) cuando la hipótesis nula es verdadera. Se traza un diagrama de la distribución normal estándar y se ubica z* en él. Para identificar el área que representa el valor-p, observe el signo en la hipótesis alternativa. Para esta prueba, la hipótesis alternativa indica que se tiene interés en aquella parte de la distribución muestral que es “menor que” z*. Por tanto, el valor-p es el área que está a la izquierda de z*. Se sombre esta área. Para encontrar su valor, hay dos opciones: 1. Puede usarse la tabla 3 del apéndice B y calcularlo: El valor-p = 𝑃(𝑧 < 𝑧 ∗) = 𝑃(𝑧 < −1.50) = 𝑃(𝑧 > 1.50) = 0.5000 − 0.4332 = 𝟎. 𝟎𝟔𝟔𝟖 O bien. 2. Pueden usarse la tabla 5 del apéndice B y la propiedad de simetría. Dicha tabla está dispuesta para permitir leer directamente el valor-p, así se ahorra el trabajo que típicamente realiza la computadora. Debido a que 𝑃(𝑧 < −1.50) = 𝑃(𝑧 > 1.50), simplemente se busca z*=1.50 en la tabla 5 y se encuentra que el valor p es 0.0668. Paso 5: Determinar los resultados. a. Determinar si el valor-p es menor o no a 𝛼. El valor-p (0.0688) es mayor que 𝛼(0.05). b. Tomar una decisión sobre 𝐻0 . ¿El valor-p es suficientemente pequeño para indicar que los hechos muestrales son altamente improbables en caso de que la hipótesis nula sea verdadera? Para tomar la decisión es necesario conocer la regla de decisión. REGLA DE DECISIÓN a. Si el valor-p es menor que o igual al nivel de significancia 𝛼, entonces la decisión debe ser rechazar 𝑯𝟎 . b. Si el valor-p es mayor que el nivel de significancia 𝛼,, entonces la decisión debe ser no rechazar 𝑯𝟎 . Decisión: “No rechazar 𝐻0 . c. Escribir una conclusión sobre 𝐻𝑎 . Conclusión: No hay suficientes hechos al nivel de significancia 0.05 que demuestren que la resistencia media a la rotura de los remaches sea menor que 925. “No se condenó” a la hipótesis nula. En otras palabras, es probable que ocurra una media de la muestra tan pequeña como 921.18 (según está definida por 𝛼) cuando el valor verdadero de la media poblacional es 925.0 y 𝑥̅ esté distribuida normalmente. La acción resultante que debe emprender el gerente es comprar los remaches. NOTA: Cuando se llega a la decisión de “no rechazar 𝐻0 ” sólo significa “debido a la falta de mejor información, actúe como si la hipótesis nula fuese verdadera”. Determinación de valores-p Valor-p en la cola derecha Caso 1 𝐻𝑎 contiene “>” “Cola derecha” El valor-p es el área a la derecha de z* valor-p = P (z > z*) Valor-p en la cola izquierda Caso 2 𝐻𝑎 contiene “<” “Cola izquierda” El valor-p es el área a la izquierda de z* El área de la cola izquierda es igual al área de la cola derecha limitada por z*; en consecuencia valor-p = P (z < z*) = 𝑃(𝑧 > |𝑧 ∗ |) Valor-p en ambas colas Caso 3 𝐻𝑎 contiene “≠” “Dos colas” El valor-p es el área total de ambas colas Valor-p P (z < -|z*|) + 𝑃(𝑧 > |𝑧 ∗ |) Debido a que ambas áreas son iguales, se encuentra la probabilidad de una cola y se duplica. Así, el valor-p 2 x 𝑃(𝑧 > |𝑧 ∗ |) Ejemplo 2. Muchas de las grandes compañías de una ciudad han usado durante años a la Kelley Employment Agency para examinar a sus posibles empleados. La prueba de selección que se aplica históricamente ha proporcionado puntajes que se distribuyen de manera normal alrededor de una media de 82 y una desviación estándar de 8. La Brown Agency ha desarrollado una nueva prueba que es más rápida y fácil de administrar, por lo que es menos costosa. Brown afirma que los resultados de su prueba son los mismos obtenidos por Kelley. Muchas de las compañías están considerando un cambio de la Kelley Agency a la Brown Agency para reducir costos. Sin embargo, no desean hacer el cambio si los resultados de la prueba Brown tienen un valor medio diferente. Una empresa de pruebas independiente probó a 36 posibles empleados. Se obtuvo una media de la muestra igual a 79. Determine el valor-p asociado con esta prueba de hipótesis (suponga 𝜎 = 8) Solución Paso 1: Parámetro de interés: la media de todos los puntajes de la prueba, usando el método de la Brown Agency. Paso 2: Las hipótesis: los resultados de la Brown Agency serán diferentes (la preocupación) si el puntaje medio de la prueba no es igual a 82, serán los mismos si la media es igual a 82. En consecuencia, 𝑯𝟎 : 𝝁 = 𝟖𝟐 (los resultados de la prueba tienen la misma media) 𝑯𝟎 : 𝝁 = 𝟖𝟐 (los resultados de la prueba tienen una media diferente) Paso 3: Los criterios de prueba a. Los supuestos: si los puntajes de la prueba Brown están distribuidos de igual forma que los puntajes Kelley, entonces se distribuyen normalmente y la distribución muestral será normal para todos los tamaños de muestra. b. La estadística de prueba: la estadística de prueba será z*. c. El nivel de significancia se omite cuando se pide el valor-p y no por una decisión. Paso 4: Los hechos muestrales. a. Información muestral: n=36, 𝑥̅ = 79 b. Estadística de prueba calculada: 𝑧 ∗= 𝑥̅ − 𝜇 79 − 82 −3 : 𝑧 ∗= = = −𝟐. 𝟐𝟓 𝜎 8 1.3333 √𝑛 √36 c. El valor-p: debido a que la hipótesis alternativa indica una prueba de dos colas, es necesario encontrar la probabilidad asociada de ambas. El valor-p se encuentra al duplicar el área de una cola. Debido a que z*=-2.25, el valor de |z*|=2.25. Así, el valor-p = 2 x P (z > |z*|) = 2 x P (z > 2.25) Usando la tabla 3: valor-p = 2 x P (z > 2.25) = 2 x P (0.5000 – 0.4878) = 2 x (0.0122) = 0.0244 Usando la tabla 5: valor-p = 2 x P (z > 2.25) = 2 x (0.012) o aproximado 0.024 Paso 5: Los resultados. Cuando se pide por el valor-p y no una decisión, el primero es el resultado. El valor-p para esta prueba de hipótesis es de 0.0244. Las compañías no harán una decisión sobre si a) continuarán usando los servicios de Kelley o b) cambarán a la Brown Agency. Cada empresa requiere establecer el nivel de significancia que mejor se adapte a su propia situación y entonces tomar una opción aplicando la regla de decisión antes descrita. La idea de un valor-p es expresar un grado de confianza en la hipótesis nula: a) cuando el valor-p es minúsculo (algo como 0.0003) la 𝐻0 debe ser rechazada por todos porque los resultados muestrales son bastantes improbables para una 𝐻0 verdadera; b) cuando el valor-p es bastante pequeño (como 0.012), los hechos contra 𝐻0 son bastante fuertes y 𝐻0 será rechazada por muchas personas; c) cuando el valor-p comienza a crecer hay muchas probabilidad de que datos como la muestra implicada pueda ocurrir, inclusive si 𝐻0 fuese verdadera, y el rechazo de 𝐻0 no es una decisión fácil de tomar; y d) cuando el valor-p se hace grande, los datos no son en absoluto improbables si 𝐻0 es verdadera, y así nadie rechazará 𝐻0 . Las ventajas del método del valor-p son: 1) los resultados del procedimiento de prueba se expresan en términos de una escala de probabilidad continua de 0.0 a 1.0, en vez de presentarlos sobre una simple base de “rechazar” o “no rechazar”. 2) un valor-p puede reportarse y el usuario de la información decide sobre la fortaleza de los hechos, según los aplique a su propia situación. 3) Las computadoras pueden realizar todos los cálculos y reportar el valor-p, eliminando así la utilización de las tablas. La desventaja del método del valor-p es la tendencia de la gente a aplazar la determinación del nivel de significancia. No debe permitirse que suceda esto, ya que entonces es posible que alguien establezca el nivel de significancia después del hecho, dejando abierta la posibilidad de que resulte su decisión “preferida”. Esto quizá sólo es importante cuando el valor-p reportado cae en el rango de una “decisión difícil” según fue descrito.