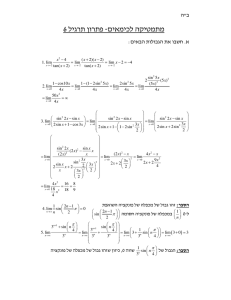
1 דפי נוסחאות בחדו"א גבולות 1 lim arctg = 0 x →∞ x tgx sin x lim = lim =1 x →0 x x → 0 cos x * x sin x lim =1 x →0 x sin x lim =0 x →∞ x x lim =1 x → 0 sin x 1 − cos x lim =0 x →0 x 1 lim = ∞ x →0 x 1 lim − = −∞ x →0 x lim1x = 1 טריגונומטריה cos x cot x = sin x sin x tan x = cos x 1 + cos 2 x cos 2 x = 2 1 − cos 2 x sin 2 x = 2 1 tan 2 A+1= cos 2 A cos(π − α ) = − cos α cos(π + α ) = − cos α sin(π − α ) = sin α sin(π + α ) = − sin α sin(π + α ) = − sin α π sin( x + ) = cos x 2 x→∞ ln(1 + x) =1 x →0 x ex −1 lim =1 x →0 x lim lim arctgx = x →∞ 1 + cos 2 x = 2 cos 2 x 1 − cos 2 x = 2 sin 2 x π sin 2 A+cos 2 A=1 sin 2 A =2sinAcosA 2 lim arctgx = − π x →−∞ lim arctgx = 0 2 x →0 sin(A±B)=sinAcosB±cosAsinB cos(A ± B) =cosAcosB ± sinAsinB cos2A =cos 2 A-sin 2 A =2cos 2 A-1 =1-2sin 2 A גבולות אוילר 1 lim(1 + ) x = e x →∞ x 1 x lim(1 − ) = e −1 x →∞ x 1 lim(1 + x) x = e x →0 1 1 lim(1 − ) x = x →0 x e lim(1 − x) x →0 − 1 x =e 2sinAcosB =sin(A+B) + sin(A-B) 2cosAcosB=cos(A-B)+cos(A+B) 2sinAsinB =cos(A-B)-cos(A+B) cos (α ± β ) = cos α ⋅ cos β ± sin α ⋅ sin β sin (α ± β ) = sin α ⋅ cos β ± cos α ⋅ sin β sin x +π x −π x −π = sin 2 sin 2 2 2 ∞ 1 = ∞* = ∞ *∞ = ∞ 0 0 [email protected] אודי חקים טריגונומטריה המשך... 1 ⎦⎤ ) cos α ⋅ cos β = ⋅ ⎡⎣cos (α − β ) + cos (α + β 2 1 ⎦⎤ ) sin α ⋅ sin β = ⋅ ⎡⎣ cos (α − β ) − cos (α + β 2 1 ⎦⎤ ) sin α ⋅ cos β = ⋅ ⎡⎣sin (α + β ) + sin (α − β 2 1 ⎦⎤ ) cos α ⋅ sin β = ⋅ ⎡⎣sin (α + β ) − sin (α − β 2 α −β ⋅ cos α +β sin α + sin β = 2 ⋅ sin 2 2 α −β α +β sinα -sinβ = 2 ⋅ sin ⋅ cos 2 2 α +β α −β cos α + cos β = 2 ⋅ cos ⋅ cos 2 2 α +β α −β cos α − cos β = −2 ⋅ sin ⋅ sin 2 2 נוסחאות כלליות )( x ± 1) = ( x 2 ± 1)( x 2 + 1 4 )(a 2 − b 2 ) = (a − b)(a + b ) (a ± b) 2 = (a 2 ± 2ab + b 2 −b ± b 2 − 4ac 2a = ax 2 + bx + c → x1,2 זמני מחזור של פונקציות טריגונומטריות ⎫ )⎧sin(ax + b 2π ⎨ = ⎬T a ⎭ )⎩cos(ax + b ⎫ )⎧ tan(ax + b π ⎨ = ⎬T a ⎭ )⎩cot(ax + b משפטים משפט הסנדויץ' bn ≤ an ≤ cn יהיו שתי סדרות\פונקציות תכנסות לגבול מסויים אזי כל סדרה\פונקציה שבינהן תתכנס לאותה גבול. משפט חסימה של 0 תהי סדרה\פונקציה חסומה an ≤ m ו bnסדרה\פונקציה שגבולה 0אזי lim an * bn = 0 ∞→ x תת סדרות תהי סדרה anיש שתי תת סדרות שמתכנסות לגבולות שונים אזי ל anאין גבול. אם כל תת הסדרות של סדרה anמתכנסות לאותו הגבול , Lגבול anהוא גם . L משפט ערך הביניים תהי ) f( xרציפה בקטע סגור ] [a,bו הנקודה C מקיימת ) f ( a ) ≤ C ≤ f ( bאזי קיים לפחות x אחד בקטע ] [a,bשמקיים . f( x ) = C משפט ויירשטראס תהי ) f( xרציפה על קטע סגור ] [a,bהיא מקבלת ערך מקסימלי וערך מינימלי. min ≤ f ( x ) ≤ max הגדרת נגזרת נגדיר פונקציה חדשה ל ) f( xעל הקטע ][a,b ) f ( x ++ x ) − f ( x lim + x→0 +x אם הגבול קיים בכל נקודה פנימית ב ) x ∈ ( a, bאזי הפונקציה היא פונקציית הנגזרת של ) f( xבקטע ][a,b נגזרת של פונקציה הפיכה תהי ) f( xרציפה בסביבות x0והפיכה. אם ) f( xגזירה בנקודה x0ו f ( x ) \ ≠ 0 אזי הפונקציה ההפיכה ) x = g ( yגזירה ב y0 ו אודי חקים [email protected] 1 \ ) f ( x0 = \ ) g( y0 משפטים המשך... נגזרות ) f ′(x ) f (x 0 c rx r −1 xr a x ln a ax ex ex 1 log a x x ln a 1 x ln x )cos(x ) sin( x ) − sin( x )cos(x 1 ) tan(x • אם לא קיים גבול בנקודה x0הפונקציה לא גזירה ב . x0 • פונקציה הגזירה ב x0רציפה ב . x0 • פונקציה שאינה רציפה ב x0אינה גזירה ב . x0 תנאי גזירות L1 = L2 ) = f '( x0 ) + f '( x0 ) − f '( x0 תנאי רציפות = L2 ) = f ( x0 ) − f ( x0 L1 ) + f ( x0 ) f ( xמוגדרת ב x0 סוגי אי רציפות = L2 אי רציפות סליקה≠ f '( x0 ) - ) − f '( x0 אי רציפות קפיצה - ≠ L2 ) − f '( x0 L1 ) + f '( x0 L1 ) + f '( x0 אי רציפות עיקרית L = ∞ / φ - )cos 2 ( x −1 )sin 2 ( x ) cot(x משפט לגרנג' תהי ) f( xמוגדרת ורציפה בקטע ][a,b 1 ) arcsin( x וגזירה ב ) (a,bאזי יש לפחות מספר אחד בקטע ) (a,bשמקיים ). (a<c<b ) f − f( a ) f '( c ) = ( b b−a 1− x2 −1 )arccos(x 1− x2 1 1+ x2 ) arctan( x −1 1+ x2 ) arc cot(x 1 x 2 x U \V − V \U V2 U V \ U \ *V + U *V U *V 1 x2 − אודי חקים [email protected] 1 x משפט רול מקרה פרטי של לגרנג' ,אם בנוסף לתנאי משפט לגרנג' מתקיים ) f ( a ) = f ( bאזי יש לפחות מספר אחד cבקטע ) (a.bשבו . f '( c ) = 0 משפט לופיטל תהיינה ) f( xו ) g( xגזירות בסביבות x = x0 פרט אולי לנקודה עצמה .אזי מתקיימים: אlim f ( x ) = lim g ( x ) = 0 . x →0 ) f '( x = lim x →0 )f( x ב.קיים הגבול ) g ( x ) x → x0 g '( x ניתן להשתמש בלופיטל כאשר יש מצב של ∞ 0 / ∞ 0 lim x → x0 משפטים המשך... אינטגרלים מיידיים ln x + c 1 dx x cx + c ( c ) dx x n +1 +c n +1 x n dx tan x + c 1 cos 2 x − cot x + c 1 dx sin 2 x − cos x + c sin(x ) dx sin x + c cos( x)dx e x dx + c e x dx ax +c ln a קירוב לינארי f ( x) = f ( x0 ) + dy dy = f ' ( x0 ) * dx ) dx = ( x − x0 הערך הכי קרוב שקל לחשב x0 − הערך שצריך לקרב x − טור טיילור f '(x0) *(x−x0)2 f n(x0) *(x−x0)n ' +...+ +Rn f (x)= f(x0) +f (x0) *(x−x0)+ !2 !n אם נתון aהוא מחליף את x0 )( n +1 ) *( x − x0 )( n +1 ) ( x0 f = Rn השגיאה - !)( n + 1 את השגיאה בודקים בין Xל x0בנקודה שהפונקציה ) f ( xמקבלת מקסימום. x a dx 1 dx 1 + x2 arctan x + c dx arcsin x + c 1 1 + x2 1 x−a arctg +c b b dx ⎞⎛ x−a ⎜ arcsin ⎟+c ⎠ ⎝ b 1 dx − ( x − a)2 1 2 +b 2 )∫ ( x − a אינטגרלים שיטת ההצבה f (U ( x ) ) *U (' x ) dx = f (U ( x ) ) + c ∫= I ) - U ( xהחלק המקורי - dUהגזירה של החלק המקורי אינטגרציה בחלקים I = ∫ Udv = U * v − ∫ V * dU - dvהחלק המקורי - vהאינטגרל של dv - Uהחלק המקורי - dUהנגזרת של U אודי חקים [email protected] 2 ∫ (b חקירת פונקציה – אלגוריתם א .תחום הגדרה – שלא יצא בח"מ ב .נקודות חיתוך עם הצירים ג .תחומי עליה וירידה – ע"י נגזרת נקודות קריטיות כאשר הנגזרת מתאפסת וכאשר היא לא מוגדרת. ד .נק' קיצון מקומיות כאשר הנגזרת מתאפסת, הנגזרת לא מוגדרת אבל רציפה או כאשר אן תחום הגדרה. אם נותנים קטע תחום בודקים האם התחומים מאפסים את הנגזרת כדי לבדוק האם הם נקודות קיצון. ה .תחומי קמירות וקעירות ונק' פיתול – ע"י נגזרת שניה כאשר חיובית קמורה וכאשר שלילית קעורה אם שווה אפס יש נקודת פיתול. ו .אסימפטוטות אנכיות – הנק' בהן הפונקציה לא מוגדרת. חוקרים מה קורה להן מימין ומשמאל. ז .אסימפטוטה אופקית – לפי משוואת הקו הישר y = ax + bכאשר: )f ( x a = lim ∞x →± x ) b = lim ( f ( x) − ax ∞x →± אם לא קיים גבול ממשי ,לא קיימת אסימפטוטה.