תרגיל 9 – גבולות (ii)
Anuncio
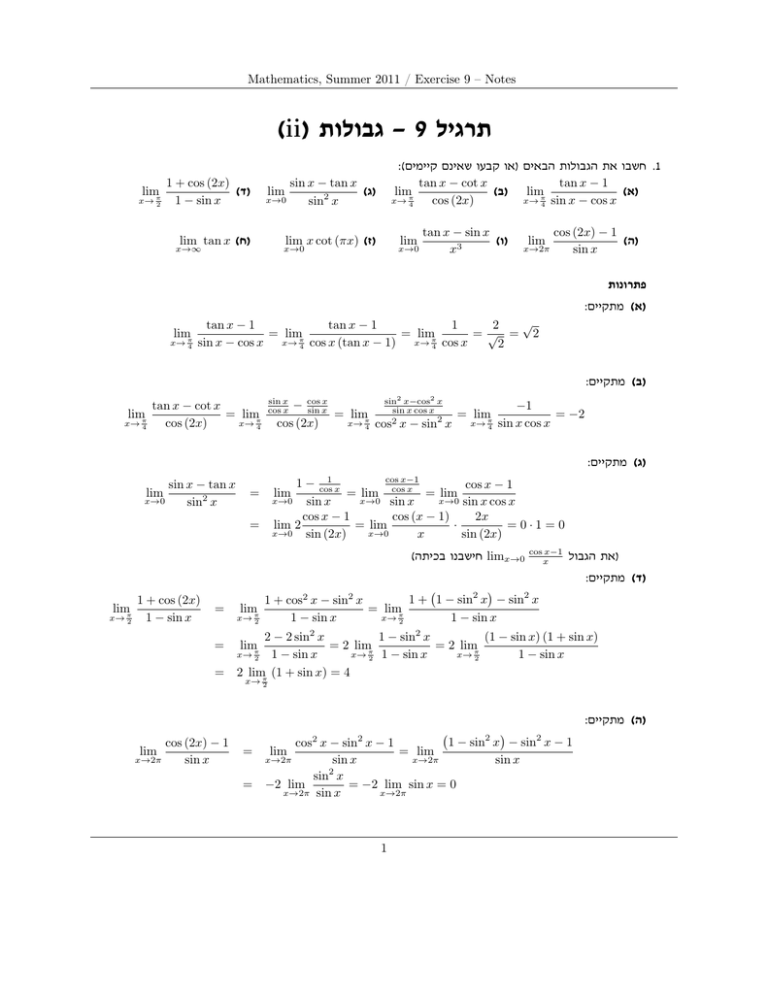
Mathematics, Summer 2011 / Exercise 9 – Notes (ii) – גבולות9 תרגיל lim x→ π 2 1 + cos (2x) ()ד 1 − sin x lim x→0 lim tan x ()ח :( חשבו את הגבולות הבאים )או קבעו שאינם קיימים.1 tan x − cot x tan x − 1 lim ( )בlimπ ()א x→ π x→ cos (2x) sin x − cos x 4 4 sin x − tan x ()ג sin2 x lim x cot (πx) ()ז x→∞ lim x→0 x→0 tan x − sin x ()ו x3 lim x→2π cos (2x) − 1 ()ה sin x פתרונות :)א( מתקיים lim x→ π 4 √ tan x − 1 tan x − 1 1 2 = limπ = limπ =√ = 2 x→ x→ sin x − cos x 2 4 cos x (tan x − 1) 4 cos x :)ב( מתקיים limπ x→ 4 2 sin x cos x 2 x sin x−cos x − cos −1 sin x sin x cos x = limπ = −2 = limπ 2 2 x→ x→ cos (2x) 4 cos x − sin x 4 sin x cos x tan x − cot x = limπ x→ 4 cos (2x) :)ג( מתקיים sin x − tan x x→0 sin2 x lim cos x−1 1 − cos1 x cos x − 1 = lim cos x = lim x→0 x→0 sin x x→0 sin x cos x sin x cos x − 1 cos (x − 1) 2x = lim 2 = lim · =0·1=0 x→0 x→0 sin (2x) x sin (2x) = lim ( חישבנו בכיתהlimx→0 cos x−1 x )את הגבול :)ד( מתקיים limπ x→ 2 1 + cos (2x) 1 − sin x 1 + 1 − sin2 x − sin2 x 1 + cos2 x − sin2 x = limπ x→ 2 1 − sin x 1 − sin x = limπ x→ 2 2 − 2 sin2 x 1 − sin2 x (1 − sin x) (1 + sin x) = 2 limπ = 2 limπ x→ 2 1 − sin x x→ 2 x→ 2 1 − sin x 1 − sin x = 2 limπ (1 + sin x) = 4 = limπ x→ 2 :)ה( מתקיים lim x→2π cos (2x) − 1 sin x 2 = = 1 − sin x − sin2 x − 1 sin x 2 cos x − sin x − 1 = lim x→2π x→2π sin x sin2 x −2 lim = −2 lim sin x = 0 x→2π sin x x→2π lim 1 2 Mathematics, Summer 2011 / Exercise 9 – Notes :()ו( מתקיים )נעזרנו פה בכפל בצמוד lim x→0 tan x − sin x x3 sin x x sin x = lim x→0 x sin x = lim x→0 x = = lim x→0 1 cos x −1 sin x 1 − cos x · 2 x x cos x 1 − cos x 1 + cos x · 2 · x cos x 1 + cos x 1 − cos2 x · 2 x cos x (1 + cos x) · x2 = lim x→0 1 sin x sin2 x 1 1 · · =1·1· = 2 x→0 x x cos x (1 + cos x) 1·2 2 lim :)ז( מתקיים πx cos (πx) 1 · = x→0 sin (πx) π π lim x cot (πx) = lim x→0 .( הנה מחזורית ולא קבועהtan x )ח( גבול זה אינו קיים )הפונקציה :( חשבו את הגבולות הבאים )או קבעו שאינם קיימים.2 √ 1− x−2 sin (3x) 4x2 + 1 √ lim ()ב lim ()ג lim ()א √ 2 x→∞ x→3 x→0 x −9 x−1 x+2− 2 √ lim p x→∞ x4 − 3x2 − 1 − x2 ()ד פתרונות :)א( נוציא גורם משותף בכפייה q x 4+ lim x→∞ 1 x2 x−1 √ √ sin (3x) x+2+ 2 √ ·√ √ lim √ x→0 x+2− 2 x+2+ 2 x = lim · x→∞ x − 1 r 4+ √ 1 =1· 4=2 2 x :)ב( נכפול בצמוד √ √ x+2+ 2 sin 3x · x+2−2 √ √ √ √ sin 3x = lim ·3 x+2+ 2 =1·3·2 2=6 2 x→0 3x = √ 1− x−2 1+ x−2 √ lim · x→3 (x − 3) (x + 3) 1 + x−2 lim x→0 :)ג( נכפול בצמוד √ = = = 1 − (x − 2) √ (x − 3) (x + 3) 1 + x − 2 x−3 √ − lim x→3 (x − 3) (x + 3) 1 + x−2 1 1 1 = √ − lim = x→3 (x + 3) 1 + 6·2 12 x−2 lim x→3 2 Mathematics, Summer 2011 / Exercise 9 – Notes :)ד( נכפול בצמוד √x4 − 3x2 − 1 + x2 p x4 − 3x2 − 1 − x2 · √ x→∞ x4 − 3x2 − 1 + x2 lim x4 − 3x2 − 1 − x4 lim √ x→∞ x4 − 3x2 − 1 + x2 −3x2 − 1 lim q x→∞ 2 x 1 − x32 − x14 + 1 = = −3x2 − 1 ·q x→∞ x2 1− = (−3) · = lim 1 + x→∞ 3x 4 + 2x2 x lim (1 + sin x) sin x ()ג x→0 1 lim (1 + sin x) sin(2x) ()ח lim x→∞ x→0 x+3 x+2 3 x2 − 1 x4 +1 1 3 =− 2 2 :( חשבו את הגבולות הבאים )או קבעו שאינם קיימים.3 x 2x 9 1 lim 1 + ()ב lim 1 + ()א x→∞ x→∞ x 3x 1 ()ד 1 lim 2x lim ()ז x→∞ 2x2 − 1 2x2 + 2 x ()ו 1/x lim (1 + tan (3x)) x→0 ()ה פתרונות :)א( מתקיים lim x→∞ 1 1+ 3x 2x = lim x→∞ 1 1+ 3x 2x 3x ! 3x 2 = e3 :)ב( מתקיים x 1 x !9 9 1 9 lim 1 + = lim 1+ 1 = e9 x→∞ x→∞ x x 9 :)ג( מתקיים lim (1 + sin x) 1 sin x x→0 ,; אבל שניהם יוצאים שווים0אין גבול ב־ 1 sin x ול־ = lim x→0 1+ 1 1 sin x sin1 x =e מאחר, צריך לבדוק פה גבול מימין וגבול משמאל,)למעשה (e וערכם 3 Mathematics, Summer 2011 / Exercise 9 – Notes )ד( מתקיים: 3x 4+2x2 3 = e2 3x2 4+2x2 ·x 4+2x2 3x ∞→limx =e ! x 1 4+2x2 3x = lim 1 + ∞→x 3x 4 + 2x2 lim 1 + ∞→x )ה( מתקיים: )tan(3x x )tan(3x x = elimx→0 כעת נותר לכם לחשב את הגבול 1 )! tan(3x )tan(3x x 1 1 )tan(3x = lim 1 + 1/x x→0 ))lim (1 + tan (3x x→0 limx→0וקיבלתם את התוצאה! )ו(),ז( המטרה היא להעביר את השבר שבפנים לצורה של 1ועוד משהו קטן .נעשה זאת בסעיף זה ו׳ ,ובסעיף ז׳ הפתרון דומה .מתקיים: x 2x2 + 2 − 3 ∞→x 2x2 + 2 x −3 lim 1 + 2 ∞→x 2x + 2 x lim = 2x2 − 1 2x2 + 2 lim ∞→x = ומפה הפתרון כרגיל. )ח( פתרו זאת בעזרת סעיף ג׳ ובעזרת הזהות עבור סינוס של זווית כפולה. .4נתונה הפונקציה )(x + 1) (x − 1 )x (x − 2 = )f (x חשבו את הגבולות הבאים: )א( )lim f (x x→0+ )ד( )lim f (x x→2− )ב( )lim f (x x→0− )ה( )lim f (x ∞→x )ג( )lim f (x x→2+ )ו( )lim f (x ∞x→− פתרונות )א( מתקיים: )1 (x + 1) (x − 1 1 1 · = lim ∞= x x−2 2 x→0+ x lim f (x) = lim x→0+ x→0+ )ב( מתקיים: 1 1 )1 (x + 1) (x − 1 · = lim ∞= − x x−2 2 x→0− x 4 lim f (x) = lim− x→0 x→0− Mathematics, Summer 2011 / Exercise 9 – Notes :)ג( מתקיים lim f (x) = lim+ x→2+ x→2 1 (x − 1) (x + 1) 3 1 · = lim =∞ x−2 x 2 x→2+ x − 2 :)ד( מתקיים lim f (x) = lim− x→2− x→2 1 (x − 1) (x + 1) 3 1 · = lim = −∞ x−2 x 2 x→2− x − 2 :)ה( מתקיים x2 − 1 =1 x→∞ x2 − 2x lim f (x) = lim x→∞ .)ו( בדיוק כמו סעיף ה׳ 5