EJERCICIOS RESUELTOS integrales hoja teoría

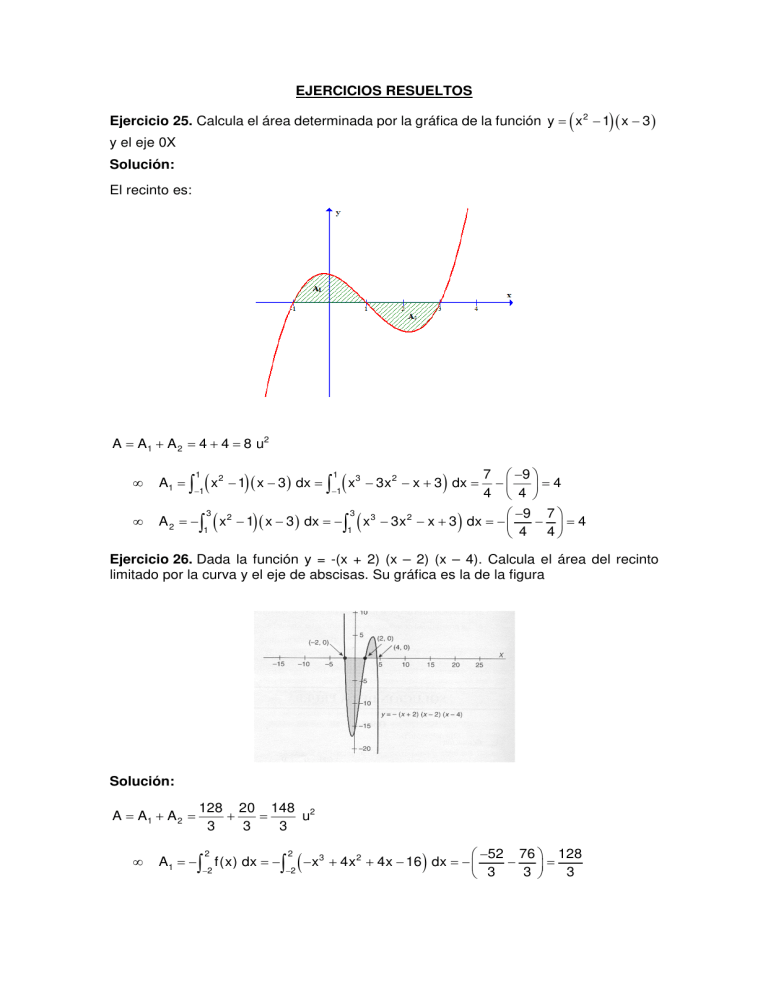
EJERCICIOS RESUELTOS
(
)
Ejercicio 25. Calcula el área determinada por la gráfica de la función y = x 2 − 1 ( x − 3 )
y el eje 0X
Solución:
El recinto es:
A = A 1 + A 2 = 4 + 4 = 8 u2
1
(x
•
A1 = 
•
A 2 = −
−1
3
1
2
(x
)
− 1 ( x − 3 ) dx = 
2
1
−1
)
(x
− 1 ( x − 3 ) dx = − 
3
1
3
)
− 3x 2 − x + 3 dx =
(x
3
7  −9 
−
=4
4  4 
 −9 7 
− 3x 2 − x + 3 dx = − 
− =4
 4 4
)
Ejercicio 26. Dada la función y = -(x + 2) (x – 2) (x – 4). Calcula el área del recinto
limitado por la curva y el eje de abscisas. Su gráfica es la de la figura
Solución:
A = A1 + A 2 =
•
128 20 148 2
+
=
u
3
3
3
2
2
−2
−2
A1 = −  f(x) dx = − 
( −x
3
 −52 76  128
+ 4x 2 + 4x − 16 dx = − 
−
=
3 
3
 3
)
4
4
2
2
A 2 =  f(x) dx = 
•
( −x
3
)
+ 4x 2 + 4x − 16 dx = −
32  −52  20
−
=
3  3  3
Ejercicio 27. Dada la función
x<0
0≤x<3
3≤x≤6
 0

2
3x − x
f(x) = 
 x−3
 0
x>6
Halla el área determinada por f(x), el eje OX y las rectas x = 1 y x = 6. Realiza el dibujo
Solución:
3
(
A =  3x − x
1
2
)
3
6
 3x 2 x 3 
 x2

10 9 47 2
dx +  ( x − 3 ) dx = 
−  +  − 3x  =
+ =
u
3
3 1  2
 2
3 3 2 6
6
Ejercicio 28. Hallar el área de la región del plano limitado por las gráficas f(x)= x3 – x y
g(x) = x 2 .
Solución:
Hallamos los puntos de corte:
x 3 − x = x 2  x 3 − x 2 − x = 0  x = 0, x =
1+ 5
1− 5
,x =
2
2
Sea h(x) = f(x) − g(x) = x 3 − x − x 2
0
A = 1−
2
•
5
(
)
1+ 5
2
0
x3 − x 2 − x dx − 
(x
3
)
− x 2 − x dx = 0,0758 − ( −1,0075 ) = 1,0833 u2
En los cálculos se ha tomado la aproximación:
1+ 5
≈ 1,62
2
1− 5
≈ −0,62
2
Ejercicio 29. Calcular el valor de a>0 para que el área de la región plana acotada por
las gráficas de las curvas y= x3 e y = ax sea igual a 4.
Solución:
Hallamos los puntos de corte:
x 3 = ax  x3 − ax = 0  x = 0, x = a, x = − a
Sea h(x) = x3 − ax
A=
0
− a
(x
3
)
a
− ax dx − 
0
(x
3
)
− ax dx =
a2 2
u
2
a2
= 4  a2 = 8  a = 8 = 2 2
2
Ejercicio 30. Dada la función f(x) = x3 – 12x:
a) Encuentra la primitiva F de f verificando que F(2) = 1
b) Representa gráficamente la función f y calcula el área limitada por la curva y el
eje X entre x = -2 y x = 2.
Solución:
a)
(
)
3
 f(x) dx =  x − 12x dx =
Sea F(x) =
x4
− 6x 2 + C
4
x4
− 6x 2 + C → F ( 2 ) = 4 − 24 + C = 1 → C = 21 . Por lo que la primitiva
4
pedida es F(x) =
x4
− 6x 2 + 21
4
b) La gráfica es:
A=
0
−2
(x
3
)
2
(
)
− 12x dx −  x 3 − 12x dx = 0 − ( −20) − ( −20 − 0) = 40 u2
0
 x 2 − 4x + 3 si x ≤ 1
Ejercicio 31. Se considera la función: f(x) =  2
− x + 4x − 3 si x > 1
a) Estudia la continuidad
b) Representar gráficamente
c) Calcular el área del recinto plano acotado limitado por la gráfica de f, el eje OX,
el eje OY, y la recta x = 2
Solución:
a) Es una función definida a trozos mediante funciones continuas, por lo que tan
solo hay que estudiar la continuidad en x = 1.
•
•
∃f(1) = 0
∃ lím f(x) = 0
x →1
La función es continua en x = 1 y, por tanto, en ℝ
b) El recinto es:
1
(
)
2
(
)
A =  x 2 − 4x + 3 dx +  x 2 − 4x + 3 dx =
0
1
 −2  4   4 2
4
−0+
−  −   = + = 2 u2
3
 3  3  3 3
Ejercicio 32. Sea C(t) el dinero en miles de euros que hay depositado en un día en una
sucursal bancaria, en función del tiempo t en horas desde que la sucursal está abierta.
Sabiendo que C’(t) = t2 – 7t + 10 y que la sucursal permaneció abierta un total de 8
horas:
a) Obtén los máximos y mínimos locales de la función C(t)
b) Obtén la expresión de C(t) sabiendo que a las 6 horas de estar abierta la sucursal
disponía de 20.000€
Solución:
a) C '(t) = 0  t = 5, t = 2 . Estudiando el signo de la derivada, se tiene que el
máximo se alcanza para t = 2 y el mínimo para t = 5.
b) Integrando se tiene que: C(t) =
por lo que C(t) =
t 3 7t 2
−
+ 10t + C . Como C(6) = 20 → C = 14 ,
3
2
t3 7t 2
−
+ 10t + 14
3
2
Ejercicio 33. Calcula el valor de a para que el área del recinto de la figura sea de 36 u2,
siendo la ecuación de la parábola y = x2 – a
Solución: ¡Falta la gráfica!
Ejercicio 34. Dada la función f(x) = (x – 1)·(x + 1)·(x – 3):
a) Calcula una primitiva de f(x)
b) Justifica que F(x) = x4 + 2x – 45 no es primitiva de f(x).
c) Halla el área limitada por la función f(x), el eje OX y las rectas x = 0 y x = 2.
Solución:
3
2
 ( x − 1)( x + 1)( x − 3 ) dx =  ( x − 3x − x + 3 ) dx =
a)
x4
x2
− x3 −
+ 3x
4
2
b) Como F '(x) = 4x 3 + 2 ≠ f(x)  No es una primitiva de f(x).
c) El recinto es:
1
(
)
A =  x 3 − 3x 2 − x + 3 dx − 
0
2
1
(x
3
)
− 3x 2 − x + 3 dx =
7
7  14 2

u
− 0 − 0 −  =
4
4 4

x ≤ −3
2x + 24 si
 2
Ejercicio 35. Dada la función f(x) =  x + 9 si −3 < x ≤ 2
 − x + 15 si
x>2

a) Haz la representación gráfica
b) Calcula la ecuación de la tangente a la gráfica en el punto de abscisa x = 1
c) Calcula el área del recinto plano acotado limitado por la gráfica de f y el eje OX
Solución:
a) La gráfica es:
b) La ecuación de la recta tangente es y − 10 = 2(x − 1) → y = 2x + 8
c) El área es:
A=
−3
−12
( 2x + 24 ) dx + −3 ( x 2 + 9 ) dx + 2 ( − x + 15 ) dx = 81 +
2
15
170 169 1333 2
+
=
u
3
2
6
si
x ≤ −3
 1

2
Ejercicio 36. Dada la función f(x) =  ( x + 1) si −3 < x < 1 se pide:
 −4x + 8 si
x ≥1

a) Dibuja su gráfica
b) Estudia su continuidad en x = -3 y en x = 1
c) Calcula el área del recinto plano delimitado por la gráfica de la función y el eje
horizontal
Solución:
a) La gráfica es:
b) Continuidad en x = - 3
1) ∃ f( −3) = 1
2) ¿ ∃ lím f(x)?
x →−3
lím f(x) = lím− 1 = 1


 ∃ lím f(x)  Presenta una discontinuidad

2
x → -3
lím+ f(x) = lím+ (x + 1) = 4 
x →−3
x →−3

inevitable de salto 3.
x →−3−
x →−3
Continuidad en x = 1
1) ∃ f(1) = 4
2) ¿ ∃ lím f(x)?
x →1
( x + 1)
= 4 
f(x) = 4 
  ∃ lím
x→ 1
lím+ f(x) = lím+ ( −4x + 8) = 4 
x →1
x →1

Como f(1) = lím f(x) = 4  f(x) es continua en x = 1
lím− f(x) = lím−
x →1
x →1
2
x →1
c) El área es:
A =  (x + 1)2 dx +  ( −4x + 8 ) dx =  (x 2 + 2x + 1) dx +  ( −4x + 8 ) dx =
1
2
−1
1
1
1
−1
2
1
2
 x3

 7  −1  
8
14 2
=  + x 2 + x  +  −2x 2 + 8x  =  −    + ( 8 − 6 ) = + 2 =
u
1
3
3
 3  3 
3
 −1