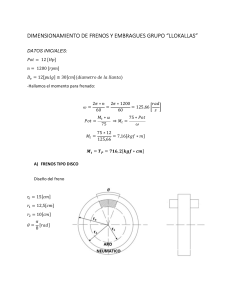
DIMENSIONAMIENTO DE FRENOS Y EMBRAGUES GRUPO “LLOKALLAS” DATOS INICIALES: 𝑃𝑜𝑡 = 12 [𝐻𝑝] 𝑛 = 1200 [𝑟𝑝𝑚] 𝐷 = 12[𝑝𝑢𝑙𝑔] ≅ 30[𝑐𝑚](𝑑𝑖𝑎𝑚𝑒𝑡𝑟𝑜 𝑑𝑒 𝑙𝑎 𝑙𝑙𝑎𝑛𝑡𝑎) -Hallamos el momento para frenado: 𝜔= 2𝜋 ∗ 𝑛 2𝜋 ∗ 1200 𝑟𝑎𝑑 = = 125,66 60 60 𝑠 𝑃𝑜𝑡 = 𝑀 ∗𝜔 75 ∗ 𝑃𝑜𝑡 ⇒𝑀 = 75 𝜔 𝑀 = 75 ∗ 12 = 7,16[𝑘𝑔𝑓 ∗ 𝑚] 125,66 𝑴𝒕 = 𝑻𝑷 = 𝟕𝟏𝟔, 𝟐[𝒌𝒈𝒇 ∗ 𝒄𝒎] A) FRENOS TIPO DISCO Diseño del freno 𝑟 = 15[𝑐𝑚] 𝑟 = 12,5[𝑐𝑚] 𝑟 = 10[𝑐𝑚] 𝜃= 𝜋 [𝑟𝑎𝑑] 8 Escogemos tipo de freno 𝜇 = 0,45 -Trabajaremos modelado como presión constante por tanto las ecuaciones a utilizar serán: 1) 𝐹 = 𝜃 ∗ 𝑃 ∗ 𝜇 ∗ (𝑟 2 −𝑟 ) 2) 𝑇 = 𝜃 ∗ 𝑃 ∗ 𝜇 ∗ (𝑟 3 −𝑟 ) 𝑃 = 3∗𝑇 𝜃 ∗ 𝜇 ∗ (𝑟 − 𝑟 ) De la ecuación 2) hallamos Pa 3 ∗ 716,2 𝑘𝑔𝑓 𝑃 =𝜋 = 12,76 𝑐𝑚 ∗ 0,45 ∗ (12,5 − 10 ) 8 𝑃 = 1251,3[𝑘𝑃𝑎] Verificamos que este en el rango del freno escogido 1030[𝑘𝑃𝑎] < 𝑃 < 2070[𝑘𝑃𝑎] 1030[𝑘𝑃𝑎] < 1251,3[𝑘𝑃𝑎] < 2070[𝑘𝑃𝑎]𝑐𝑢𝑚𝑝𝑙𝑒 Hallamos la fuerza de frenado 𝐹 = 𝐹 = 𝜃 ∗ 𝑃 ∗ 𝜇 ∗ (𝑟 2 −𝑟 ) 𝜋 ∗ 12,76 ∗ 0,45 ∗ (12,5 − 10 ) = 63,42[𝑘𝑔𝑓] 16 Hallamos la presión en el cilindro hidráulico: Sea ∅ = 3[𝑐𝑚] 𝑃 = 𝑃 = 𝐹 𝐹 = 𝜋∗∅ 𝐴 4 63,42 𝑘𝑔𝑓 = 8,97 𝜋∗3 𝑐𝑚 4 Con esta presión hallamos el espesor de pared para el cilindro: Material SAE1020 𝜎 = 2300 𝑛=3 𝜎 ≤ 𝜎 𝑛 𝜎 𝑃∗𝐷 ≤ 2∗𝑒 𝑛 𝑒≥ 𝑒≥ 𝑃∗𝐷∗𝑛 2∗𝜎 8,97 ∗ 3 ∗ 3 2 ∗ 2300 𝑒 ≥ 0,02[𝑐𝑚] B) FRENOS TIPO ZAPATA Diseño del freno 𝑟 = 15[𝑐𝑚] 𝑟 = 12[𝑐𝑚] 𝑐 = 10[𝑐𝑚] 𝑎 = 8,5[𝑐𝑚] 𝑒 = 17[𝑐𝑚] 𝑆 = 1[𝑐𝑚] 𝑏 = 2,5[𝑐𝑚] 𝑟 = 10,75[𝑐𝑚] Hallamos 𝜃 y 𝜃 Hallamos 𝛽 tan(𝛽 ) = 𝑒⁄2 ⇒ 𝛽 = tan 𝑐 ⁄2 𝑒 𝑐 17 = 59,5° = 1,04[𝑟𝑎𝑑] 10 𝛽 = tan Hallamos 𝛽 tan(𝛽 ) = 𝛽 = tan 𝜽𝟏 = 𝑎 ⇒ 𝛽 = tan 𝑐 ⁄2 2𝑎 𝑐 2 ∗ 8,5 = 59,5° = 1,04[𝑟𝑎𝑑] 10 𝑆 1 = = 𝟎, 𝟎𝟖𝟑[𝒓𝒂𝒅] = 𝟒, 𝟕𝟓° 𝑟 12 𝜃 =𝜋−𝜃 −𝛽 −𝛽 𝜽𝟐 = 𝜋 − 0,083 − 1,04 − 1,04 = 𝟎, 𝟗𝟖[𝒓𝒂𝒅] = 𝟓𝟔° Escogemos tipo de freno 𝜇 = 0,45 Analizamos para la parte derecha (auto energizante) Sea: 𝑇 𝑇 ≈ 0,7 ∗ 𝑇 = 0,7 ∗ 716,2 = 501,34[𝑘𝑔𝑓 ∗ 𝑐𝑚] Además, conocemos la ecuación: 𝑇 = 𝜇∗𝑃 ∗𝑏∗𝑟 ∗ (cos 𝜃 − cos 𝜃 ) sin 𝜃 Además, como 𝜃 ≤ 90° ⇒ 𝜃 = 𝜃 Hallamos 𝑃 𝑃 𝑃 = = 𝑇 𝜇∗𝑏∗𝑟 ∗ sin 𝜃 ∗ (cos 𝜃 − cos 𝜃 ) 501,34 ∗ sin 56 0,45 ∗ 2,5 ∗ 12 ∗ (cos 4,75 − cos 56) 𝑃 = 5,87 𝑃 𝑘𝑔𝑓 𝑐𝑚 = 575,16[𝑘𝑃𝑎] Verificamos que este en el rango del freno escogido 𝑃 < 1030[𝑘𝑃𝑎] 575,16[𝑘𝑃𝑎] < 1030[𝑘𝑃𝑎] 𝑠𝑖 𝑐𝑢𝑚𝑝𝑙𝑒 Analizamos para la parte izquierda (no auto energizante) Sea: 𝑇 ≈ 0,3 ∗ 𝑇 𝑇 = 0,3 ∗ 716,2 = 214,86[𝑘𝑔𝑓 ∗ 𝑐𝑚] Además, conocemos la ecuación: 𝑇 = 𝜇∗𝑃 ∗𝑏∗𝑟 ∗ (cos 𝜃 − cos 𝜃 ) sin 𝜃 Además, como 𝜃 ≤ 90° ⇒ 𝜃 = 𝜃 Hallamos 𝑃 𝑃 𝑃 𝑇 = = 𝜇∗𝑏∗𝑟 ∗ sin 𝜃 ∗ (cos 𝜃 − cos 𝜃 ) 214,86 ∗ sin 56 0,45 ∗ 2,5 ∗ 12 ∗ (cos 4,75 − cos 56) 𝑃 𝑃 = 2,51 𝑘𝑔𝑓 𝑐𝑚 = 246,15[𝑘𝑃𝑎] Hallamos los momentos: -Derecha: 𝑀 𝑀 = = 𝑏∗𝑟 ∗𝑟 ∗𝑃 4 ∗ sin 𝜃 2,5 ∗ 12 ∗ 10,75 ∗ 5.87 ∗ [2(0,98 − 0,083) + sin(2 ∗ 4,75) − sin(2 ∗ 56)] 4 ∗ sin 56 𝑀 𝑀 𝑀 ∗ [2(𝜃 − 𝜃 ) + sin(2𝜃 ) − sin(2𝜃 )] = = = 589,1[𝑘𝑔𝑓 ∗ 𝑐𝑚] 𝑏∗𝑟 ∗𝜇∗𝑃 sin 𝜃 ∗ −𝑟 (cos 𝜃 − cos 𝜃 ) − 𝑟 sin 𝜃 2 2,5 ∗ 12 ∗ 0,45 ∗ 5,87 10,75 ∗ −12(cos 56 − cos 4,75) − sin 56 sin 56 2 𝑀 = 148,6[𝑘𝑔𝑓 ∗ 𝑐𝑚] Para el lado izquierdo 𝑀 𝑃 = 𝑀 𝑃 ⇒𝑀 𝑀 = 𝑀 = 𝑀 ∗𝑃 𝑃 589,1 ∗ 2,51 5,87 = 251,9[𝑘𝑔𝑓 ∗ 𝑐𝑚] 𝑀 𝑃 = 𝑀 𝑃 ⇒𝑀 𝑀 = 𝑀 = 𝑀 ∗𝑃 𝑃 148,6 ∗ 2,51 5,87 = 63,5[𝑘𝑔𝑓 ∗ 𝑐𝑚] La fuerza de accionamiento estará dada por: 𝐹= 𝐹= 𝑀 −𝑀 𝑐 589,1 − 148,6 = 44,1[𝑘𝑔𝑓] 10 Hallamos la presión en el cilindro hidráulico: Sea ∅ = 2[𝑐𝑚] 𝑃 = 𝑃 = 𝐹 𝐹 = 𝐴 𝜋∗∅ 4 44,1 𝑘𝑔𝑓 = 14 𝜋∗2 𝑐𝑚 4 Con esta presión hallamos el espesor de pared para el cilindro: Material SAE1020 𝜎 = 2100 𝑛=3 𝜎 ≤ 𝜎 𝑛 𝑃∗𝐷 𝜎 ≤ 2∗𝑒 𝑛 𝑒≥ 𝑃∗𝐷∗𝑛 2∗𝜎 𝑒≥ 14 ∗ 2 ∗ 3 2 ∗ 2100 𝑒 ≥ 0,02[𝑐𝑚] Dimensionamos los pasadores (corte) Hallamos las reacciones en el lado derecho (más crítico): Pero sabemos que: 𝑅 = cos 𝜃 𝑑𝑁 − 𝑅 = 𝜇cos 𝜃 𝑑𝑁 − ∗ ∗ 𝑑𝑁 = 𝜇 sin 𝜃 𝑑𝑁 − 𝐹 sin 𝜃 𝑑𝑁 − 𝐹 𝑑𝜃 𝑅 = 𝑃 ∗ 𝑏 ∗ 𝑟 sin 𝜃 ∗ cos 𝜃 𝑑𝜃 − sin 𝜃 𝑅 = 𝑃 ∗ 𝑏 ∗ 𝑟 sin 𝜃 ∗ 𝜇cos 𝜃 𝑑𝜃 − sin 𝜃 𝑃 ∗ 𝑏 ∗ 𝑟 sin 𝜃 ∗ 𝜇 sin 𝜃 𝑑𝜃 − 𝐹 sin 𝜃 𝑃 ∗ 𝑏 ∗ 𝑟 sin 𝜃 ∗ sin 𝜃 𝑑𝜃 − 𝐹 sin 𝜃 Integrando tenemos: 𝑅 = 𝑅 = 𝑅 = 𝑃 ∗𝑏∗𝑟 sin 𝜃 sin 𝜃 ∗ cos 𝜃 𝑑𝜃 − 𝑃 ∗ 𝑏 ∗ 𝑟 sin 𝜃 sin 𝜃 − sin 𝜃 2 2 − 𝑃 ∗𝑏∗𝑟 ∗𝜇 sin 𝜃 sin 𝜃 𝑑𝜃 − 𝐹 𝑃 ∗𝑏∗𝑟 ∗𝜇 𝜃 sin 2𝜃 𝜃 sin 2𝜃 − − + sin 𝜃 2 4 2 4 −𝐹 5,87 ∗ 2,5 ∗ 12 sin 56 sin 4,75 5,87 ∗ 2,5 ∗ 12 ∗ 0,45 0,98 sin 2 ∗ 56 0,083 sin 2 ∗ 4,75 − − − − + − 44,1 sin 56 2 2 sin 56 2 4 2 4 𝑅 = 3,51[𝑘𝑔𝑓] 𝑅 = 𝑅 = 𝑃 ∗𝑏∗𝑟 ∗𝜇 sin 𝜃 sin 𝜃 ∗ cos 𝜃 𝑑𝜃 − 𝑃 ∗ 𝑏 ∗ 𝑟 ∗ 𝜇 sin 𝜃 sin 𝜃 − sin 𝜃 2 2 − 𝑃 ∗𝑏∗𝑟 sin 𝜃 sin 𝜃 𝑑𝜃 − 𝐹 𝑃 ∗𝑏∗𝑟 𝜃 sin 2𝜃 𝜃 sin 2𝜃 − − + sin 𝜃 2 4 2 4 −𝐹 𝑅 = 5,87 ∗ 2,5 ∗ 12 ∗ 0,45 sin 56 sin 4,75 5,87 ∗ 2,5 ∗ 12 0,98 sin 2 ∗ 56 0,083 sin 2 ∗ 4,75 − − − − + −0 sin 56 2 2 sin 56 2 4 2 4 𝑅 = −22,3[𝑘𝑔𝑓] Finalmente hallamos la resultante: 𝑅= 𝑅 𝑅= +𝑅 22,3 + 3,51 𝑅 = 22,6[𝑘𝑔𝑓] Y dimensionamos al corte SAE1020 𝜎 = 3569 𝑛=3 𝜏 ≤ 𝜏̅ 0,5𝜎 𝑅 ≤ 𝜋∗∅ 𝑛 4 ∅≥ ∅≥ 4𝑅 ∗ 𝑛 𝜋 ∗ 0,5𝜎 4 ∗ 22,6 ∗ 3 𝜋 ∗ 0,5 ∗ 3569 ∅ ≥ 0,22[𝑐𝑚] C) FRENOS TIPO CINTA DATOS INICIALES: 𝑃𝑜𝑡 = 12 [𝐻𝑝] 𝑛 = 1200 [𝑟𝑝𝑚] 𝐷 = 12[𝑝𝑢𝑙𝑔] ≅ 30[𝑐𝑚](𝑑𝑖𝑎𝑚𝑒𝑡𝑟𝑜 𝑑𝑒 𝑙𝑎 𝑙𝑙𝑎𝑛𝑡𝑎) 𝑠𝑒𝑛𝑡𝑖𝑑𝑜 𝑑𝑒 𝑔𝑖𝑟𝑜: ℎ𝑜𝑟𝑎𝑟𝑖𝑜 -Hallamos el momento para frenado: 𝜔= 2𝜋 ∗ 𝑛 2𝜋 ∗ 1200 𝑟𝑎𝑑 = = 125,66 60 60 𝑠 𝑃𝑜𝑡 = 𝑀 ∗𝜔 75 ∗ 𝑃𝑜𝑡 ⇒𝑀 = 75 𝜔 𝑀 = 75 ∗ 12 = 7,16[𝑘𝑔𝑓 ∗ 𝑚] 125,66 𝑴𝒕 = 𝟕𝟏𝟔, 𝟐[𝒌𝒈𝒇 ∗ 𝒄𝒎] Diseño del freno 𝑏 = 50 [𝑚𝑚] 𝑎𝑛𝑐ℎ𝑜 𝑛𝑜𝑟𝑚𝑎𝑙𝑖𝑧𝑎𝑑𝑜 𝑑𝑒 𝑙𝑎 𝑐𝑖𝑛𝑡𝑎 𝑙 = 500 [𝑚𝑚] 𝑙 = 150 [𝑚𝑚] 𝜃 = 𝜋 + 𝛼 [𝑟𝑎𝑑] 𝛼 = tan 𝛼 = tan 𝑙 𝑙 150 = 17° 500 𝛼 = 0,3[𝑟𝑎𝑑] 𝜃 = 𝜋 + 0,3 = 3,438 [𝑟𝑎𝑑] Escogemos material 𝜇 = 0,45 𝑃 = (345 − 690)[𝐾𝑃𝑎] Determinamos las fuerzas en el freno: 𝑀𝑡 = (𝐹1 − 𝐹2) ∗ 𝐷 2 𝐹1 = 𝐹2 ∗ 𝑒 2 ecuaciones 2 incógnitas: 716,2 = (𝐹1 − 𝐹2) ∗ 𝐹1 = 𝐹2 ∗ 𝑒 , 30 2 ∗ , 𝐹2 = 12,91[𝑘𝑔𝑓] 𝐹1 = 60,65 [𝑘𝑔𝑓] Determinamos la presión máxima en la cinta: 𝑃𝑚𝑎𝑥 = 𝑃𝑚𝑎𝑥 = 60,65 5 ∗ 15 𝐹1 𝑎∗𝑅 = 0,81[𝑘𝑔𝑓 ⁄𝑐𝑚 ] 𝑃𝑚𝑎𝑥 = 79,4[𝐾𝑃𝑎] Verificamos que este en el rango del freno escogido 𝑃 < 345[𝑘𝑃𝑎] 79,4[𝐾𝑃𝑎] < 345[𝑘𝑃𝑎] Hallamos la fuerza a aplicar en la palanca: 𝑙 = 150 [𝑚𝑚] 𝑙 = 400 [𝑚𝑚] 𝐹1 = 60,15[𝑘𝑔𝑓] ∑𝑀 = 0 −𝐹 ∗ 𝑙 + 𝐹 (𝑙 + 𝑙 ) = 0 𝐹 = 𝐹 = 𝐹 ∗𝑙 (𝑙 + 𝑙 ) 60,15 ∗ 150 (150 + 400) 𝐹 = 16[𝑘𝑔𝑓] Dimensionamos el pasador al corte: 𝐹2 = 12,91 [𝑘𝑔𝑓] SAE1010 𝜎 = 2100 𝑛=3 𝜏 ≤ 𝜏̅ 0,5𝜎 𝐹2 ≤ 𝜋∗∅ 𝑛 4 ∅≥ ∅≥ 4 ∗ 𝐹2 ∗ 𝑛 𝜋 ∗ 0,5𝜎 4 ∗ 12,91 ∗ 3 𝜋 ∗ 0,5 ∗ 2100 ∅ ≥ 0,22[𝑐𝑚] DIMENSIONAMIENTO DE RESORTES GRUPO “LLOKALLAS” DATOS INICIALES: 𝐹 = 44,1[𝑘𝑔𝑓] 𝑐 = 10[𝑐𝑚] 𝑎 = 2[𝑐𝑚] Hallamos la fuerza sobre el resorte ∑𝑀 = 0 −𝐹 ∗ 𝑐 − 𝐹 (𝑐 − 𝑎 ) = 0 𝐹 = 𝐹 = −𝐹 ∗ 𝑐 (𝑐 − 𝑎 ) −44,1 ∗ 10 (10 − 2) 𝐹 = 55,12[𝑘𝑔𝑓] DIMENSIONAMIENTO A LA ESTATICA Seleccionamos material: SAE 6150 𝜎 = 1020[𝑀𝑃𝑎] = 10401[𝑘𝑔𝑓/𝑐𝑚 ] 𝑛=2 𝜏 ≤ 𝜏̅ 0,5𝜎 8𝐹 ∗ 𝐷 2𝐶 + 1 ∗ ≤ 𝜋∗𝑑 2𝐶 𝑛 4 ≤ 𝐶 ≤ 12 𝑣𝑎𝑙𝑜𝑟 𝑑𝑒𝑙 𝑖𝑛𝑑𝑖𝑐𝑒 𝑑𝑒𝑙 𝑟𝑒𝑠𝑜𝑟𝑡𝑒 sea 𝑪 = 𝟖 𝐶= 𝐷 ⇒𝐷 =𝐶∗𝑑 𝑑 𝐷 = 8𝑑 0,5𝜎 64𝐹 2𝐶 + 1 ∗ ≤ 𝜋∗𝑑 2𝐶 𝑛 𝑑≥ 𝑑≥ 64𝐹 ∗ 𝑛 2𝐶 + 1 ∗ 𝜋 ∗ 0,5𝜎 2𝐶 64 ∗ 55,12 ∗ 2 16 + 1 ∗ 𝜋 ∗ 0,5 ∗ 10401 16 𝑑 ≥ 0,47 𝑐𝑚 sea 𝑪 = 𝟒 𝐶= 𝐷 ⇒𝐷 =𝐶∗𝑑 𝑑 𝐷 = 4𝑑 0,5𝜎 32𝐹 2𝐶 + 1 ∗ ≤ 𝜋∗𝑑 2𝐶 𝑛 𝑑≥ 𝑑≥ 32𝐹 ∗ 𝑛 2𝐶 + 1 ∗ 𝜋 ∗ 0,5𝜎 2𝐶 32 ∗ 55,12 ∗ 2 8+1 ∗ 𝜋 ∗ 0,5 ∗ 10401 8 𝑑 ≥ 0,34 𝑐𝑚 sea 𝑪 = 𝟏𝟎 𝐶= 𝐷 ⇒𝐷 =𝐶∗𝑑 𝑑 𝐷 = 10𝑑 0,5𝜎 80𝐹 2𝐶 + 1 ∗ ≤ 𝜋∗𝑑 2𝐶 𝑛 𝑑≥ 𝑑≥ 80𝐹 ∗ 𝑛 2𝐶 + 1 ∗ 𝜋 ∗ 0,5𝜎 2𝐶 80 ∗ 55,12 ∗ 2 20 + 1 ∗ 𝜋 ∗ 0,5 ∗ 10401 20 𝑑 ≥ 0,53 𝑐𝑚 Elegimos 𝑪 = 𝟖 𝑛𝑜𝑟𝑚𝑎𝑙𝑖𝑧𝑎𝑛𝑑𝑜 𝑑 = 5 [𝑚𝑚] DIMENSIONAMIENTO A LA FATIGA 𝐹 = 44,1[𝑘𝑔𝑓] 𝐹 = 0[𝑘𝑔𝑓] 𝜎 = 1020[𝑀𝑃𝑎] = 10401[𝑘𝑔𝑓/𝑐𝑚 ] SAE 6150 𝜎 = 1082[𝑀𝑃𝑎] = 11033[𝑘𝑔𝑓/𝑐𝑚 ] 𝑛=3 𝑃 = 𝑃 = 𝑠𝑒𝑎 𝐶 = 8 −𝐹 2 55,12 − 0 = 27,6[𝑘𝑔𝑓] 2 𝑃 = 𝑃 = 𝐹 𝐹 +𝐹 2 55,12 + 0 = 27,6[𝑘𝑔𝑓] 2 𝐶= 𝐷 ⇒𝐷 =𝐶∗𝑑 𝑑 𝐷 = 8𝑑 𝜏 = 8𝑃 ∗ 𝐷 4𝐶 − 1 0,615 ∗ + 𝜋∗𝑑 4𝐶 − 4 𝐶 𝜏 = 64𝑃 4𝐶 − 1 0,615 ∗ + 𝜋∗𝑑 4𝐶 − 4 𝐶 𝜏 = 64 ∗ 27,6 32 − 1 0,615 ∗ + 𝜋 ∗ 0,5 32 − 4 8 𝜏 = 2662,9 𝜏 = 8𝑃 ∗ 𝐷 4𝐶 − 1 0,615 ∗ + 𝜋∗𝑑 4𝐶 − 4 𝐶 𝜏 = 𝜏 = 𝑘𝑔𝑓 𝑐𝑚 64𝑃 4𝐶 − 1 0,615 ∗ + 𝜋∗𝑑 4𝐶 − 4 𝐶 64 ∗ 27,6 32 − 1 0,615 ∗ + 𝜋 ∗ 0,5 32 − 4 8 𝜏 = 2662,9 𝑘𝑔𝑓 𝑐𝑚 𝜏 𝜏 1 + ≤ 𝑆 𝑆 𝑛 Factores de Marin 𝑆 = 1082[𝑀𝑃𝑎] -Factor de condicion superficial: 𝑲𝒂 = 𝒂 ∗ 𝑺𝒖𝒕 𝒃 “Diseño en Ingeniería Mecánica de Shigley” Pág. 280 𝑎 = 4,51 𝑏 = −0,265 𝐾 = 4,51 ∗ 1082 , 𝐾 = 0,71 -Factor de tamaño: “Diseño en Ingeniería Mecánica de Shigley” Pág. 280 𝐾 = 1,51𝑑 , = 1,51(5) 𝐾 = 1,27 -Factor de carga: “Diseño en Ingeniería Mecánica de Shigley” Pág. 282 𝐾 = 0,59 -Factor de temperatura: “Diseño en Ingeniería Mecánica de Shigley” Pág. 283 Temperatura de trabajo = 20 ºC , 𝐾 = 𝑆 =1 𝑆 -Factor de confiabilidad: “Diseño en Ingeniería Mecánica de Shigley” Pág. 282 90% de confiabilidad 𝐾 = 0,897 -Factor de efectos varios: 𝐾𝑓 = 1 Finalmente tenemos: 𝑺𝒆 = 𝑲 𝒂 ∗ 𝑲 𝒃 ∗ 𝑲 𝒄 ∗ 𝑲 𝒅 ∗ 𝑲 𝒆 ∗ 𝑲 𝒇 ∗ 𝑺 𝒆 ` 𝑆 ` = 0,5𝑆 = 0,5 ∗ 11033 𝑘𝑔𝑓 𝑘𝑔𝑓 = 5516,5 𝑐𝑚 𝑐𝑚 𝑆 = 0,71 ∗ 1,27 ∗ 0,59 ∗ 1 ∗ 0,897 ∗ 1 ∗ 5516,5 𝑆 = 2632,5 𝑘𝑔𝑓 𝑐𝑚 Reemplazando en la fórmula de Goodman 𝜏 𝜏 1 + ≤ 𝑆 𝑆 𝑛 2662,9 2662,9 1 + ≤ 10401 2632,5 3 0,247 ≤ 0,33 𝑐𝑢𝑚𝑝𝑙𝑒 𝑙𝑎 𝑑𝑒𝑠𝑖𝑔𝑢𝑎𝑙𝑑𝑎𝑑 𝑝𝑜𝑟 𝑡𝑎𝑛𝑡𝑜 𝑑 = 5 [𝑚𝑚] DIMENSIONAMIENTO DE LA LONGITUD DATOS 𝐹 = 55,12[𝑘𝑔𝑓] 𝐶=8 𝑑 = 5 [𝑚𝑚] 𝑒𝑥𝑡𝑟𝑒𝑚𝑜 𝑠𝑖𝑚𝑝𝑙𝑒 𝜎 = 1020[𝑀𝑃𝑎] = 10401[𝑘𝑔𝑓/𝑐𝑚 ] Material SAE 6150 𝜎 = 1082[𝑀𝑃𝑎] = 11033[𝑘𝑔𝑓/𝑐𝑚 ] 𝐸 = 2,1𝑥10 [𝑘𝑔𝑓/𝑐𝑚 ] 𝜇 = 0,3 𝑐 = 10[𝑐𝑚] = 100[𝑚𝑚] 𝑎 = 2[𝑐𝑚] = 20[𝑚𝑚] 𝑏 = 3[𝑐𝑚] = 30[𝑚𝑚] 𝛿 = 5[𝑚𝑚] -Hallamos el desplazamiento angular 𝛼 de la zapata 𝛿 𝑐 𝛼 = tan = tan 5 100 𝛼 = 3° = 0,052[𝑟𝑎𝑑] ℎ𝑎𝑙𝑙𝑎𝑚𝑜𝑠 𝑙𝑎 𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎 𝑟𝑎𝑑𝑖𝑎𝑙 𝑐 𝑑𝑒𝑙 𝑝𝑎𝑠𝑎𝑑𝑜𝑟 𝑎𝑙 𝑒𝑥𝑡𝑟𝑒𝑚𝑜 𝑑𝑒𝑙 𝑟𝑒𝑠𝑜𝑟𝑡𝑒 𝑐 = (𝑐 − 𝑎 ) + 𝑏 (100 − 20) + 30 𝑐 = 𝑐 = 85,44[𝑚𝑚] 𝑙𝑎 𝑑𝑒𝑓𝑜𝑟𝑚𝑎𝑐𝑖𝑜𝑛 𝑚𝑎𝑥𝑖𝑚𝑎 𝑑𝑒𝑙 𝑟𝑒𝑠𝑜𝑟𝑡𝑒 𝑒𝑠𝑡𝑎𝑟𝑎 𝑑𝑎𝑑𝑎 𝑝𝑜𝑟: 𝛿 = 𝛼 ∗ 𝑐 = 0,052 ∗ 85,44 𝛿 = 4,2[𝑚𝑚] Hallamos el número de espiras: 𝑁 = 𝐺∗𝑑 𝐺∗𝑑 = 8 ∗ 𝐷 ∗ 𝑘 8 ∗ (8𝑑) ∗ 𝑘 Hallamos el módulo al corte; 𝐺= 𝐸 2,1𝑥10 = 2(1 + 𝜇) 2(1 + 0,3) 𝐺 = 0,81𝑥10 [𝑘𝑔𝑓/𝑐𝑚 ] Hallamos el coeficiente k del resorte; 𝑘= 𝐹 𝛿 = 55,12 0,42 𝑘 = 131,24[𝑘𝑔𝑓/𝑐𝑚] 𝑁 = 0,81𝑥10 ∗ 0,5 = 2,79 = 3[𝑒𝑠𝑝𝑖𝑟𝑎𝑠] 8 ∗ (8 ∗ 0,5) ∗ 131,24 Hallamos la longitud solida: 𝐿 = 𝑑(𝑁 + 1) = 5(3 + 1) = 2[𝑐𝑚] Hallamos el paso: 𝑝= (𝑏 − 𝑑) (3 − 0,5) = = 0,83[𝑐𝑚] 𝑁 3 Hallamos la longitud libre: 𝐿 = 𝑝𝑁 + 𝑑 = (3 ∗ 0,83) + 0,5 = 3 [𝑐𝑚]