
• •
•O
Matemática
• •
• • Vectores
Silvia V. Altman | Claudia R .Comparatore | Liliana E. Kurzrok
M A T EM Á TIC A | LIB R O 4
Vectores
Dirección editorial
Supervisión gráfica
Las autoras agradecen a
Verónica Parada
Gabriela Feidman
la profesora Patricia Sadovsky
Dirección pedagógica
Diseño gráfico
Natalia Fernandez
apoyo incondicional.
Rosa Rottemberg
por sus enseñanzas y su
Corrección
Inés Gugüoteila
Dirección de arte
Paula Lanzillotti
Diseño de signos
tipográficos matemáticos
Natalia Fernández
Edición
Nora Legorburu
Ilustración de
tapa e interiores
Doma
Gráficos
Natalia Fernández
Fotografía
Archivo Longseller
El Correo de la UNESCO
Fotocromía
Longseller S.A.
® EDITORIAL LONGSELLER SJK.
Libro d e edición arg e n tin a.
Casa m atriz: Av. San Ju an 777
Está prohibida y pe n ad a por la le y la re­
514-7
ALT
(C1147AAF)
producción to ta l o parcial de e s t e libro,
A ltm an , Silvia
M a te m ática 4 : ve cto re s / Silvia A ltm a n ,C laudia
C om p arato re y Liliana K urzrok.-i a ed.- B u e n o s A îres:
Ciudad de B u e n o s Aires, A rg en tin a
en c u alq u ie r fo rm a, por m e d io s m e cá­
T eléfono y fa x : (5411) 5 0 3 1- 5 4 0 0
nicos, electrón icos, in fo rm áticos, m ag ­
E -m a il:e d u ca c¡on @ lo n g seller.co m .ar
n éticos, in clu so fo to c o p ia y c u alq u ie r
w w w .lo n g se lle r.co m .ar
otro siste m a d e a lm a c e n a m ie n to de
ISBN Obra C o m p le ta: 9 8 7 -9 4 8 1-6 6 -6
in fo rm ación . C u alq u ier reproducción
Longseller, 2 0 0 1.
112 p.; 28 x20cm .-(L ¡b ros te m átic o s)
ISBN 9 8 7 -5 5 0 -0 4 1-0
1. C om paratore, C lau d ia II. Kurzok, Liliana III.T ítu lo 1. V ectores
O u ed a hech o el d e p ó sito q u e d ispo n e
sin el previo co n se n tim ien to e sc rito del
la ley 11.723.
e d ito r viola los d e re ch o s re servad o s, e s
Libro de ed ición arg e n tin a.
ilegal y c o n stitu ye un delito.
§
• •
§
• ©
I
•
°
<3
.<
flj
Matemática
•
• • Vectores
Silvia V.AItman
Profesora de Matemática y Astronomía, INSP "Joaquín V. González”.
0
Ganadora del Subsidio para profesores de colegios secundarios, Fundación Antorchas (1994).
Docente en escuelas medias.
Claudia R. Comparatore
Licenciada en Matemática, Universidad Nacional de Buenos Aires.
Ganadora del Subsidio para profesores de colegios secundarios, Fundación Antorchas (1994).
Docente en escuelas medias y en la Facultad de Ciencias Exactas, UBA.
Liliana E. Kurzrok
Licenciada en Matemática, Universidad Nacional de Buenos Aires.
Profesora de Matemática, ORT Formación docente para profesionales.
Beca ria de Investigación, CONICET, UBA.
Docente en escuelas medias y en la Facultad de Ciencias Exactas, UBA.
M A T EM Á TIC A | LIB R O 4
6
Vectores
Cómo leer este libro
■
| Problemas
Posible resolución
Al comenzar cada capítulo,y
para introducir los contenidos,
Se presenta un posible camino
para resolver cada uno de los
se presentan uno o más pro­
problemas propuestos, que per­
blemas para resolvery discutir
en grupos, que se identifican
mite confrontar diferentes pro­
cedimientos y verificar las solu­
con el icono O .
ciones obtenidas. Se identifica
Algo más...
Se presentan comentariosy
aclaraciones sobre los temas
desarrollados.
con el icono # .
Lean atentamente las consignas.Inter­
cambien Ideas entre los Integrantesdel
grupo. 51Intentan resciverel problema a
partir de loque propuso unode ustedes)
alternativas para determinar si siguen
pensando que los motivos pof loscuales
fueron dejadasde ladoson válidos.
Un grupo de ingenieros está construyendo un robot que será
manejado poruña computadora. Se proponen diseñar un pro­
grama para coma ndar sus moví mlentos con la menor cantidad
de datos posibles. ¿Cuáles son los datos que deberían Introdu­
cir en la máquina?
Para Interpretar mejor el problema, representemos la situación
en un esquema. Supongamos que el robot está ubicadoen el
punto A y queremos que se traslade hasta el punto B,queestá
a 2 m deA
que la definen. Por ejemplo,si quere­
mos trasladarel rectánguloABCDse­
gún un vector vi debemoshallarías
Imágenes de sus cuatrovértices. Para
elk), trazamos a partir deA,B,CyDsegmentos paralelos a v,y construimos un
vector con Igual serrtidoy móduloque
El matemático que Introdujo la palabra
vector fue W1Illam Rowan Hamltton.Naci­
do en Dublln, Irlanda, en 1805,a los anco
afiosya estudiaba latín, grfegoy hebreo
estudiar Matemática y a losqulnce, los
trabajos de Newton y Laplace. Cuandote­
nia dieciocho artos. Ingresé en el THnlty
College, en Dublln, y obtuvo unadistin­
ción que sólose da una vez cada veinte
afios. En 1827,fue nombradoprofesorde
Astronomía enel TrlnltyColle^pnrseto—
veintiún añosy sin haberse recibido, lo
cual motivólas criticas deotrosprofeso­
res, que pensaban que noteniasuficiente
experiencia en hacer observaciones. Al
añosiguiente, se lo nombróastrónomo
real para Irlanda. DesarrollótamWin nu­
merosos trabajos enópticay dinámica.
Fallecióen Irianda,en1B65.
Una traslación devectortes
din que atodo punto P del pl¡ ni
asigna otro punto P"del plano, demodo
que el vector Retiene la ml^llrecdón, sentidoy módulo que t,
Cuando queremos trasladar una figura,
basta con hallar la Imagen,a travésde
O Problema 2
Una vez que el robot está terminal
En primer lugar, le dan instrucción
desde el escritorio hasta la blbltote
desde allí hasta la puerta.Si qulsie
ra directamente desde el escritorio
movimiento quede ben Indicarle? {
>,comienzan a probarlo.
¡ para que se traslade
a; Iuego, para que vaya
m que el robotse desplazalasta la puerta, ¿cuál es el
eñálenlo en el dibujo.)
El robot debe:
1) Moverse sobre la recta determinada porA y 0.
2) Partirde A en dirección a B.
3) Avanzardos metros.
Vemos que, para lograr que el robot alcance el objetivo pro­
puesto, debemos darle tres referencias.
{Cómoi« lm_?
L Dirección: Está definida pof la recta determinada por
los puntosAyB. Se considera que los movimientos sobre
rectas paralelas tienen la misma dirección.
2. Sentido: En cada dirección, hay dos sentidos (en nuestro
ejempío, puede ser deA a B o de B aA).
3. Módulo; Es la longitud del segmento determinado por
las posiciones inicial y final del movimiento.
^tora
1. En cada caso, dibujen unvector
porelcualse puedetrasladarF,ala
posldón F,.
Por lo tanto, el desplazamiento del robot queda identificado
mediante un segmento orientado; en nuestroejemplo: AB.
Se llama wctorAB al segmento orientado que
Ayterm!nae(^
Simbólicament , se escribe Al
Al puntoAsel«le llama origtnyal B,
Cómo se lee...?
Se ofrece el significado de los
símbolos utilizados en la página.
Textos recuadrados
Actividades
Se presentan biografías, reseñas
Aquí se incluyen definiciones
Se proponen actividades que
históricas y datos de interés, que
enriquecen los contenidos.
para que puedan ser localizadas
sirven para verificar la compren­
rápidamente cuando se necesi­
sión de los contenidos abordados
y la aplicación de éstos en distin­
ta consultarlas.
tas situaciones.
7
Guía de ejercitación
Guía de autoevaluación
Incluye actividades orientadas
a poner enjuego todos los con­
Contiene actividades que pue­
den ser resueltas alfinalizar el
ceptosy procedimientos desarro­
capítulo para autoevaluar lo
llados a lo largo del capítulo.
aprendido.
Se incluyen las respuestas alfinal
del libro.
CE 3
MATFMÁTIr"A 11IRRfl 4
Vectores
Geometría analítica
GUÍA DE EJERCITACIÓN
16. Encuentren la Intersección entre los siguientes planos:
a.TT:2x-y+z-Q
TT': 3x +2 y - z - 5
H
l| fj
aBjS
O
P|
®
Bra
CA 3
GUÍA DE AUTOEVALUACIÓN
I
1
1
MATPMAT.CAl.mtn4
Vectores
Coometría anaftka
1. Completar, si es posible, las coordenadas de los puntos para que pertenezcan a la recta o
al plano indicada.
O
a. (2;___ ) en la recta L X - k (-1; 2) + (3¡ 4),con kc R
b.TT:x+3y-2z=4
TT: 3x +9y-6z =10
t (1; 2;___ ) en la recta UX = k (2; 4;-8), con k c R
O
O
« - f t— 5-1)en la recta ü |3 y - x =4
t ( - l ¡ — ; — )enlar<
17. Encuentren la intersección entre la recta Ly el plano IT, donde;
L:X =k (-5; 4; 1) + (-1; 1; O) kcR
TT:3x-4y= -69
O
f.(2;-6;___ Jen el planoTT:2x-7y+4z =10
O
2. Determinar la ecuación de la recta que pasa por el puntode intersección entre Ly L’,y es
paralelas la recta que pasa por los puntos (2; l)y {-3 ; 4), donde;
18. Determinen si la recta Lestá contenida en el planoTT,donde:
b ^ ^ -y-z-1
L X = k{2; 2) + (1; —
1) kER
TT:y+z-3
O
o
3. Encontrar una dirección para cada una de las siguientes rectasdel espacto. Escribir su
ecuaciónvectorialyhallartres puntos que pertenezca n a cada recta,
a. L- [y - 3x - 6
12x - 3z ■-6
19. Determinen si la recta Lestá contenida en el píanoTT,donde:
Lx-2 -y+ 4 -z-1
TT:-y+z- 5
O
O
i
79
M A T EM Á TIC A | LIB R O 4
8
Vectores
índice
• • • 6 • • • • • • • •
• • • • •
'* •
•
>
• • •<9 « > • • • •
• • • • « » ••••
< & ••••
''V
K
T
ir
t
i
J
iü
• ó
11
Capítulo i
18
Vectores en el plano
19 Coordenadas cartesianas
12 Problemas y resoluciones
13 Vector
14 Vectores paralelos
Vectores equivalentes
20
Problemas y resoluciones
35
Capítulo 2
de un vector
36
Problemas y resoluciones
Coordenadas polares de un vector
39
Coordenadas cartesianas de un vector
21
Problemas y resoluciones
Combinación lineal de vectores
40
Problemas y resoluciones
42
en el espacio
Problemas y resoluciones
Operaciones con vectores en el espacio
15 Problemas y resoluciones
Operaciones con vectores enforma
Suma
16 Suma de vectores
cartesiana
Resta
Vectores paralelos en coordenadas
Multiplicación por un escalar
cartesianas
Producto escalar
Resta de vectores
23
17 Problemas y resoluciones
Producto de un vector por un escalar
Producto escalar de vectores
44
(número real)
Propiedades del producto escalar
45 Ángulo entre dos vectores
24
25
<é1- ■»
Vectores en el espacio
22
Vectores opuestos
va« • • • • •
Problemas y resoluciones
Producto escalar de dos vectores da­
Vectores ortogonales
dos por sus coordenadas cartesianas
Producto vectorial
Vectores ortogonales
Problemas y resoluciones
26 Ángulo entre dos vectores
27 Guía de ejercitación
33 Guía de autoevaluación
9
46 Propiedades del producto vectorial
67 Planos en el espacio
47 Problemas y resoluciones
68 Planos coordenados
81 Capítulo 4
Cónicas
49 Guía de ejercitación
Representación gráfica de un plano
82 Problemas y resoluciones
55 Guía de autoevaluación
en el espacio
83 Lugar geométrico
69 Problemasyresoluciones
57 Capítulo 3
Geometría analítica
58 Problemas y resoluciones
60 Ecuación vectorial de la recta que
pasa por el origen y tiene dirección v
Problemas y resoluciones
61 Distintasformas de la ecuación de
7° Plano que pasa por tres puntos
71 Paralelismo y perpendicularidad en­
tre rectas y planos
73 Guía de ejercitación
79 Guía de autoevaluación
Circunferencia
84 Problemas y resoluciones
87 Elipse
88 Problemas y resoluciones
95 Hipérbola
97 Problemas y resoluciones
99 Parábola
100 Secciones cónicas
la recta que pasa por dos puntos
Problemas y resoluciones
62 Rectas en el espacio
101
63 Problemas y resoluciones
107 Guía de autoevaluación
64 Rectas paralelas
109
65 Rectas perpendiculares
Problemas y resoluciones
66 Rectas alabeadas
Problemas y resoluciones
Guía de ejercitación
Respuestas
M A T E M Á T IC A | LIB R O 4
Vectores
1 Vectores en el plano
Hay diversas situaciones en las cuales un
número no alcanza para describirlas.
Por ejemplo, cuando en Física se debe identificar
unafuerza, se necesita indicar de cuánto esy
hacia dónde va. En este capítulo, veremos
cómo se define matemáticamente este tipo de
información.
M A T E M A T IC A I L IB R O 4
12
VECTORES EN EL PLANO
Lean atentamente las consignas. Inter­
Vectores
O Problema 1
cambien ideas entre los integrantes del
grupo. Si intentan resolver el problema a
partir de lo que propuso uno de ustedes y
Un grupo de ingenieros está construyendo un robot que será
no lo logran, vuelvan a analizar las otras
grama para comandar sus movimientos con la menor cantidad
alternativas para determinar si siguen
de datos posibles. ¿Cuáles son los datos que deberían introdu-
pensando que los motivos por los cuales
fueron dejadas de lado son válidos.
manejado por una computadora. Se proponen diseñar un pro­
ciren la máquina?
¿Sabían que...?
El matemático que introdujo la palabra
vector fue William Rowan Hamilton. Naci­
do en Dublín, Irlanda, en 1805, a los cinco
años ya estudiaba latín, griego y hebreo
con un tío. A los trece años, comenzó a
estudiar Matemática y a los quince, los
trabajos de Newton y La place. Cuando te­
nía dieciocho años, ingresó en el Trinity
College, en Dublín, y obtuvo una distin­
ción que sólo se da una vez cada veinte
años. En 1827, fue nombrado profesor de
Astronomía en el Trinity College con solo
veintiún años y sin haberse recibido, lo
cual motivó las críticas de otros profeso­
res, que pensaban que no tenía suficiente
experiencia en hacer observaciones. Al
año siguiente, se lo nombró astrónomo
O Problema 2
Una vez que el robot está terminado, comienzan a probarlo.
En primer lugar, le dan instrucciones para que se traslade
real para Irlanda. Desarrolló también nu­
merosos trabajos en óptica y dinámica.
desde el escritorio hasta la biblioteca; luego, para que vaya
Falleció en Irlanda, en 1865.
ra directamente desde el escritorio hasta la puerta, ¿cuál es el
desde allí hasta la puerta. Si quisieran que el robot se desplaza­
movimiento que deben indicarle? (Señálenlo en el dibujo.)
• Problema 1
Algo más...
Para interpretar mejor el problema, representemos la situación
en un esquema. Supongamos que el robot está ubicado en el
punto A y queremos que se traslade hasta el punto B, que está
a 2 m de A.
Una traslación de vector te s una fun­
ción que a todo punto P del plano le
asigna otro punto P’ del plano, de modo
que el vector PP’ tiene la misma direc­
ción, sentido y módulo que t.
Cuando queremos trasladar una figura,
xB
basta con hallar la imagen, a través de
la traslación de vector t, de los puntos
que la definen. Por ejemplo, si quere­
mos trasladar el rectángulo ABCD se­
gún un vector v, debemos hallar las
imágenes de sus cuatro vértices. Para
ello, trazamos a partir de A, B, C y D seg­
xA
mentos paralelos a v, y construimos un
vector con igual sentidoy módulo que
este vector.
A
El robot debe:
D
1) Moverse sobre la recta determinada por A y B.
2) Partir de A en dirección a B.
3) Avanzar dos metros.
Vemos que, para lograr que el robot alcance el objetivo pro­
\
\
V\
\
\
A’
D’
B
C
\
\
puesto, debemos darle tres referencias.
Vector
En matemática, a cada uno de estos datos se le asigna un
nombre diferente:
1. En cada caso, dibujen un vector
por el cual se puede trasladar F1a la
posición F2.
1. Dirección: Está definida por la recta determinada por
los puntos A y B. Se considera que los movimientos sobre
rectas paralelas tienen la misma dirección.
2. Sentido: En cada dirección, hay dos sentidos (en nuestro
ejemplo, puede ser de A a B o de B a A).
3. Módulo: Es la longitud del segmento determinado por
las posiciones inicial y final del movimiento.
Por lo tanto, el desplazamiento del robot queda identificado
mediante un segmento orientado; en nuestro ejemplo: AB.
Se llama vector AB al segmento orientado que empieza en
A y termina en B.
Simbólicamente, se escribe AB.
Al punto A se lo llama origen y al B, extremo.
M A T E M A T IC A I L IB R O 4
14
Vectores
VECTORES EN EL PLANO
2. Dibujen un vector equivalente a AB:
En el problema, queremos que el robot se traslade según el
vector AB.
Por lo tanto, en la computadora se debe introducir como
dato un vector, es decir, deben darse la dirección, el sentido
y el módulo.
3. Dibujen un vector opuesto a CD:
Vectores paralelos
Dos vectores son paralelos si tienen la misma dirección.
Por ejemplo, los vectores MN, O PySRson paralelos.
N
S
M
4. Dibujen un vector paralelo a MN, que
Q
no sea equivalente a él.
R
Vectores equivalentes
Dos vectores son equivalentes si son paralelos, tienen el
mismo sentidoy el mismo módulo.
Por ejemplo, los vectores MN y PO son equivalentes.
Vectores opuestos
Dos vectores son opuestos si son paralelos, tienen igual
módulo y sentido opuesto.
Por ejemplo, los vectores MN y OP son opuestos. Se indica que
MN = - O P .
M
P
• Problema 2
Recordemos el movimiento que tiene que hacer el robot por
5. Hallen el vector suma en cada uno de
los siguientes casos:
medio de un esquema, y representemos en él cada uno de los
desplazamientos, a través de un vector:
Escritorio (E)
El robot se desplazó, en primer lugar, según el EB y luego, se­
gún el BP, y llegó al mismo lugar que si se hubiese trasladado
según el EP.
A este nuevo vector lo llamaremos vector suma de los otros dos.
Simbólicamente:
ÉB + BP = ÉP.
Observen que el vector suma tiene su origen en el origen del
primer vector y su extremo, en el extremo del segundo.
En este caso, el extremo del primer vector coincide con el ori­
gen del segundo. Si los vectores que tenemos que sumar no
cumplen con esta condición, tomamos dos vectores equivalen­
tes a los dados que cumplan con ella.
a.
16
VECTORES EN EL PLANO
6. Consideren los siguientes vectores:
Vectores
Suma de vectores
Para sumar dos vectores, se toman, si es necesario, dos
A
vectores equivalentes a los dados, que cumplan con la
condición de que el extremo del primero coincida con el
origen del segundo. La suma de estos vectores es otro
vector que tiene su origen en el origen del primero y su
extremo, en el extremo del segundo.
F
i
c
Si consideramos dos vectores que tienen el mismo origen, al
realizar la suma queda:
Crafiquen:
a .Á B -ÍH
b.CD-EF
c .É F - ÍH
Vemos que el vector suma es la diagonal del paralelogramo, en
el cual dos de sus lados son v y w . Este método para sumar se
conoce como regla del paralelogramo.
Resta de vectores
Para restar dos vectores, se suma al primero el opuesto
del segundo: Á B - CD =ÁB + (-CD)
Por ejemplo, si queremos restar los vectores A B y CD:
17
¿Sabían que...?
O Problema 3
Maurits Cornelis Escher nació en 1898,
Observen esta obra de Escher, en la que aparece una figura
repetida varias veces. Indiquen qué movimientos permiten
pasar de la figura
a- 1 a la 2
b. 2 a la 3
:
c í a la 3
adolescencia no fue un buen estudiante:
repitió dos veces un curso y no obtuvo el
título final. Como su padre quería que re­
/ } r
cibiera una formación científica impor­
c
-JJ
en Leeuwarden (Países Bajos). Durante su
tante para llegara ser arquitecto, en 1919
Escher comenzó a estudiar en la Escuela
de Arquitectura y Artes Decorativas de
Haarlem. En esta escuela, enseñaba artes
gráficas Samuel Jesserun de Mesquita,
quien comprobó el talento de este mu­
chacho y convenció al padre para que lo
dejara cambiar la arquitectura por el arte
decorativo. Con él, Escher aprendió la téc­
O Problema 3
nica del grabado en madera. En 1922, viajó
Podemos ver, en el dibujo, que para pasar de la figura 1 a la 2,
se aplica el mismo vector que para pasar de la figura 2 a la 3;
a Italia, donde vivió hasta 1935, año en
que se mudó a Suiza por no estar de
acuerdo con el régimen de Mussolini.
entonces, el vector de traslación de la figura 1 a la 3 es dos
Luego volvió a Holanda, en 1941. Allí falle­
veces dicho vector.
ció el 27 de marzo de 1972.
Podemos escribir: 2 . AB = AC
Dentro de su obra, se encuentran estam­
pas del paisaje del sur de Italia y del Medi-
Producto de un vector
por un escalar (número real)
terráneo,y alrededor de setenta trabajos
de inspiración matemática. Su interés por
las figuras matemáticas tiene su origen
en la admiración que le causaban los
El producto de un vector v por un escalar (número real)
positivo es un vector que tiene igual dirección y sentido
que v, y cuyo módulo es el producto del módulo de v por
cristales. Después de un intenso estudio,
inventó un método para partir regular­
mente la superficie plana. A partir de una
figura geométrica que cubría el plano,
el número real dado.
efectuaba particiones para obtener nue­
vas figuras, como podemos ver en la que
Por ejemplo, para hallar 3 . AB, procedemos así:
presentamos en el problema 3. Escribió un
tratado sobre este tema y otro sobre la
aproximación al infinito.
t-----
h
B
El producto de un vector v por un escalar negativo es un
vector que tiene igual dirección que v, sentido opuesto y
cuyo módulo es el producto del módulo de v por el valor
absoluto del número real dado.
Por ejemplo, para h allar-3 . AB = 3 . (-AB), hacemos:
M A T E M A T IC A I L IB R O 4
18
Vectores
VECTORES EN EL PLANO
7. Dados los puntos A, B y C, hallen
O Problema 4
gráficamente:
Volvamos a los ingenieros que construyen el robot. ¿Cómo se
a. 2 ÀB
le puede indicar a la computadora cuál es la dirección, el senti­
do y el módulo del vector que define cada movimiento?
b . - l BC
c.
\
2
• Problema 4
AC
Hasta aquí hemos analizado los vectores, pero, para determi­
nar los desplazamientos, podemos descomponerlos en dos
movimientos a partir de la posición inicial: uno vertical y otro
horizontal.
Ax
Por ejemplo, una traslación puede ser 1 m a la derecha hori­
zontalmente y 2 m hacia arriba verticalmente. De esta manera,
xB
la información que introducimos en la computadora es un par
de números (1; 2), que está definiendo el movimiento.
Cx
Si graficamos el vector en un sistema de ejes perpendiculares,
con centro en la posición inicial (A):
vemos que las coordenadas de la posición final B del robot son
(1; 2). Es decir que cuando el origen del vector coincide con el
origen de coordenadas, el vector queda identificado con las
coordenadas del extremo.
Si consideramos, ahora, un vector cuyo origen sea un punto
distinto de A, podemos encontrar siempre un vector equivalen­
te, con extremo en el origen de coordenadas.
19
Coordenadas cartesianas de un vector
Veamos cómo podemos hallar las coordenadas cartesianas de
un vector AB, conociendo las coordenadas del origen y el extre­
mo de dicho vector:
Si sabemos que A = (3; 5) y B = (8; 7), tenemos que hallar las
coordenadas de O y de P para que el vector OP sea equivalente
con AB. Vemos que los triángulos AMB y OOP deben ser con­
gruentes, por ser rectángulos y tener congruentes la hipotenu­
sa y el ángulo que ésta forma con la horizontal; por lo tanto,
tenemos que averiguar la longitud de los segmentos AM y
BM para que O O yPO tengan, respectivamente, las mismas
longitudes.
Calculemos la longitud de AM.
Sabemos que desde el eje de ordenadas hasta A hay 3 unida­
des, y hasta M hay 8 unidades; entonces, |AM| = 8 - 3 = 5.
Análogamente,| BM| = 7 - 5 = 2. Por lo tanto, P = (5; 2) y
OP = ÁB = (5; 2).
Las coordenadas cartesianas de un vector son las coorde­
nadas del extremo de un vector equivalente al mismo,
cuyo origen es el origen de coordenadas.
Si A = (a; b) y P = (p; q) son las coordenadas cartesianas
de los extremos de AP, entonces las coordenadas cartesia­
nas de AP son (p - a; q - b).
Por lo tanto, en el plano cartesiano, cada vector queda identifi­
cado con un punto, pues cada punto está definido por un par
ordenado de la forma (x;y); entonces, este par ordenado tam ­
bién determina un vector con origen en (0; 0).
8. Escríban las coordenadas cartesianas
de los siguientes vectores:
i iOt
!
20
VECTORES EN EL PLANO
9. Dibujen todos los vectores con
origen en (0; 0):
Vectores
Se llama IR2 al conjunto de todos los pares ordenados de la
forma (x; y), donde x e y son números reales.
a. cuyo módulo es 3
Coordenadas polares de un vector
A
Otra forma de definir el desplazamiento es considerando el
ángulo que el vector forma con la horizontal y su longitud.
De esta manera, el vector queda definido por este ángulo y
su módulo. A esta forma de definir un vector se la llama
coordenadas polares.
------------------------------------- ►
Podemos ver que se pueden considerar ángulos diferentes
para un mismo vector.
b. cuyo argumento está entre 60°y 120°
4
Se llama argumento de un vector al único ángulo entre 0°
y 360° que determina el vector con el semieje positivo de
las abscisas.
Por ejemplo, el vector AB tiene módulo 3yfo rm a con la hori­
zontal un ángulo de 50°.
Las coordenadas polares de un vector están dadas por el móduloy el argumento de dicho vector.
¿Cómo hallamos las coordenadas polares de un vector, cono­
ciendo sus coordenadas cartesianas?
Sea v el vector de coordenadas (x^ y j :
O
21
Para hallar el módulo del vector, basta con aplicar el Teorema
de Pitágoras en el triángulo rectángulo OAP:
10. Escriban las coordenadas polares de
cada uno de los siguientes vectores:
|v |= V x 7 + y 7
Para hallar el argumento de V , consideramos tg c|> =
T=(5; 3) =
Por ejemplo, si v = (-1; -3)
b = (0; 4) =
su módulo es: | v| = V i 2+ 32= VÍO.
Para hallar <|>: tg <|> = — = 3.
Si utilizamos la calculadora para hallar el ángulo, obtenemos
71° 33’ 54”; sin embargo, el argumento de este vector está en
el tercer cuadrante. Luego, 71° 33’ 54” es un ángulo del trián­
gulo OAP, por lo tanto:
= 71° 33’ 54” + 180° = 251° 33’ 54”.
O Problema 5
Observen los vectores a y b. Escriban al vector c como el resul­
tado de operaciones que combinen a, b y números reales.
Representemos en un esquema los tres vectores, a partir de un
mismo punto.
Podemos ver que c = 3 a - 2 b. Cuando un vector puede ser
escrito como suma o resta de otros, se dice que es una
combinación lineal de ellos.
c = (7; 2) =
22
VECTORES EN EL PLANO
11. Dados los vectores a = (7; 3),
Vectores
Combinación lineal de vectores
b = ( l ; 5) y ~C= (15; 11):
Un vector a es combinación lineal de otros vectores v1( v2, v3
a. Hallen un vector que sea
combinación lineal de a y b.
si existen números reales
a2; a3; ... tales que
a = Sj Vj + a2v2+ ... .
¿Es único? ¿Porqué?
O Problema 6
Sean a = (2; 4) y b = (-3; -2), hallen las coordenadas de los
vectores: a + b; 3 a y -2 b.
b. Hallen un vector que sea
combinación lineal de c y b.
¿Es único? ¿Porqué?
• Problema 6
Si representamos en un esquema cartesiano los vectores a y b,
c. Hallen un vector que sea
combinación lineal de a, b y c.
¿Es único? ¿Porqué?
Vemos que el vector a + b tiene como primera coordenada la
suma de las primeras coordenadas de a y de b ,y como segun­
da coordenada, la suma de las segundas coordenadas de a y
de b. Las coordenadas del vector 3a son el triple de las de a, y
el vector -2b tiene las coordenadas de b multiplicadas por -2.
Operaciones con vectores en forma cartesiana
La suma de dos vectores, definidos en forma cartesiana, es
otro vector cuyas coordenadas son la suma de sus respec­
tivas coordenadas.
Siendo a = (a^ a2) y b = (b^ b2) => a + b =
+ b^ a2+ b2)
El producto de un vector, definido en forma cartesiana,
por un escalar es otro vector cuyas coordenadas son las
coordenadas del vector multiplicadas por dicho escalar.
Por ejemplo, (2; -7) + (0; -1) = (2; -8); 3 (-8; 6) = (-24; 18).
23
Vectores paralelos en coordenadas cartesianas
Si los vectores a y b son paralelos, cuando tomamos vectores
equivalentes que pasan por el origen de coordenadas, éstos
12. Dados los vectores a = (7; -3),
b = (-1; 6) y c = (-4; -3), hallen:
a + b = _____________________________
están sobre la misma recta; por lo tanto, tienen la misma incli­
c + a = ___
nación y | a | = k . | b|, con k e IR.
a + b +c =
Con lo cual, si a = (ax; a ) y b = (bx; b ), entonces:
b - a =____
2a = ______
ax = | a| eos <|>;ay = | a| sen 4>
b„= fb| eos <|); b = |”b|sen <|j
3c-4 a =
pero | a| = k . | b|, con k e IR; entonces,
ax = | a| eos 4>= k . | b| eos
ay = | a| sen
= k . bx
= k . | b| sen <|>= k . by
'(ax; a ) = k . (bx; b
Conclusión
Si dos vectores a y b son paralelos, a = k . b, con k e IR.
Producto escalar de vectores
El producto escalar de dos vectores a y b es el número
| a| | b| eos a , siendo a el ángulo determinado por dichos
vectores. Se simboliza:
a . b = | a| | b| eos a
Como | a|, | b| y eos a son números reales, entonces el pro­
ducto escalar entre dos vectores da por resultado un número
real y no un vector.
Por ejemplo, si los vectores a y b determinan un ángulo de 60°,
| a| = 2 y | b| = 4; entonces,
a . b = | a| | b| eos a = 2 . 4 . 0 , 5 = 4
Propiedades del producto escalar
Sean a y b dos vectores y n e IR:
1. Propiedad conmutativa: a . b = b . a
2. Propiedad distributiva respecto de la suma de vectores:
a.(b + c)= a.b + a.c
3. n . (a . b) = (n . a ) . b
13. Escriban las coordenadas de tres
vectores paralelos a v = (5; 2):
M A T E M A T IC A I L IB R O 4
24
VECTORES EN EL PLANO
Vectores
14. Analicen la demostración de la pro­
4. Si dos vectores tienen la misma dirección, el producto
piedad del producto escalar de dos vec­
tores que tienen la misma dirección.
escalar de ambos es 1 ó - l por el producto de los módulos,
según tengan igual o distinto sentido:
Utilícenla como referente y demuestren
las otras propiedades del producto esca­
lar que se enuncian en esta página y en
a .b = |a||b|
ó a . b = |a||b|
la anterior.
Para demostrar esta propiedad, basta con considerar la defini­
ción del producto escalar: a . b = | a| | b| eos a , y que si dos
vectores tienen la misma dirección, determinan un ángulo de
0° o de 180°.
En el primer caso, eos 0° = 1, y en el segundo, eos 180° = -1.
Entonces:
a . b = | a | | b | . l = | a | | b | ó a . b = | a | | b | (-1) = —| a | | b |.
5. El producto escalar de un vector por sí mismo es el cuadrado
de su módulo:
a . a = | a |2
6. Si dos vectores son perpendiculares, su producto escalar es 0.
Producto escalar de dos vectores dados
por sus coordenadas cartesianas
Consideremos los vectores a y b, cuyas coordenadas son (a^ a2
y (bj; b2), respectivamente.
Entonces:
a y b pueden escribirse como combinación lineal de
v = (1; 0) y w = (0; 1), de la siguiente manera:
b = bj v + b2w
Entonces: a . b = ^ v + a2w ) . (bxv + b2w).
Aplicamos las propiedades distributiva y asociativa (teniendo
en cuenta que a1( a2, bx, b2e IR):
a . b = a1. b 1. ( v . ~v) + a 1. b2. ( v . w) + b2. ax. ( w .
+ a2. b2. ( w . w)
Como v y w son perpendiculares: v . w = w . v = 0
y,adem ás, v . v = | v |2= 1 y w . w = | w | 2 = l
+
25
Conclusión
Algo más...
El producto escalar de dos vectores dados en coordenadas
El producto escalar de vectores resulta
una herramienta útil para la Física, pues
cartesianas es: (a^ a2) . (bx; b2) = a 1. bx+ a2. b2
se puede calcular el trabajo de una fuer­
za como el producto escalar entre dicha
fuerza y el desplazamiento del cuerpo
Por ejemplo, el producto escalar entre los vectores
sobre el que está aplicada dicha fuerza.
"a = (-2,3 ) y "b = (-5; 8) es
Por ejemplo, si tenemos un autito:
"a. “b = (-2 ). (-5)+ 3 .8 = 34
Vectores ortogonales
Dos vectores a y b son ortogonales o perpendiculares
si a . b = 0.
Cuando le aplicamos la fuerza f, se pro­
Simbólicamente, a l b.
duce un desplazamiento D. (En Física, se
Por ejemplo, los vectores v = (1; 0) y w = (0; 1) son ortogonales
lo suele escribir A x por ser la variación
de posición.)
pues (1; 0 ). (0; 1) = 1 . 0 + 0 .1 = 0.
Si llamamos a al ángulo determinado
por ambos vectores, el trabajo realizado
O
p o r f e s L f = |f | | D | c o s a .
Cuando el ángulo a es menor que 90°,
se favorece el desplazamiento; cuando
1-
es mayor que 90°, el desplazamiento
se dificulta, y cuando es de 90°, no hay
V
trabajo porque no hay componente
de la fuerza en el sentido del desplaza­
W'
w
1
©
miento.
El producto escalartambién se utiliza
en Física para calcular el flujo en un
campo eléctrico o magnético.
Los vectores (1; 0) y (0; 1) se llaman versores elementales.
O Problema 7
Hallen el ángulo a , 0° < a < 180°, que forman los vectores a y
b, cuyas coordenadas cartesianas son (5; 4) y (-2; 6), respecti­
vamente.
©t
©
M A T E M A T IC A I L IB R O 4
26
VECTORES EN EL PLANO
15. Dados los vectores a = (7; -3),
b = (-1; 6) y c = (-4; -3), calculen:
l í . ~6=_______________________
a. c=
(la + Ti ). "c = .
Vectores
• Problema 7
Calculemos el producto escalar de los vectores mediante las
dos formas que conocemos para hacerlo:
"a ."b = (5; 4 ). (-2; 6) = 5 . (-2) + 4 .6 = 14 (i)
a . b = | a| | b| eos a
(2)
a.(í-"c) =.
Hallemos los módulos de a y de b:
16. Hallen los ángulos determinados
por los vectores a y b, y por a y c del
ejercicio anterior.
|"a| = V52+ 42= V41
|"b| = V(-2)2+ 62= a/40 = 2VlO
De (i) y (2)
14 = V 4 Í . 2 V l0 . eos a ; entonces,
eos a =
17. Dado el vector v = (5; 3):
14
2V Í0 V41
14
40,5
0,3457 => a = 69° 46’ 30”
Ángulo entre dos vectores
a. Propongan las coordenadas de un
vector que forme un ángulo de 50° con
v. ¿Es único?
El ángulo a , 0° < a < 180°, que forman los vectores a y b
cumple que:
eos a =
a. b
a| | b|
0° < a < 180°
Observen que estamos considerando el ángulo ex entre 0 °y
b. Propongan las coordenadas de un
vector perpendicular a v.
180°, para que sea el menor de los ángulos que determinan
los vectores. De este modo, hay unicidad en la elección del
ángulo, ya que entre 0 °y 180° la función coseno es inyectiva.
GE 1
GUIA DE EJERCITACION
Vectores
Vectores en el plano
1. Dados los vectores AB, CD y DE, hallen:
a. ÁB+ CD
b. B. ÁB
c. ÁB - 2 . DE
d . 2 . ( Á B + DE)
2. Sabiendo que OA = a, OB = b, AP = 20A , BO = OB y PN = NO, expresen los siguientes
vectores en función de a y b:
a. OP
b.ÓN
c. PN
d.OP
3. Sabiendo que OA = a, OB = b, AO = ^ a. BR = b y AP = 2 BA, expresen los
siguientes vectores en función de a y b:
a. BA
b. BP
c. RO
d. OA
GE 1
GUIA DE EJERCITACION
I
Vectores
£
Vectores en el plano
4. Escriban las coordenadas cartesianas de cada uno de los siguientes vectores:
O
5. Hallen los valores de m para que los siguientes vectores tengan el módulo dado:
a. v = (m -1 ; 3)
|v | =5
b. v = (-2; m)
I vi =4
o
6. Escriban en coordenadas polares los vectores del ejercicio 4.
O
7. Escriban en coordenadas cartesianas los siguientes vectores dados en forma polar:
O
a. | v| = 5, <|>= 30°
b. | v| = 2, <j) = 80°
O
c. | v| = 1 0 ,4>= 180°
ALU M N O
CURSO
FECH A
GE 1
GUÍA DE EJERCITACIÓN
8. Hallen la resultante (suma) de los pares de fuerzas siguientes:
O
O
9. Escriban los siguientes vectores como combinación lineal de v = (5; 3) y w = (8; 4):
a. 7= (3; 2)
b .d = (9;7)
c. e = (0; 2)
d. f= (- 2 ; 0)
o
o
10. Dados los puntos M = (1; 3), N = (3; 7), P = (5; 1) y O = (2; 6), determinen, sin represen­
tarlos gráficamente, si los siguientes vectores son equivalentes:
a. MPyÑO
b.MNyPO
O
■
1
GE 1
Vectores
Vectores en el plano
GUÍA DE EJERCITACIÓN
11. Consideren los puntos A = (0; 0), B = (1; 1 ), C = (-1; 1) y D = (1; 3):
O
a. Hallen un vector con origen en C que sea equivalente a AB.
b. ¿Son paralelos A B y CD?
O
c. Hallen las coordenadas de E, tal que AB y CE sean paralelos.
O
12. Si a = ( 2; 8), b = (-1; 0), c = (3; 5), d = (-7; 3) y e = (0; -5), calculen:
a. d + e =____________________________________________________________________
b. 2 .
~a = _____________________________________________________________________
c. 3 . c + 5 . e =_
O
d .'d - 3 .'b = _
e. (a+ b ) . ( c + d) = _
f. 8 a + (-5 ). b =____
g. (4a + 5 b ) . ( c - 2 d ) = ------------------------------------------13. Sean los vectores a = (-1; 2), b = (5; 4) y c = (-5; 9), hallen:
a. a . c = __________________________________________________________
o
b. a . b = __________________________________________________________
c. b . c = __________________________________________________________
d. a . a = __________________________________________________________
_______________
1
ALUMNO
- 1
- 1
CURSO
FECHA
GE 1
GUÍA DE EJERCITACIÓN
14. Calculen a . b, sabiendo que |a| = 4 y
b = 3a.
O
15. Calculen el ángulo determinado por los siguientes vectores:
a. (5; 3) y (2; 7)
O
b. (-1; 5) y (6; 1)
16. Indiquen si los siguientes pares de vectores son ortogonales:
a. 7 = (0; -7) y b = (-7; 0 )___________________________________________
b.~a = (5 ;-2 ) y "5 = (4; 1 0 )__________________________________________
c.-7 = (2; -7) y b = (-8; 2 )---------------------------------------------
o
valor de y. Indiquen si la respuesta es única.
O
18. Hallen x para que el vector w = (x; 0) sea perpendicular a v = (-2; 3). Indiquen si la res­
17. Se sabe que el producto escalar entre a y b es 2. Si a = (4; 3) y b = (-1; y), hallen el
puesta es única.
19. Se sabe que el producto escalar entre a y b es 4. Hallen x e y siendo a = (x;y) y
"b = (x; 2).
O
■
1
GE 1
GUIA DE EJERCITACION
I
Vectores
£
Vectores en el plano
20. Hallen los ángulos del triángulo cuyos vértices son: (9; 5), (7; 3) y (4; 5).
21. Calculen los ángulos del paralelogramo cuyos vértices son (2; 7), (4; 9), (9; 1) y (11; 3).
O
O
22. Se sabe que el ángulo determinado por los vectores a y b es de 120°. Si a = (m; 2)
y b = (3; -4), hallen m.
o
23. Se sabe que los vectores v y w son ortogonales y tienen el mismo módulo. Si v = (2; 5),
hallen las coordenadas de w. Analicen si la solución es única y justifiquen su respuesta.
O
ALU M N O
CURSO
FECH A
GA 1
GUÍA DE AUTOEVALUACIÓN
1. Si ABCDEF es un hexágono regular y AB = v, BF = w y FE = u:
O
C
D
Expresar los siguientes vectores en términos de v, w y u:
ÁF =___________________________________________________________
BE =_
O
CO =
FC = _
ÉC=_
2. Dados los siguientes vectores:
O
O
a. Hallar gráficamente:
ÁB+ CD = ______________
Á C - BA =______________
b. Escribir las coordenadas cartesianas de AB:
O
c. Escribir las coordenadas polares de CD:
■
A LUM NO
■
<
CURSO
■
1
Vectores
GA1
GUÍA DE AUTOEVALUACIÓN
Vectores en el plano
3. Si A = (0; 0), B = (1; 2), C = (-1; 0) y D = (m - 1 ; m + 1), hallartodos los valores de m e IR,
tales que BA y DC sean paralelosy tengan el mismo sentido.
4. Si a = (3; 5), b = (-1; -2) y c = (0; -4), hallar:
a + b = _____________________________________________________________________________________________
7 - b = -------------------------------------------------------------------------------------------
O
3 . ("a - c) = ---------------------------------------------------------------------------------------------
T . l í = ____________________________________________________________________________________
5. Se sabe que los vectores a y b son ortogonales. Si a = (3; -4) y b = (-1 + m; -2), hallar m.
------------------------------------------------------------------------------------------------
O
6. Hallar las coordenadas de un vector que forma con v = (1; -3) un ángulo de 60°
y cuyo módulo es 5.
O
7. Hallar x para que el vector w = (x; x - 1 ) sea perpendicular a v = (-2; 3).
Indicar si la respuesta es única.
o
ALU M N O
CURSO
FECH A
MATEMÁTICA | LIBRO 4
Vectores
2 Vectores en el espacio
En algunos casos, los cuerpos están sometidos
al efecto de variasfuerzas que no pueden ser
consideradas todas en el mismo plano. Por eso
es que se hace necesario el estudio de vectores
en tres dimensiones.
M A T E M A T IC A I L IB R O 4
36
Vectores
VECTORES EN EL ESPACIO
Cuando lean el enunciado de un problema,
O Problema 1
en primer lugar, identifiquen qué es lo que
La escenógrafa de un espectáculo tiene que indicar por escrito
pregunta y qué datos pueden ser útiles
para su resolución. Posteriormente, pueden
en qué lugar exacto debe quedar suspendida una lámpara, para
representar los datos dados a través de un
que esté a cierta distancia de la mesa. ¿Cuántos datos, como
esquema. De esta manera, podrán inter­
mínimo, tiene que darle a la persona que la va a colocar?
pretarlos y relacionarlos mejor.
¿Sabían que...?
El matemático que desarrolló un cálculo
general para los vectores fue Hermann
Crassmann. Nacido en Prusia (hoy Polonia),
en 1809, Grassmann fue docente en el
Cimnasium de Stettin durante casi toda su
vida. Entre sus trabajos, se desarrolla la idea
de un álgebra en la cual los símbolos repre­
sentan entes geométricos, como puntos,
rectas y planos. Trabajó también en electri­
cidad, acústica, lingüística y botánica. Falle­
ció en Alemania, en 1877.
O Problema 2
Un grupo de investigadores está diseñando un programa de
computación, para dirigir a distancia un robot, que viajará en
una nave espacial hasta cierto lugar del espacio. Allí, deberá
salir de la nave y desplazarse hasta otro sitio. Si se toma como
punto de partida la puerta de la nave, ¿qué datos deberán
introducir en la computadora para que el robot llegue exacta­
mente a donde ellos quieren?
37
• Problema 1
La escenógrafa debe, en primer lugar, ubicar un punto de refe­
rencia, a partir del cual tomar las medidas necesarias para indi­
car exactamente dónde tiene que estar la lámpara.
Supongamos que toma el rincón derecho de la parte posterior
del escenario. A partir de allí, puede indicar cuántos centíme­
tros se deben medir por el piso hacia delante, siguiendo la pa­
red perpendicular al fondo del escenario; luego, cuántos centí­
metros sobre el piso, hacia la izquierda y, por último, cuántos
centímetros en forma perpendicular, hacia arriba.
Veámoslo en el siguiente esquema.
Ésta no es la única manera de ubicar el mismo punto. Sin em­
bargo, es necesario considerar siempre tres datos y un punto
de referencia, para que la posición sea única. Si damos sola­
mente los primeros dos datos, el punto estará en el plano
del piso; si damos otros dos, queda en otro plano, pero nueva­
mente no está definida su posición en el espacio.
Conclusión
Para definir un punto en el espacio, debemos dar un origen o
punto de referencia y un conjunto de tres datos, correspon­
dientes a direcciones ortogonales, o terna de números. A cada
uno de estos números lo llamamos coordenada.
Veamos cómo se puede representar en el espacio un punto
cualquiera. Llamemos O al origen y (xp, y^ zp) a las coordenadas
del punto P. (La disposición de estos datos es una convención.)
1. Escriban otras formas en que la esce­
nógrafa puede indicar dónde hay que
ubicar la lámpara. Por ejemplo, comen­
zando por el rincón izquierdo de la parte
de atrás del escenario.
M A T E M A T IC A I L IB R O 4
38
Vectores
VECTORES EN EL ESPACIO
2. a. Indiquen las coordenadas de los
Dibujamos tres ejes: x, y, z, perpendiculares entre sí, y traza­
siguientes puntos:
mos rectas paralelas a ellos, que pasen por las coordenadas
del punto.
O
A = (-
De esta manera, queda determinado el punto P en el espacio.
B = (-
Por ejemplo, si queremos ubicar una lámpara a 1 m de la
esquina izquierda de la pared posterior de una habitación, 2 m
b. Representen los siguientes puntos en
el diagrama anterior:
hacia la derecha y a una altura de 1,7 m, el punto sería:
C = (1; 1,5; 4)
D = (-1; 4; 2)
• Problema 2
Para lograr que el robot llegue al lugar que los científicos
proponen, los investigadores deberán indicarle la dirección
y el sentido en que deberá avanzar, y la longitud que deberá
recorrer; por lo tanto, se deberán definir los elementos de un
vector: dirección, sentido y módulo. A diferencia de los vectores
que estudiamos en el capítulo anterior, este vector está definido
en el espacio, es decir que si nos proponemos identificar el
extrem oy el origen por sus coordenadas, tendremos que dar
una terna ordenada para cada uno.
Coordenadas cartesianas
de un vector en el espacio
¿Sabían que...?
En meteorología, los vectores resultan
una herramienta útil para representar los
Representemos un vector en el espacio.
Para ello, consideremos una terna de ejes perpendiculares, con
centro en O.
vientos. Los Investigadores utilizan imáge­
nes del estado del tiempo, que reciben de
los satélites, junto con otros datos, como,
Si el vector tiene su origen en el centro de estos ejes:
por ejemplo, los mapas de vientos. En es­
tos mapas, se representa la dirección, el
sentido y la magnitud de los vientos, a tra­
©t
vés de vectores. Se dígita liza la informa­
ción que se obtiene de los satélites y, a
partir de allí, a través de diferentes algorit­
mos, se puede establecer un modelo de la
circulación atmosférica.
O
Quienes también utilizan vectores son los
navegantes, para planificar las maniobras
de sus barcos.
O
Si el vector no tiene su origen en el centro:
Si analizamos los gráficos anteriores, podemos ver que si
queremos conocer las coordenadas de un vector en el espacio,
podemos proceder de la misma forma que como lo hicimos en
el plano. Si el origen del vector coincide con el centro de coor­
denadas, O = (0 ,0 ,0 ), dicho vector queda identificado con las
coordenadas del extremo. En cambio, si el vector tiene su
origen en un punto cualquiera del espacio, podemos tomar
otro vector equivalente a él que sí tenga origen en (0 ,0 ,0 ).
¿Oué relación hay entre las coordenadas de este vector y las
del vector original? Observemos el gráfico:
Si A = ( x j y^ z j y B = (x2; y2; z2), las coordenadas del vector
equivalente con origen en (0; 0; 0) son:
M A T E M A T IC A I L IB R O 4
40
Vectores
VECTORES EN EL ESPACIO
3. Escriban las coordenadas de los
siguientes vectores:
ÁB, MN, ÁM, ÑA, BN, MB
sabiendo que A = (1; 6;- 4 ), B = (- 2 ; 5; 8),
M = ( - 5 ;2 ;- l) y N = (1; 3; 2).
Vemos que las componentes del vector son:
(x=-x b;ya-yb; za- zJ
Por ejemplo, si queremos hallar las coordenadas del vector
MN, siendo M = (3; 4; 8) y N = (0; 8; 3): MN = (-3; 4; -5).
Podemos, entonces, ampliar al espacio la definición dada en el
plano de coordenadas cartesianas (ver página 19):
Las coordenadas cartesianas o componentes de un vector
son las coordenadas del extremo de un vector equivalente
al mismo, cuyo origen es el origen de coordenadas.
Si A = (a; b; c) y P = (p; q; r), las coordenadas cartesianas
del vector AP son: AP = (p - a; q - b; r - c).
Por lo tanto, al igual que en el plano, cada vector puede identifi­
carse con un vector equivalente, con origen en (0; 0; 0), y éste, a
su vez, con las coordenadas de su extremo; entonces, cada pun­
Algo más...
to del espacio se identifica con una terna (x;y; z), y viceversa.
Sabemos que IR2y IR3 corresponden, res­
pectivamente, a los conjuntos de pares
ordenados y ternas de números reales.
Los primeros representan las dos di­
mensiones del plano y los segundos, las
tres del espacio. También se definen
IR4, IR5, IR".
IR4 es útil, por ejemplo, cuando resulta
necesario considerar lastres dimensio­
nes espaciales y el tiempo, simultánea­
mente.
Se llama IR3al conjunto de todas las ternas ordenadas de
la forma (x; y; z), con x, y, z e IR.
O Problema 3
Un juego para computadora en tres dimensiones está diseña­
do de tal forma que en el programa se consideran tres ejes
ortogonales y a cada punto se lo identifica con una terna de
números. Si el personaje del juego estaba ubicado en el punto
A = (2; 3; 5) y se desplazó hasta el punto B = (3; 7; 8), ¿qué dis­
tancia recorrió?
41
• Problema 3
Representemos gráficamente la situación:
4. Hallen la norma de los siguientes
vectores:
"a = (1 ; 3; 2)
b = (0; —1; 2)
C = ( - l;- 3 ;- 5 )
5. Hallen los vectores v = (m; -3; 4) que
verifican que | v | =5.
Para facilitar el cálculo de la longitud del vector AB, tomemos
el vector equivalente a él, con origen en el centro de coordena­
6. Hallen la norma de
das: 0 0 .
Las coordenadas de 0 0 son (3 - 2; 7 - 3; 8 - 5) = (1; 4; 3).
Sea M la proyección de O sobre el piso; entonces, M = (1; 4).
Como estamos trabajando en el plano, la distancia hasta M es
V42+ 12 = V Í7 .
El triángulo MOOes rectángulo en M; por lo tanto, si aplica­
mos el Teorema de Pitágoras en los triángulos MOOy OMP:
0 0 2 = 0 M 2+ M 0 2
(i)
ÓM2 = OP2+ PM2
(2)
y reemplazamos (2) en (i)
OO2= OP2+ PM2+ M 0 2= 42+ 12+ 32= 16 + 1 + 9 = 26
Hallamos el valor que buscamos. Por lo tanto, el personaje
avanzó a/26 unidades.
Al calcular la distancia de O a O, que es la misma que de A a B,
hallamos el módulo del vector. Cuando se trabaja con vectores
en el espacio, también se lo denomina norma del vector.
El módulo o norma del vector v cuyas coordenadas son
(x, y, z) es |"v| = V x2+y2+ z2.
Por ejemplo, la norma del vector v = (3; 9; -5) es
| v| = V32+ 92+ (-5)2 =V9 + 81 + 2 5 = V ñ 5
w = ( -2m ; V41m; 4m).
M A T E M A T IC A I L IB R O 4
42
Vectores
VECTORES EN EL ESPACIO
7. Consideren los vectores
a = (1; 6; -4), b = (-1; 2;-5),
c = (7; -7; -7) y d = (1; 6; -4). Hallen:
a. b + c =
b. c - a =
c. a + b + d =
d. a + d - c =
e. 3 . a =
Operaciones con vectores en el espacio
Las operaciones con vectores en el espacio se definen en forma
análoga a las operaciones con vectores en el plano, pero exten­
diéndolas a una coordenada más.
Suma
Seanjos vectores a = (xa; ya; z j y b= (xb; y b; zb):
7 + 7 = (x a+ xb;ya+ yb; za+ zb)
Por ejemplo: si a = (7; -2 ; 4) y b = (5; 2; -1):
7+ 7= (7 + 5; -2 + 2; 4 + (-1)) = (12; 0; 3).
f. -2 . cí=
g. 5 . b + 3 . a =
h .V Í . c - 3 . b + 2 . a =
Resta
Seanjos vectores a = (xa; ya; za) y b= (xb; y b; zb):
7 - 7 = (x a- x b;ya- y b;z a- z b)
Por ejemplo: si a = (7; -2 ; 4) y b = (5; 2; -1),
7 - b = (7 - 5; -2 - 2; 4 - (-1)) = (2;
5).
Multiplicación por un escalar
Sean el vector a = (xa; ya; za) y k e IR:
k . 7 = k . ( x a; y a; z a) = ( k . x a; k . y a; k . z a)
Por ejemplo: si a = (7; -2 ; 4),
3 . 7= 3 . (7 ;-2 ; 4) = (3 . 7; 3 . (-2); 3 . 4) = (2 1 ;-6 ; 12).
Al multiplicar un vector por un escalar se obtiene otro
vector que es múltiplo del primero.
Producto escalar
La definición es análoga a la del producto escalar de vectores
en el plano.
El producto escalar de dos vectores a y b es el número
| a| | b| eos a , siendo a el ángulo determinado por dichos
vectores. Se simboliza a . b.
a . b = |a11b| c o s a
Cuando los vectores están dados por sus coordenadas
cartesianas:
8. Consideren
los vectores:
a = (—1; 2; 3), b = (—1; —2; 0) y
C = (3; 2; -5).
Si a = (a j a2; a3) y b = (b^ b2; b3), entonces:
Hallen:
a. b=
a y b pueden escribirse como combinación lineal1de
7= (1; 0; 0), w = (0; 1; 0) yT= (0; 0; 1), de la siguiente manera:
a. c=
a = a1v + a2w + a3z
~b ,T =
b = bjV+ b2w + b3z
a . b = (ajv + a2w + a3z ) . (b1v + b2w + b3z)
9. Hallen la norma del vector
v = (n; 2 n; -n) sabiendo que
Aplicamos las propiedades distributiva y asociativa:
Indiquen si la solución es única.
V . W = 4 y W = (1; -3 ; 5).
Justifiquen la respuesta.
a . b = aja^v. v) + a ^ v . w) t a ^ f v . z) + b ^ w . v) +
+ a2b2( w . w ) + b2a3( w . z) + a3b1( z. v) + a3b2( z .w ) +
+ a3b3(T.T)
Como v, w y z son perpendiculares, entonces:
7 .7 = |7 |2 = 1, w . w = |w|2= 1 y
T.T=|T|2= 1
Además v .w = w . v = z . v = v . z = z . w = w . z = 0
10. Propongan las coordenadas de un
vector v tal que:
v . w = 5 y w = (1; -2 ; 2).
Indiquen si la solución es única.
Justifiquen la respuesta.
Conclusión
—i
Si a_= (a,; a2; a3) y b = (b ,; b2; b j, entonces
a . b = a ^ + a2b2+ a3b3.
Por ejemplo, el producto escalar entre los vectores
a = (-2; 3; 4) y b = (-5; 8 ;-1 ) es
"a . "b = (-2 ). (-5) + 3 .8 + 4 . (-1) = 30
Las propiedades del producto escalar en el espacio son análogas
a las del producto escalar en el plano2.
w Ver página 22, capítulo 1.
M A T E M A T IC A I L IB R O 4
44
VECTORES EN EL ESPACIO
11. Hallen el ángulo determinado por
los siguientes vectores:
a.'a = ( l ;- 2 ; 5) y 1) = ( - 1 ;- 6; 7)
Vectores
O Problema 4
Hallen el ángulo a tal que 0° < a < 180°, que forman los vecto­
res a y b, cuyas coordenadas cartesianas son (1; 4; 3) y (2; 3; 5),
respectivamente.
b. v = (4; -5 ; -9) y w = (0 ;- 5 ;2 )
c. m = (-5; 3; -1) y n = (-9; -5; 4)
• Problema 4
Para calcular el ángulo determinado por dos vectores en el
espacio, podemos proceder de manera análoga a la forma en
que hallamos el ángulo determinado por dos vectores en el
plano, es decir, utilizar las dos maneras de calcular el producto
escalar:
a*.
b = (1; 4; 3 ). (2; 3; 5) = 1 . 2 + 4 . 3 + 3 . 5 = 29
Calculemos los módulos de a y b:
fa| = V l2+ 42+ 32= V26
|fc>| = V22+ 32+ 52 = a/38
Por lo tanto,
29 = V 2 6 . V 3 8 . eos
eos a =
a; entonces,
29
29
V 2 6 .V 3 8 ~ 31,43
Ángulo entre dos vectores
El ángulo a que forman los vectores a y b cumple que:
eos a = .5 '
12. Indiquen si los siguientes pares de
vectores son ortogonales:
T = (1; -2; 5) y b = ( - l ; - 6; 7)
siendo 0° < a < 180°.
M l bl
Vectores ortogonales
Dos vectores a y b son ortogonales o perpendiculares
m = ( l ;2 ;3 ) y n = (0; -3 ; 2)
13. Propongan las coordenadas de
un vector ortogonal a (1; -3 ; 5).
¿Cuántos hay?
si a . b = 0. Simbólicamente, a 1 b.
Por ejemplo, los vectores v = (1; 0; 0), w = (0; 1; 0) y z = (0; 0; 1)
son ortogonales pues v . w = 1 .0 + 0 .1 + 0 .0 = 0, v . z = 0 y
z . w = 0, y como vemos en el gráfico, forman ángulos de 90°.
Algo más...
Existe una regla práctica para calcular el
producto vectorial.
Supongamos que tenemos que calcular
a x b = c, siendo a = (1; 2; 3) y
“b = (4; 5; 6).
En primer lugar, ubicamos las coordena­
das de los dos vectores en una tabla
como la siguiente:
x
y
z
5
6
1 2
4
A estos vectores se los llama versores elementales.
3
Para hallar las coordenadas de c,
tapamos la columna que contiene a
Producto vectorial
la coordenada que queremos hallar y
calculamos la diferencia ente el produc­
En el espacio, se define una nueva operación entre vectores:
to de las diagonales del cuadrado que
queda, comenzando de izquierda a
derecha. Así, se obtienen los valores de
El producto vectorial entre dos vectores a = (a^ a2; a3) y
x y de z, y el opuesto de y.
b = (b^ b2; b3) es el vector
En nuestro ejemplo:
ax b
x = 2 . 6 - 3 . 5 = -3
= {a2b3- a ib2;a3b1- a 1b,-,a1b2- a 2b1)
Por ejemplo, si a = (1; 2; 3) y b = (2; -1; -1):
7 x b = (2 . (-1) - 3 . (-1); 3 . 2 - 1 . (-1); 1 . (-1) - 2 . 2)) =
= (1; 7 ;-5 )
y = - ( 1 .6 - 4 . 3) = 8
z = 1 . 5 - 2 . 4 = -3
Luego, 7= (-3; 8; -3).
M A T E M A T IC A I L IB R O 4
46
VECTORES EN EL ESPACIO
Vectores
14. Consideren los vectores:
Propiedades del producto vectorial
J = ( l ; - 2 ; 5), b = J - l ; - 6; 7),
Sean a, b y c tres vectores en el espacio:
"v = (4; -5 ; -9) y w = ( 0 ; - 5 ; 2 ) .
Calculen:
I a x b es perpendicular a a
ax b=
Para demostrar esta propiedad, recordemos que si el producto
escalar de dos vectores es nulo, entonces los vectores son per­
ax v =
pendiculares. Por lo tanto, si demostramos que (a x b ) . a = 0,
los vectores resultan perpendiculares.
(ax
w x b=
b ). "a = (a2b3- a3b2; a3b1- a ^ ; a ^ , - a2b j . (a,; a2; a3) =
= (a2b3- a3b2) . a1+ ( a ^ - a ^ ) . a2+ (a,b2- a2b j . a3=
(aplicando la propiedad distributiva)
vxw =
= a2b3. a1- a3b2. a1+ a,b1. a2-
a1b3. a2+ a ^ . a3- a2b 1. a3= 0
Por lo tanto, los vectores son perpendiculares.
I a x b es perpendicular a b
¿Sabían que...?
El matemático que utilizó por primera vez
La demostración de esta propiedad es análoga a la anterior.
los términos producto escalary producto
vectorial fue William Kingdom Clifford,
en 1878.
Este matemático, que nació en Inglaterra
en 1845, fue un excelente alumno en la
escuela. Se destacó en diferentes áreas,
I a x b =- ( b x a )
Resolvamos por separado ambos productos, de acuerdo con la
definición:
como literatura y gim nasia,y ganó diver­
sos premios.
a x b = (a2b3- a3b2; a ^ - a ^ ; a ^ - a2b j
A los dieciocho años, ingresó en el Trinity
b x "a = (b2a3- b3a2; b ^ -
College, en Cambridge.
Fue miembro de la Royal Societyy de la
b.a,; bxa2- b2a j
Sociedad de Matemáticos de Londres.
Si comparamos los vectores, componente a componente,
Se dedicó a estudiar geometrías no eucli-
podemos ver que las coordenadas del segundo son opuestas
deanas. En uno de sus trabajos, presentó
a las del primero; por lo tanto, los vectores son opuestos.
ideas que resultaron fundamentales para
la teoría de la relatividad.
Fue docente y filósofo de la ciencia. Tam ­
bién escribió cuentos para niños.
I a x a = 0 para cualquier a
ya que:
Falleció en Portugal, en 1879.
a x a = (a2a3- a3a2; a3a1- a ^ ; a ^ - a2a j = (0; 0; 0)
que es el vector nulo.
I( a + b )x c = a x c + b x c
I Si k
e
IR: ( k . a") x 1) = k . ( T x 1>) = i T x ( k . 1))
15. Demuestren las siguientes
propiedades del producto vectorial,
enunciadas en esta página:
l(a + b )xc = axc+ bxc
I (a x b) . (a x b) = (a . a ) . ( b . b ) - ( a . b)2
I Si k 6 IR:
11ax b| = |a| |b| sen a
( k . a) x b = k . ( a x b) = a x ( k . b)
pues, si utilizamos la propiedad anterior:
l ( a x b ) . a = ( a x b). b =0
| a x b | 2 = | a x b | . | a x b | = ( a . a ) . ( b . b ) - ( a . b)2 =
I (a x b ) . (a x b) =
= | a |21 b |2 —(| a |21 b |2 eos2 oí.), aplicando la relación pitagórica:
= (a . a ) . ( b . b ) - ( a . b)2
|a x b|2 = | a|21b|2- | a| 2| b|2 (1 - s e n 2 a ); entonces,
|TxK |2= |a|2|b|2-|a | 2|b|2+ |T|2|K|2sen2a.
Por lo tanto: |a x b| = |a | | b| sen a .
O Problema 5
¿Cómo se puede hallar el área del paralelogramo ABCD
si se tienen como datos los vectores AB y AD, y el ángulo
comprendido?
• Problema 5
Para hallar el área del paralelogramo, necesitamos conocer
las dimensiones de su basey de su altura. La longitud del
segmento AB (base) es la norma del vector AB, osea, |AB|.
Para calcular la altura, analicemos el siguiente esquema:
M A T E M A T IC A I L IB R O 4
48
Vectores
VECTORES EN EL ESPACIO
16. Hallen el área del paralelogramo
Consideremos el triángulo rectángulo APD:
determinado por los vectores:
cateto opuesto
Como sen a = —¡------ E------hipotenusa
a . a - { 0 ; 2; 5) y b = (3; 2 ;-1 )
b. m = (0; -2 ; 5) y TT = (2; -1 ; 5)
| PD| = | A D | . sen a
y como a está en el primer cuadrante, sen a > 0.
Por lo tanto, el área del paralelogramo resulta:
| AB| . | AD| .sen a , que es el módulo del producto vectorial
entre A B y AD (ver página anterior).
Conclusión
17. Hallen, utilizando vectores, el área
del triángulo ABC, con A = (1; 2),
B = (2; -1) y C = (3; -1).
El área del paralelogramo que determinan los vectores a y b
es |a x £ |.
Geométricamente, el producto vectorial resulta un vector
perpendicular a los dados, cuyo módulo es:
|a x b| = |a| |b| sen a
Según vemos en el esquema anterior, dados los vectores a y b,
hay dos vectores perpendiculares a ambos con módulo | a x b|.
Hemos vistoque a x b = - ( b x a); por lo tanto, se asigna
c=axb y-c=bxa.
¡1*5 SdCiON€S
£N
lp p&füNDo!
GE 2
GUÍA DE EJERCITACIÓN
Vectores
Vectores en el espacio
1. Indiquen las coordenadas de los siguientes puntos.
O
A = (B = (-
O
C = (-
O
2. Grafiquen los siguientes puntos: A = (0; 0; 2), B = (0; 1; 0), C = (0; 0; 3), D = (2 ; -1; 2)
y E = (3; —1; -2)
O
o
49
Vectores
GE 2
GUÍA DE EJERCITACIÓN
Vectores en el espacio
3. Consideren los puntos del ejercicio anterior,
a. Escriban las coordenadas de los vectores DE, EC y EB.
b. Hallen la norma de los vectores anteriores.
4. Hallen los valores de x, sabiendo q u e | a | = 7 y q u e a = (-5; x; 3).
5. Consideren los siguientes vectores: a = (1; -2 ; -3), b = (-5; 4; -8), c = (4; -4 ; 5) y
d = (0; 0; 2). Calculen:
a. a + c = _________________________________________________________________________________
b. d - b = _________________________________________________________________________________
c. a + c + d = _____________________________________________________________________________
d. 6 . b = _
e. -7 . c =
g. 4 . c - 2 . d = ___________________________________________________________________________
h. — . "a-4"d + 5c* =_____________________________________________________________________
3
6. Consideren los siguientes vectores: a = (1; -2; 5) y b = (-2; 8; 5). Hallen c tal que
a = c - b.
ALUM N O
CURSO
FECH A
GE 2
GUÍA DE EJERCITACIÓN
7. Consideren el vector a = (1; -2; 5) y hallen c, tal que a = 3 . c.
O
.
8 Calculen la norma de a sabiendo que a + b = c, b = ( 2 ; 3 ; l ) y c = ( 4 ;7 ;- l ) .
O
9. Hallen el ángulo que determinan los vectores:
a. "v = (1 ; —3; 5) y w = ( - l;- 3 ;4 )
Q
b. "v = (2 ; 3; -7) y
C. V = (
O
0; - 1; 2)
W
= (-1; 3; -5)
y W = (- 2;
1; 8)
--------------------------------
A
10. Los vértices del ABC son A = (5; 3; 0), B = (2; -3 ; 1) y C = (-5; -2; 1). Hallen su perímetro
y la amplitud de sus ángulos interiores.
O
■
1
ALUMNO
1
Vectores
GE 2
GUÍA DE EJERCITACIÓN
Vectores en el espacio
11. Indiquen cuáles de los siguientes pares de vectores son ortogonales:
a . 7 = ( 0 ; 0 ; 2); "b = (1; 3; 5)
b.l= (-5;-l;
2); b = ( l ; 3; 4)
C. T = (4; -4 ; 2); "b = (-4; 4; 2)
12. Propongan, si existen, las coordenadas de dos vectores ortogonales a
v = (1; -5 ; -2). ¿Cuántos vectores ortogonales a v hay? Justifiquen sus respuestas.
13. Sean A = (1; -1 ; 2), B = (3; -1; 4) y C = (0; 2; 3). Hallen D, tal que:
a. AB sea paralelo a CD.
b.ABsea perpendicular a CD.
ALUM N O
CURSO
FECH A
GE 2
GUÍA DE EJERCITACIÓN
14. Sean a = (1; -3 ; -5), b = (0; -5; 6) y c = (3; -8; 4), hallen:
O
a. a . b = ________________________________________________________
b. b . c =
c. a . c =
d. c . a =
O
e. b . a i
15. Calculen el área del paralelogramo determinado por los vectores a = (2; 7; 1)
y b = (4; 9; 0).
O
O
16. Hallen un vector v perpendicular a los vectores m = (0; 1; 7) y n = (-2; 0; 4), tal que | v| = 1.
17. Se sabe que los vectores a y b son ortogonales. Si a = (3; -4 ; -1) y b = (-1 + m; -2 ; 0),
hallen m.
O
■
1
Vectores
GE 2
GUÍA DE EJERCITACIÓN
Vectores en el espacio
18. Hallen las coordenadas de un vector que forma con v = (0; -4; -3) un ángulo de 60°
y cuyo módulo es 5. ¿Es única la respuesta? ¿Por qué?
19. Hallen un vector de módulo V24 que sea perpendicular a los vectores s = (1 ; -1; 0)
y t = (8 1; 3 ,-2 ).
20. Hallen el área del paralelogramo ABCD siendo A = (1; 1; 3), B = (0; 0; 1), C = (2; 0; 3)
y D = (1; —1; 1).
21. Hallen el área del triángulo ABC siendo A = (1; 1; -4), B = (0; 0; 5) y C = (2; 0; -1).
ALUM N O
CURSO
FECH A
GA 2
GUÍA DE AUTOEVALUACIÓN
1. Sean los puntos A = (2; 3; 0), B = (-1; -3; 5), C = (5; 6; -5) y D = (-1; 0; -3):
O
a. Hallar las coordenadas de AB, BD, C A y DC.
b. Hallar la norma de cada uno de los vectores anteriores.
O
2. Dados los vectores a = (-1; -2; 3), b = (5; 0; -2), c = (-1; -1 ; 1) y d =(0; 0; 2), hallar:
a. a + c - d = ____________________________________________________________________________
O
b. 6 . b + d = _____________________________________________________________________________
c. - 7 . c - a ■
O
.. —
1 ,a +—
2 , c - 4Ad ld.
5
3
f. b . c =
g. a x c =
O
h. b x d =
■
ALUMNO
■
■
1
Vectores
GA 2
GUÍA DE AUTOEVALUACIÓN
Vectores en el espacio
3. Sean los puntos A = (1; 2; 1), B = (1; 3; -2) y C = (4; 1; -2), encontrar un vector CD
paralelo a AB cuya norma sea:
\^ )
a. mayor que la de AB
b. igual a la de AB
4. Hallar las coordenadas de un vector ortogonal a v = (1; -2; 0) cuyo módulo es V5.
O
Indicar si la solución es única.
O
5. Hallar el área del triángulo ABC, siendo A = (-1; 0; -2), B = (2; 0; -3) y C = (-2; 1; -1).
O
6. Se sabe que los vectores a y b son ortogonales. Si a = (1; -2 ; 3) y b = (1; -2 + m; 0),
hallar m.
O
ALU M N O
CURSO
FECH A
MATEMATICA | LIBRO 4
Vectores
3 Geometría analítica
La geometría analítica es la rama de la Matemá­
tica que estudia la relación entre el álgebray la
geometría.Resulta útil para programar una
computadoray ver gráficos de distintasfiguras
en tres dimensiones,ya que las rectas en el plano
y en el espacio, o los planos en el espacio, pueden
expresarse a través de operaciones entre vecto­
res. De esta manera, es posible encontrar regula­
ridadesy propiedades que los caracterizan.
M A T E M A T IC A I LIB R O 4
58
Vectores
GEOM ETRÍA AN ALÍTIC A
Es importante que cada compañero
pueda exponer sus opiniones y estrategias
para que sean analizadas portados.
Los problemas no tienen una sola forma
de encararse o de resolverse. Siempre
resulta enriquecedor escuchary analizar
cómo pensaron otros.
¿Sabían que...?
Platón nació en el año 427 a.C.y murió en
el año 347 a. C, en Atenas (Grecia). Se dedicó
a la milicia y a la política, pero la ejecución
de Sócrates, en el año 399 a. C., lo afectó
mucho e hizo que abandonara esta
última actividad.Viajó a Egipto e Italia, don­
de aprendió del trabajo de Pitágoras y co­
menzó a apreciar el valor de la Matemática.
En Atenas fundó la Academia, cuyo
objetivo era investigar e instruir sobre
Filosofía y ciencias.
Los principales aportes de Platón fueron en
filosofía, matemática y ciencias. Escribió
una serie de diálogos, en los cuales abarcó
un amplio rango de tópicos dentro de la
ética y la metafísica.
Platón consideró los objetos geométricos
como formas perfectas y buscó asociarlos
con distintos elementos. Por ejemplo,
los poliedros regulares— cubo, tetraedro,
octaedro, icosaedro y dodecaedro—
eran utilizados para representar la tierra,
el fuego, el aire, el agua y el universo,
respectivamente.
Platón decía que la matemática era de
gran importancia para proveer el entrena­
miento que necesitaba la mente y que
era fundamental para el desarrollo del su­
jeto. Una frase que le pertenece dice así:
"El propio Dios geometriza”.
O Problema 1
Gerardo está jugando con un programa de computación al que
se le introduce la información por medio de vectores. La panta­
lla muestra un sistema de ejes cartesianos con el dibujo de una
tortuga en el origen de coordenadas y un punto rojo en (3; 4).
Gerardo quiere que la tortuga camine por la recta que pasa por
el origen y por el punto rojo. ¿Cómo podría darle esta informa­
ción a la computadora, utilizando las coordenadas del punto
rojo? ¿Pasará la tortuga por el punto de coordenadas (45; 64)?
O Problema 2
En otro momento, Gerardo tiene en la pantalla a la tortuga en
el punto de coordenadas (-1; 2) y al punto rojo marcado en
(3; 4). Quiere que la tortuga camine por la recta que pasa por el
punto en donde está parada y el punto rojo. ¿Qué instrucción
podría darle a la computadora, utilizando las coordenadas del
punto rojoy del punto donde se encuentra la tortuga? ¿Pasará
la tortuga por el punto de coordenadas (19; 12)?
59
• Problema 1
Si analizamos el gráfico, observamos que entre la posición de
la tortuga y el punto, podemos definir un vector cuyas coorde­
nadas son (3; 4). Además, lo que quiere Gerardo es que la tor­
tuga se mueva desde (0; 0) sobre la recta en la que se apoya el
vector de coordenadas (3; 4).
Podemos considerar cada uno de los puntos que forman la
recta como un vector. Busquemos la forma que tienen los vec­
tores con origen en (0; 0) y con la misma dirección que el de
coordenadas (3; 4). Todos estos vectores deben ser múltiplos
de este último. Si llamamos v a estos vectores:
v = k . (3; 4) donde k es cualquier número real.
Entonces, la información que debe darle a la computadora
pueden ser distintos valores de k para realizar el producto y,
así, la tortuga irá recorriendo esta recta.
Con k > 0, se dirigirá hacia el punto rojoycon k< 0, se moverá
en el otro sentido.
Para determinar si la tortuga pasará por (45; 64), habrá que ver
si este punto pertenece a la recta, o sea, si existe un número
real k que verifique:
k. (3; 4) = (45; 64) (i)
3k = 45
4k = 64
Al resolver cada ecuación, obtenemos que en la primera, k = 15
yen la segunda, k = 16; por lo tanto, no es posible encontrar
un número real que verifique la condición (i). Entonces, dicho
punto no se encuentra en la recta, es decir, la tortuga no pasa­
rá por allí.
A esta forma de expresar la recta que pasa por el origen y
tiene la dirección del vector de coordenadas (3; 4) se la llama
ecuación vectorial.
1. Representen en el plano los vectores
que tienen la forma:
a .k ( 2 ; - l )
ke IR+
b. k (1 ; 2)
keIN
C.k(2; 1)
k e IR
d .k ( 2 ; - l ) + t ( l ; 2)
k, t e IR+
e. k [(2 ; - 1 ) + (1 ; 2)]
k e IR
f . k ( l ; 2) + (1 - k) (2; 3)
0 <k<1
M A T E M A T IC A I LIB R O 4
60
Vectores
GEOM ETRÍA AN ALÍTIC A
2. Encuentren la ecuación de las rectas
que pasan por el origen de coordenadas
y tienen dirección v.
a. v = (2 ; - 1 )
b. V = (0; 3)
C.7= (2; 0)
Ecuación vectorial de la recta
que pasa por el origen y tiene dirección v
La ecuación vectorial de la recta L que pasa por el origen
de coordenadas, con la dirección del vector v es:
L: X = k . v, con k € IR.
d .J = (0 ;-l)
e. v = (-2; 1)
3. Grafiquen las rectas encontradas en
el ejercicio anterior.
• Problema 2
En este caso, la recta por la que debe transitar la tortuga tiene
la dirección del vector con origen en A = (-1; 2) y extremo en
B = (3; 4).
4. ¿Qué pueden decir de las rectas halla­
das en a. y e. o en b. y d. del ejercicio 2?
¿Oué características tienen sus vectores
dirección?
Esta dirección es paralela a la que determina el vector con ori­
gen en (0; 0) y extremo en B - A = (4; 2).
Cada uno de los puntos que se encuentran en la recta por la
que debe caminar la tortuga puede pensarse como un vector
con origen en (0; 0). Observemos, en el siguiente gráfico, que
dicho vector es la suma de un vector de la recta que pasa por
el origen con dirección (4; 2) y el vector A.
Por lo tanto, los vectores que están en la recta que pasa por
A y por B,y que llamaremos v, se obtienen como la suma del
vector (-1; 2) y un vector de la recta que pasa por (0; 0) con
dirección (4; 2):
7 = k .(4 ;2 ) + ( - l; 2)
Tenemos, entonces, que la instrucción debe ser multiplicar
(4; 2) por cualquier número y sumarle (-1; 2).
Por ejemplo:
3 . (4; 2) + (-1; 2) = [1
-2 .(4 ; 2) + (—1; 2) = (-9 ;-2 )
son puntos que están en la recta.
Al vector de coordenadas (4; 2) se lo llama dirección de la recta.
Para determinar si la tortuga pasará por (19; 12), hay que ver si
este punto pertenece a la recta encontrada, o sea, si hay algún
número real que verifique:
k •(4; 2) + (—1; 2) = (19; 12)
4k - 1 = 19
2k + 2 = 12
Al resolver ambas ecuaciones, obtenemos k = 5; por lo tanto, el
punto se encuentra en esta recta.
Distintas formas de la ecuación de la recta
que pasa por dos puntos
5. Encuentren la ecuación vectorial de la
recta que pasa por A y B, en cada caso.
a. A = (1; 2)
B = (3; 5)
b. A = (-2; 2)
B = (4; 5)
C. A = (0; 2)
B = (-2; 4)
d. A = (-1; 3)
B = (1; 6)
6. Grafiquen las rectas encontradas en
el ejercicio anterior.
La ecuación vectorial de la recta L que pasa por los puntos
A y B es:
L: v = A + k . (B - A), con keIR
B -A e s la dirección de la recta.
Si A = (-1; 2) y B = (3; 4), la ecuación vectorial de la recta que
pasa por ambos puntos es:
L: (x; y) = k . (4; 2) + (-1; 2), con k e IR
Otra forma de caracterizar la misma recta es:
x = k .4 -1
con k e IR, que es la ecuación paramétrica.
y = k. 2 + 2
Si despejamos k en las dos ecuaciones tenemos:
x+1
y -2
k=
4
2
Por lo tanto, se debe cumplir que:
x+1 _ y -2
y ésta es la ecuación simétrica.
7. ¿Qué pueden decir de las rectas halla­
das en a .y d. del ejercicio 5? ¿Qué carac­
terísticas tienen sus vectores dirección?
M A T E M A T IC A I LIB R O 4
62
GEOM ETRÍA AN ALÍTIC A
Vectores
8. Encuentren la ecuación paramétrica
de la recta del punto a. del ejercicio 5.
Operando en esta última igualdad, se obtiene:
2(x + 1) = 4 (y-2 ) => 2x + 2 = 4y-8=>
=> 2 x -4 y = -10, que es la ecuación implícita.
Rectas en el espacio
9. Hallen la ecuación implícita de la rec­
ta del punto b. del ejercicio 5.
Si en lugar de trabajar en el plano, lo hacemos en el espacio, el
análisis es el mismo, pero los vectores tienen tres coordenadas.
Por ejemplo, si queremos encontrar la ecuación de la recta que
pasa por los puntos A = (4; 0; 3) y B = (7; 1; 5):
V = k . (B - A) + A, con k e IR
V = k . (7 — 4; 1 — 0; 5 — 3) + (4; 0; 3)
V = k . (3; 1; 2) + (4; 0; 3) es la ecuación vectorial.
10. Encuentren la ecuación simétrica de
la recta del punto c. del ejercicio 5.
11. Hallen la ecuación de la recta que
pasa por A y B, en cada caso.
a.A = (l;2 ;3 )
B = (0; 3; 6)
b. A = (0; -2; 4)
B = (-2; -5; 6)
Si V = (x; y; z), la ecuación paramétrica será:
lx = 3k + 4
6y = k
con k e IR
2z = 2k + 3
Despejemos k de cada una de las ecuaciones anteriores para
obtener la ecuación simétrica:
12. Encuentren la ecuación de la recta
representada en el siguiente gráfico:
k=
x -4
k =y
k=
z -3
x -4
z -3
3 _y_
2
En este caso, tenemos dos igualdades a partir de las cuales
obtenemos las ecuaciones implícitas.
O sea:
x -4
z -3
—
-y
y=t De la primera ecuación obtenemos x - 3y = 4 y de la segunda
ecuación, 2 y -z = -3.
Por lo tanto, las ecuaciones implícitas de esta recta pueden ser:
x - 3y = 4
2y - z = -3
Éstas no son las únicas ecuaciones implícitas, ya que, por ejem­
plo, si hubiéramos tomado:
x -4
z- 3
z -3
3 " 2 ,y _
2
las ecuaciones hubieran resultado ser:
2 x -8 = 3 z -9
2y = z - 3
O sea que:
2 x - 3z = -1
2y - z = - 3
también son ecuaciones de esta recta.
13. Hallen el vector dirección y dos pun­
tos en cada una de las siguientes rectas
del piano:
a. x + 3y = 5
b.
x-1
y +1
O Problema 3
Un juego para computadora se presenta en una pantalla plana.
En el juego intervienen una liebre, un lobo, un sapoy una rana.
a. Si se pretende hacer caminar a la liebre por una recta que
pase por A = (-1; 2) y que no se cruce con el lobo que camina
por la recta que pasa por los puntos B = (1; -2) y C = (2; 1).
¿Cuál será la ecuación de la recta por la que debe caminar la
liebre?
b. Si el sapo debe caminar por una recta L que pase por (2; 3)
y que sea perpendicular a la recta L’ de ecuación 2 x - y = 5 por
la que camina la rana, ¿cuál será la ecuación de la recta por la
que debe caminar el sapo?
x = 4A + 1
y = 3A + 2
X e IR
14. Encuentren la dirección y dos puntos
en cada una de las siguientes rectas del
espacio:
a. x = - X + 1
y =2
z = 3A - 2
• Problema 3
a. Analicemos en forma gráfica la situación:
O 1
b. f x + y = 2
2x - y + z = 0
.................................. /
to
A
1 ----------J B
1 /2
/
-2
©
~7C
2 x -3
c. — - — =
Para que, en el plano, las rectas no se crucen, deben ser parale­
las. Los vectores dirección de una recta y de la otra deben ser
paralelos. Por lo tanto, si consideramos los puntos P = ( x ; y) de
la recta por la que va a caminar la liebre como extremos de
vectores con origen en A, éstos deben cumplir, por ejemplo:
ÁP// BC.
Por lo tanto, P - A debe ser un múltiplo de C - B.
(x; y) - (-1; 2) = k[(2; 1) - (1; -2)] para algún k e IR.
y +1
=z
-3
——
M A T E M A T IC A I LIB R O 4
64
GEOM ETRÍA AN ALÍTIC A
Decidan si las siguientes rectas son
paralelas. Justifiquen sus respuestas.
15.
a. L: X = k (1; 0) + (2;-1)
L’: X = k (0; 1) + (4; -2)
k e IR
k e IR
Vectores
(x; y) = k . (1; 3) + (-1; 2), con k e IR
Observemos que esta recta tiene la misma dirección que la
que pasa por By C.
Rectas paralelas
Dos rectas son paralelas si sus vectores dirección
son múltiplos.
b. L: x - 4y = 7
L':-3x + 12y = 4
, x -1
„ z+3
c. L: — — = y + 2 = — —
3 1
2
L’: X = k (-3; -1; -2) + (1; 1; 1), k 6 IR
16. Encuentren la ecuación de una recta
que pasa por (-2; 5) y es paralela a la
recta cuya ecuación es 2x + 3y = 6.
¿Cuántas rectas hay que cumplan estas
condiciones?
Por ejemplo:
Analicemos si son paralelas las rectas:
L: V = t (2; 3) + (1; -1), con t e IR
L’: íx = k + 5
con k e IR
y = l,5 k -7
El vector dirección de L es (2; 3). Busquemos el de L’:
(x; y) = (k + 5; l,5k - 7) = (k; l,5k) + (5; -7) =
= k(l; 1,5)+ (5;-7).
El vector dirección de L’ es (1; 1,5).
Ambos vectores son múltiplos, ya que (1; 1,5) = -^(2; 3); por lo
tanto, Ly L’ son paralelas.
Para resolver la parte b. del problema 3, primero encontremos
la ecuación vectorial de la recta cuya ecuación implícita es
2 x - y = 5.
Los puntos (x; y) que pertenecen a esta recta verifican que
2 x - y = 5 =>y = 2 x - 5 =>
=> (x; y) = (x; 2x - 5) = (x; 2x) + (0; -5) = X . (1; 2) + (0; -5)
La ecuación vectorial es entonces:
(x;y) = x . ( l ; 2) + (0; -5)
Veamos el gráfico:
Los vectores que se encuentran sobre la recta L deben ser per­
pendiculares a los vectores que se encuentran sobre la recta L’.
Por lo tanto, la dirección de los primeros debe ser perpendicu­
lar a la dirección de la recta L'.
Si P= (x; y) es el extremo de un vector con origen en (2; 3) sobre
la recta L, su dirección es ( x - 2; y -3 ) ,y para que sea perpendi­
cular a (1; 2), el producto escalar debe ser 0:
( x - 2 ; y - 3). (1; 2) = 0 = > x-2 + 2 .( y -3 ) = 0=>
= > x-2 + 2 y -6 = 0=>x + 2y = 8, que es la ecuación implícita
de la recta que buscábamos.
Hallemos su ecuación vectorial:
x = 8 - 2y => (8 - 2y; y) = (-2y; y) + (8; 0) = y (-2; 1) + (8; 0)
17. Encuentren la ecuación de una recta
que pasa por (-2; 5; l) y e s paralela a la
recta cuya ecuación es
X = k(l; 1; 0) + (1; 1; 1), ConkelR
¿Cuántas rectas hay que cumplan estas
condiciones?
Observamos que las direcciones de Ly L’ son ortogonales:
(-2; 1). (1; 2) = -2 + 2 = 0
Rectas perpendiculares
Dos rectas son perpendiculares si sus vectores dirección
son ortogonales.
Por ejemplo:
Analicemos si son perpendiculares las rectas:
L: V = t (2; 3) + (1; -1), con t E IR
L’: 2x + 3y = 15
El vector dirección de L es (2; 3). Busquemos el de L’.
Despejemos x en la ecuación: x = -l,5 y + 7,5
(x; y) = (—1,5y + 7,5; y) = (-l,5y; y) + (7,5; 0) =
= y (-1,5; 1) + (7,5; 0)
El vector dirección de L’ es (-1,5; 1).
Veamos si ambos vectores son ortogonales:
(2; 3). (-1,5; 1) = 2 . (-1,5) + 3 .1 = -3 + 3 = 0; por lo tanto,
las rectas son perpendiculares.
O Problema 4
En un juego para computadora, un gato camina por la recta de
ecuación L: k(2; 3; 1) + (1; 2; 2), con ke IR, y un perro camina por
la de ecuación L’: k (-l; 1; 2) + (1; -3; 1), con k € IR.
¿Podrían encontrarse los personajes en algún lugar?
• Problema 4
En este caso, es necesario que determinemos, si existe, un
punto común entre las dos rectas.
Si (x; y; z) e L, existe un número k para el cual
(x; y; z) = k(2; 3; 1) + (1; 2; 2) = (2k + l;3 k + 2;k + 2)
18. Decidan si las siguientes rectas
son perpendiculares. Justifiquen sus
respuestas
a. L: X = k(l; 3) + (3; 2)
ke IR
L': X = k( —3; 1) + (2; 2)
,
, x -1
b. L _
_
z+ 3
. y+ 2 . _
L': X = k(2; -1 ; 0) + (2; 3; -2), con k E IR
19. Encuentren la ecuación de una recta
que pasa por (-2; 5) y es perpendicular a
la recta de ecuación 4x - 5y = 20.
¿Cuántas rectas hay que cumplan estas
condiciones?
M A T E M A T IC A I LIB R O 4
66
Vectores
GEOM ETRÍA AN ALÍTIC A
20. Encuentren la ecuación de una recta
que pasa por( 0; 1 ; 2) y es perpendicular
a la recta cuya ecuación es
X = k (1; 0; 1) + (2; -1 ; 1), con k e IR
¿Cuántas rectas hay que verifiquen es­
tas condiciones?
21. Hallen los puntos de intersección
entre las siguientes rectas:
a. L: X = k(-3;5) + (2; -4), con k e IR
L’: X = t(3;2) + (-1; 8), con t e IR
b. L: X = k(2; 1; 4) + (-1; -2 ; -13), con k 6 IR
L
x -1
: _
=
y _ _1 z + 3
=
Si (x; y; z) e L’, existe un número t para el cual
(x; y; z) = t (-1 ;1 ;2) + (1; -3; 1) = (-t + 1; t - 3; 2t + 1)
Por lo tanto, debe cumplirse que:
2k + l = - t + l=> t = -2k
(i)
3k + 2 = t - 3
k + 2 = 2t +1
Reemplazando (i) en la segunda ecuación, obtenemos:
3k + 2 = -2 k - 3 => 5k = -5 => k = -1
Reemplazando en la primera ecuación, calculamos que:
t =2
Verifiquemos si estos valores cumplen con la tercera ecuación:
k + 2 = -1 + 2 = 1
2 t+ 1 = 2.2 + 1 = 5
Como la igualdad no se cumple, podemos deducir que estas
dos rectas no se cortan; por lo tanto, los personajes no se
encuentran nunca.
Si estas rectas no se cortan, ¿serán entonces paralelas?
Para verificar esto, debemos ver si sus vectores dirección son
múltiplos:
Vector dirección de L = (2; 3; 1)
Vector dirección de L’ = (-1; 1; 2)
Podemos observar que no son múltiplos; por lo tanto,
no se cortan ni son paralelas. Este tipo de rectas se llaman
alabeadas.
_
Rectas alabeadas
Dos rectas en el espacio son alabeadas si no se cortan ni
son paralelas.
O Problema 5
En un juego para computadora, Claudio necesita marcar con
puntos verdes los extremos de los vectores del espacio que
tienen su origen en (0; 0; 0)y que son perpendiculares al vector
de coordenadas (1; 1; 2). ¿Oué condiciones deben cumplir
dichos puntos?
• Problema 5
Algo más...
¿Cómo podemos medir la distancia de
un punto a una recta en el plano?
Veamos el
O
Si el vector W = (a; b; c), con origen en (0; 0; 0), es perpendicu­
lar al vector V = (1; 1; 2), debe cumplirse que:
V . W= 0 =» (1; 1; 2). (a; b; c) = 0 =» a + b + 2c = 0
O sea, las coordenadas de W deben cumplir que:
a + b + 2c = 0
En el gráfico, podemos observar que estos puntos determinan
un plano en el espacio.
La distancia de un punto A a una recta L
es el módulo del vector con origen en A
y extremo en la intersección entre L y la
recta perpendicular a Lque pasa por A.
Por ejemplo, calculemos la distancia de
A = (4; -3 ) a la recta L: 3x - 2y = 5.
Planos en el espacio
Dados los vectores N y A en el espacio, se llama plano
ortogonal a N que pasa por A a la región formada por los
puntos X del espacio que verifican que el vector AX es
perpendicular al vector N.
En consecuencia: ( X - A ) . N = 0
De acuerdo con la definición, es necesa­
rio encontrar la recta perpendicular a L
que pase por (4;-3).
Para que las rectas sean perpendicula­
res, lo deben ser sus direcciones. El vec­
tor dirección de L es (2; 3); entonces, la
recta perpendicular tiene por dirección
(-3; 2) y pasa por (4; -3). Su ecuación
vectorial es L': X = k (-3; 2) + (4; -3).
Busquemos ahora la intersección entre
Ly L’.
El vector N se llama vector normal al plano.
En el problema 5, hallamos el plano que pasa por el origen y es
perpendicular al vector V = (1; 1; 2). Las coordenadas de los
puntos de dicho plano cumplen con la ecuación x + y + 2z = 0.
Observemos que los coeficientes de las variables x,y, z son las
coordenadas del vector normal: (1; 1; 2).
Veamos qué condición deben verificar estos puntos.
Si se despeja cualquiera de las variables, tenemos: x = - y - 2z.
Si (x; y; z) está en el pía no => (x; y; z) = (-y - 2z; y; z) =
= (-y; y; o) + (-2z; o; z) = y ( - i ; i ; o) + z(-2; o; i) =>
=> los vectores que pertenecen a este plano son combinaciones
lineales de los vectores (-1; 1; 0) y (-2; 0; 1).
Las coordenadas de los puntos de L’ tie­
nen la forma (-3k + 4; 2 k -3 ). Para que
alguno de estos puntos también esté en
L, debe verificarse que:
3 (—3k + 4) — 2(2k - 3) = 5 =>
=>-9 k + 12 - 4k + 6 = 5 => k = 1
Por lo tanto, el punto de intersección es
B = (1; -1).
La distancia es
| ÁB | = V ( 4 - l ) 2+ ( - 3 + l) 2 = 3,6
M A T E M A T IC A I LIB R O 4
68
GEOM ETRÍA AN ALÍTIC A
22. Encuentren la distancia del punto
Vectores
Planos coordenados
A = (2; - 6) a la recta cuya ecuación es
x -2
4
Se llama plano coordenado xy al plano que pasa por el
origen y su normal es el eje z.
y +1
-2
Para encontrar la ecuación del plano coordenado xy, tomemos
un vector en el eje z; por ejemplo, (0; 0; 1).
Como debe pasar por (0; 0; 0), entonces la ecuación es:
(x;y; Z ) . (0 ; 0 ; 1) = 0 = > Z = 0
Se llama plano coordenado yz al plano que pasa por el
origen y su normal es el eje x.
23. Encuentren la ecuación del plano
con normal N y que pasa por P.
Hallen tres puntos que pertenezcan a
ese plano.
a. N = (-3; 2; -1 ) P = (0; 3; -A )
Para encontrar la ecuación del plano coordenado yz, tomemos
un vector en el eje x; por ejemplo, (1; 0; 0).
Como debe pasar por (0; 0; 0), entonces la ecuación es:
(x;y; z ). (1; 0; 0) = 0=>x = 0
Se llama plano coordenado xz al plano que pasa por el
origen y su normal es el eje y.
b. N = (0; 2; 4) P = (-1; 1; 4)
Para encontrar la ecuación del plano coordenado xz, tomemos
un vector en el eje y; por ejemplo, (0; 1; 0).
Como debe pasar por (0; 0; 0), entonces la ecuación es:
(x; y; z ). (0; 1; 0) = 0 => y = 0
24. Decidan si los siguientes puntos
pertenecen al plano que pasa por
(-3; 4; 2) y cuya normal es (1; 2, -3 )
a. ( - 1 ; 0; 0)
____________
b. (0; 3; 2)
____________
C.
(0; 0; —1)
____________
25. Completen los siguientes puntos
para que pertenezcan al plano del ejer­
cicio anterior.
a .(2 ;-3 ;_ )
b. (-4 ;___; 5)
C. (------; 2; -2)
Representación gráfica de un plano en el espacio
Para realizar la gráfica de un plano en el espacio, podemos
buscar los puntos donde éste corta a los ejes.
Por ejemplo, si la ecuación del plano es 3x + y + 2z = 6, los pun­
tos que se encuentran sobre el eje x verifican que y = 0, z = 0;
entonces, para que estén en el plano, deben cumplir: 3x = 6. Se
obtiene, así, que las coordenadas del punto deben ser (2; 0; 0).
69
Los puntos que se encuentran sobre el eje y verifican que x = 0,
z = 0; entonces, para que estén en el plano, deben cumplir:
y = 6. Se obtiene, así, que las coordenadas del punto deben ser
(0; 6; 0).
Los puntos que se encuentran sobre el eje z verifican que x = 0,
y = 0; entonces, para que estén en el plano, deben cumplir:
2z = 6. Se obtiene, así, que las coordenadas del punto deben
ser (0; 0; 3).
26. Representen gráficamente los
siguientes planos:
a. 2x + 5y + 3z = 30
Qt
O Problema 6
Para realizar un decorado, una escenógrafa quiere colocar dos
planos de distinto color. Hace el diseño en una computadora
y decide marcar en rojo los puntos del plano cuya ecuación es
x + 3 y -z = ly e n amarillo, los puntos del plano que pasa por
(-1; 2; 1), (2; 1; 6) y (2; 4; 2). ¿Oué puntos quedarán pintados
de color anaranjado?
• Problema 6
Este problema plantea la intersección de los dos planos. Uno
de ellos está dado por su ecuación; luego, debemos encontrar
la ecuación del otro, que pasa por los puntos A = (1; 1; -1),
B = (0; 1; -4) y C = (1; 0; 2).
Observemos el esquema:
O
c. 3y + 2z = 12
©t
©
La normal de este plano es un vector perpendicular a AB
ya AC. Para hallarlo, podemos utilizar el producto vectorial
entre AB y AC, que cumple con esta propiedad:
N = AB x AC = (B - A) x (C - A) = (-1; 0; -3) x (0; -1; 3)
N = (-3; 3; 1)
O
o
M A T E M A T IC A I LIB R O 4
70
GEOM ETRÍA AN ALÍTIC A
¿Sabían que...?
El símbolo de paralelismo escrito en
forma vertical, //, lo utilizó por primera vez
William Oughtred en el libro Opuscula
M a them atica Hactenus Inédita, publicado
en el año 1677. Anteriormente, se utiliza­
ban como símbolo de paralelismo dos
líneas horizontales, algo parecido al sím­
bolo actual de igual.
William Oughtred nació en el año 1574, en
Eton, Inglaterra. A pesar de no recibir una
gran instrucción matemática en las escue­
las donde estudió, se interesó mucho por
esta ciencia. Fue ministro episcopal en
1603, luego fue vicario de Shalford y, en
1610, se convirtió en rector de Albury.
Oughtred tomó alumnos privados, quienes
se hospedaban en su casa y aprendían
Matemática. Algunos de ellos fueros fa­
mosos matemáticos. Su libro más impor­
tante fue Clavis M athem aticae, donde in­
cluyó una serie de nuevos símbolos, como
x para la multiplicación.
También inventó una primera forma de la
regla de cálculo.
Murió en Albury, Inglaterra, en el año 1660,
y el libro donde aparece el símbolo de pa­
ralelismo fue publicado en forma postuma.
Vectores
Por lo tanto, la ecuación del plano que es normal a N y pasa
por A es:
( X -A ) .N = 0 = > ( x - l ; y - l ; z + l) .(-3 ; 3; 1) = 0 =>
=>-3 ( x - 1) + 3 ( y - 1) + 1 (z + 1) = 0
-3 x + 3y + z = -1 =>-3x + 3y + z = -1
Plano que pasa por tres puntos
La ecuación del plano que pasa por tres puntos no
alineados A, ByCes:
( X -A ) . N = 0, donde N = ( B -A ) x ( C -A )
Volvamos al problema y realicemos el gráfico de los dos planos:
Encontremos, ahora, los puntos que pertenecen a los dos pla­
nos; o sea, los puntos (x; y; z) que verifican las dos ecuaciones
a la vez.
-3 x + 3y + z = -1
(i)
x + 3y - z = 1
(2)
Despejamos la variable z de la ecuación (2):
z = x + 3y - 1
(3)
Reemplazamos en la ecuación (1):
-3 x + 3y + (x + 3 y - 1) = -1 =>
=>-3 x + 3y + x + 3y - 1 = -1 =>-2 x + 6y = 0 =>x = 3y
Reemplazamos esta expresión en la ecuación (b):
z = 3 y + 3 y -l= > z = 6 y - l
Los puntos que quedan pintados de anaranjado son los que
verifican:
(3y; y ;6 y -l) = y ( 3 ; 1; 6) + (0; 0;-1)
La intersección de estos dos planos es la recta con vector direc­
ción (3; 1; 6) que pasa por (0; 0; -1).
Paralelismo y perpendicularidad
entre rectas y planos
27. Encuentren la ecuación del plano
que contiene a los puntos A = (-1; 2; 0),
B = (1; 1; 2) y C = (0; 1; 1).
Dos planos son paralelos si sus vectores normales son
múltiplos.
28. Hallen la ecuación del plano que
ir
contiene a las rectas Ly L’, donde:
L: X = k (1; -1 ; 0)
k G IR
L’:X = t(3 ;2 ;2 ) + (0 ;-5 ;-2 ) t G IR
Por ejemplo, los planos:
TT: 2x + By + 4z = 2 y TT’: 4x + 6y + 8z = 5
son planos paralelos, ya que la normal de TT es (2; 3; 4) y la nor­
mal de TT’ es (4; 6; 8), que son múltiplos.
Dos planos son perpendiculares si sus vectores normales
son ortogonales.
ir
Por ejemplo, los planos:
TT : 4x + 3y + 3z = 9 y TT’: 3 x - y - 3 z = 5
son perpendiculares pues la normal de TT es (4; 3; 3)y la
normal de TT’ es (3; -1; -3).
Calculemos el producto escalar para verificar que son vectores
ortogonales:
(4; 3; 3). ( 3 ; - l; -3) =4. 3 + 3 . (-1) + 3 . (-3) = 1 2 -3 -9 = 0
29. Hallen los puntos que se encuentran
en la intersección de los siguientes
planos:
TT: 2 x - y + z = 3
TT': - x + y = 0
30. Encuentren los puntos que pertene­
cen a la intersección del plano TT y la
recta L:
T T : x -y + z = 3
L: recta que pasa por (1; 1; 2) y (0; 1; -1 )
M A T E M A T IC A I LIB R O 4
72
GEOM ETRÍA AN ALÍTIC A
31. Encuentren la ecuación de un plano
que pase por el punto (2; -2 ; 5) y sea
paralelo al plano de ecuación
2x + y + 5z = 7. ¿Cuántos planos hay
que cumplan estas condiciones?
Vectores
Una recta es paralela a un plano si la dirección de la recta
es perpendicular a la normal del plano.
h
v
L
N
n
32. Encuentren la ecuación de un plano
que pase por el punto (-1; 1; 3) y sea
perpendicular al plano de ecuación
x + y + z = 0. ¿Cuántos planos hay que
cumplan estas condiciones?
33. Encuentren la ecuación de una recta
que pase por el origen y sea paralela al
plano que pasa por los puntos (1 ; 1 ; 1 ),
(2; 0; -1 ) y (0; 0; 2). ¿Cuántas rectas hay
que cumplan estas condiciones?
n
Por ejemplo:
L: V = k(l; -1; -2) + (3; 4; 6), con k € IR
TT: x - 3y + 2z = 7
La dirección de la recta L es (1; -1; -2) y la normal del plano TT
es (1; —3; 2).
Calculemos el producto escalar para constatar si los vectores
son perpendiculares:
(1 ;-1 ;-2 ). (1;-3; 2) = l + 3 -4 = 0
Como la dirección de la recta y la de la normal del plano son
perpendiculares, la recta es paralela al plano.
Una recta es perpendicular a un plano si el vector
dirección de la recta es múltiplo de la normal del plano.
N
34. Hallen la ecuación de una recta
que pase por el punto (1 ; 1 ; 1 ) y sea
perpendicular al plano cuya ecuación es
2 x - y + z = 4. ¿Cuántas rectas hay que
cumplan estas condiciones?
V
1
n
Por ejemplo:
L: V = k(0; 2; 1) + (3; 3; -4), con k e IR
TT: 6y + 3z = 15
La dirección de la recta L es (0; 2; 1) y la normal del plano TT es
(0; 6; 3). Estos vectores son múltiplos; por lo tanto, la recta y el
plano son perpendiculares.
GE 3
GUÍA DE EJERCITACIÓN
Vectores
Geometría analítica
1. Encuentren las ecuaciones de las rectas que verifican cada una de las siguientes
condiciones. Grafiquen, en cada caso, la recta hallada.
a. M pasa por los puntos A = (2; -4) y B = (-6; 4).
b. R pasa por el punto C = (1; -4) y por el origen de coordenadas.
c. T es paralela a la recta M y pasa por el punto D = (2; 5).
O
O
o
2. Encuentren la ecuación vectorial de las siguientes rectas del planoy tres puntos que
pertenezcan a cada una de ellas,
a. x - 6y = 12
b.
2- x
6
y+ 4
“
c. x = 2t - 5
y = 4 - 5t
O
-2
te IR
73
GE 3
Vectores
Geometría analítica
GUIA DE EJERCITACION
3. Encuentren las ecuaciones de las rectas que verifican cada una de las siguientes
condiciones. Grafiquen, en cada caso, la recta hallada,
a. S pasa por los puntos A = (2; 1; 4) y B = (4; 6; 2).
O
b. H tiene vector dirección (2; 3; 4) y pasa por el punto (1; 1; 1).
c. F es paralela a la recta S y pasa por el punto (3; 4; 1).
O
O
4. Encuentren la ecuación vectorial de las siguientes rectas del espacioy tres puntos que
pertenezcan a cada una de ellas.
a.
O
x- 2
y +1
z
-3 “ 2 “ “4
x +y -z =4
x +y = 2
x =2
y = 2+t
z=3
ALU M N O
O
te IR
CURSO
FECH A
GE 3
GUÍA DE EJERCITACIÓN
O
5. Analicen si la recta cuya ecuación vectorial es X = k(2; -2; 4) + (-1; 1; -2), con k e IR, pasa
por el origen de coordenadas.
6. Encuentren la ecuación de la recta que pasa por (-2; l)y e s perpendicular a la recta cuya
ecuación es 2x + 3y = 6.
O
7. Hallen la distancia del punto (4; 4) a la recta cuya ecuación es
x -2
y +1
3 “ -2
O
8. Encuentren, si existe, la intersección entre las siguientes rectas del plano:
a. L: x - y = 2
O
b. L: x = 2
y = 2 + t te IR
L’: x -2 : y +1
L’: X = k (0, 2) + (1; 1) k e IR
9. Encuentren, si existe, la intersección de las siguientes rectas del espacio:
a. L: x + 2y = 0
2x - z = 1
L’: X = k(l; -1; 0) + (0; 1; 3) k E IR
O
■
1
I
GE 3
GUIA DE EJERCITACION
b. L:
= 2 + 2t
y = 3- t
te IR
z =t
X
1
Vectores
Geometría analítica
L’: X = k(l; 3; 2) + (4; 2; 2) k e IR
O
10. Determinen si las rectas del ejercicio anterior son paralelas, alabeadas o se cortan en
algún punto.
O
11. Encuentren la ecuación de los planos que verifiquen las siguientes condiciones y exhi­
ban tres puntos que pertenezcan a cada plano,
a. (-3; 2; 0) es la normal y pasa por el punto (1; 1; 1).
O
b. Pasa por los puntos (2; 2; -3), (-2; 1; 1) y (0; 1; 2).
____________________________________________________________________________
O
c. Contiene a la recta L: k(l; 2; 1) + (1; 1; -1), con k e IR, y al punto (4; 1; 0).
d. Contiene a las rectas Ly L’, donde:
X + 2y = 0
2 x -z = 1
L’: X = k(l; -1; 0) + (0; 1; 3) k e IR
O
ALU M N O
CURSO
FECH A
GE 3
GUÍA DE EJERCITACIÓN
O
12. Encuentren la ecuación de una recta que pasa por el punto (0; 0; 1) y es paralela al plano
cuya ecuación esx + y + z = 3. ¿Es única esta recta? Si no lo es, muestren por lo menos dos
rectas diferentes.
O
13. Hallen la ecuación de una recta que pasa por el punto (-1 ;2; 2) y es perpendicular al
plano cuya ecuación es 2 x -y + z = 4. ¿Es única esta recta? Si no lo es, muestren por lo
menos dos rectas diferentes.
O
14. Encuentren la ecuación de un plano que pase por el punto (2; 2; 0) y es paralelo al
plano que pasa por los puntos (1; 1; 1), (0; 0; 2) y (1; 0; 1).
o
15. Encuentren la ecuación de un plano que pasa por el punto (1; 0; 1) y es perpendicular al
plano que pasa por los puntos (2; 2; 2), (-1; 1; 0)y (2; 0; 0).
O
■
1
ALUM N O
1
GE 3
Vectores
Geometría analítica
GUIA DE EJERCITACION
16. Encuentren la intersección entre los siguientes planos:
a. TT: 2 x -y + z = 0
TT’: 3x + 2y- z = 5
b. TT:x + 3 y-2 z = 4
TT’: 3x + 9y - 6z = 10
O
O
17. Encuentren la intersección entre la recta Ly el plano TT, donde:
L: X = k (-5; 4; 1) + (-1; 1; 0) k e IR
TT: 3x - 4y = -69
O
18. Determinen si la recta Lestá contenida en el plano TT, donde:
, x+ 3
L:
=y = z - l
TT:y + z = 3
O
19. Determinen si la recta Lestá contenida en el plano TT, donde:
L :x -2 = y + 4 = z - l
TT:-y + z = 5
O
ALU M N O
CURSO
FECH A
GA 3
GUÍA DE AUTOEVALUACIÓN
O
1. Completar, si es posible, las coordenadas de los puntos para que pertenezcan a la recta o
al plano indicado.
a. (2;__ ) en la recta L: X = k (-1; 2) + (3; 4), con k e IR
b. (__ ; -1) en la recta L:
x -1
y +2
3 “ ~4~
c. (1; 2;__ ) en la recta L: X = k (2; 4; -8), con k e IR
O
d. (2;__ ; -1) en la recta L:
3y - x = 4
x - z = -3
/,
.
,
. , x +4
y -1
e. (-1 ;__ ; __ ) en la recta L: _2 = J 2 = -z
O
f. (2 ;-6 ;__ ) en el plano TT: 2 x -7 y + 4z = 10
2. Determinar la ecuación de la recta que pasa por el punto de intersección entre Ly L’, y es
paralela a la recta que pasa por los puntos (2; 1) y (-3; 4), donde:
L: X = k(2; 2) + (1;-1) k E IR
L: -x g+ 2
- = y + c6
o
3. Encontrar una dirección para cada una de las siguientes rectas del espacio. Escribir su
ecuación vectorial y hallar tres puntos que pertenezcan a cada recta.
a. L: y - 3 x = 6
2x - 3z = -6
O
■
ALUMNO
■
■
1
GA 3
Vectores
Geometría analítica
GUÍA DE AUTOEVALUACIÓN
b. L pasa por los puntos (2; -3; 7) y (4; 6; -3)
, 2x + 3
3 y- 5
—
4 - 6
C. L : —
z+2
5
= — =—
4. Hallar la ecuación del plano que pasa por los puntos (2; 1; 1), (1; 1; 1) y (0; 1; 2).
5. Encontrar una recta que pase por el punto (0; 2; -2) y sea perpendicular al plano del
ejercicio anterior.
O
o
6. Encontrar la intersección entre el plano del ejercicio 4. y la recta del ejercicio 5.
o
7. Encontrar la ecuación de una recta que pasa por (2, -3; 0) y es paralela a la intersección
de los planos TT y TT’, donde:
TT:x + y + z = 3
TT’: 2 x - y - z = 0
O
ALU M N O
CURSO
FECH A
MATEMÁTICA | LIBRO 4
Vectores
4 Cónicas
Las cónicas son las curvas más importantes que
ia Geometría le ofrece a la Física,ya que, por
ejemplo, sus propiedades son de gran utilidad en
Óptica. También son utilizadas en Astronomía,
pues las órbitas de los planetas girando alrede­
dor del Sol son elipsesy, en general, la trayectoria
de cualquier cuerpo sometido a unafuerza gravitatoria es una curva cónica.
82
CÓNICAS
A medida que resuelvan un problema, pre­
gúntense porqué pueden hacer cada paso.
Ésta es la forma de entender y poder justi­
ficar los procedimientos que realizan.
O Problema 1
Un faro construido en el centro de una isla desierta gira sobre
su eje y emite un haz de luz con un alcance de 100 m. ¿En qué
lugar debe ubicarse un barco para atrapar el extremo del haz
de luz?
¿Sabían que...?
Edmond Ha Iley nació en Haggerston,
Inglaterra, en 1656. Estudió en Oxford
y a los 22 años ingresó en la Royal Society.
En sus actividades, influyeron las publica­
ciones de Apolonio de Perga y otros anti­
guos geómetras griegos.
En 1686, publicó el primer mapa meteoro­
lógico.
En 1705, predijo que el cometa que había
cruzado el cielo en 1682 volvería a hacerlo
en 1758, y que era el mismo que había
pasado en 1531 y 1607. Descubrió, así, que
los cometas tienen una trayectoria pareci­
da a la de los planetas, pero que se acercan
y alejan del Sol mucho más que ellos.
Murió en 1742 sin ver que el 25 de diciem­
bre de 1758 su predicción se cumplió.
El cometa en cuestión lleva su nombre: es
el cometa Ha Iley.
Este cometa fue visto por última vez en
1986 y se prevé que volverá en el año 2061.
O Problema 2
Consideren el punto P = (1; 2).
a. Encuentren todos los puntos que estén a 3 unidades de dis­
tancia del punto Py cuya abscisa sea x = 0.
b. Encuentren todos los puntos que estén a 3 unidades del
punto Py cuya ordenada sea y = 6.
c. Encuentren una expresión que relacione las coordenadas de
los puntos del plano que estén a 3 unidades de distancia del
punto P.
83
• Problema 1
Si ubicamos al faro como centro de un sistema de ejes carte­
sianos, notamos que el barco debe ubicarse a 100 m del cen­
tro, en cualquier sentido. O sea:
Queda formada, así, una circunferencia con centro en el faro y
radio 100 m. Es decir que el barco puede ubicarse en cualquie­
ra de todos los puntos del plano que cumplen con la propiedad
de estar a 100 m de distancia del faro.
Lugar geométrico
Llamamos lugar geométrico al conjunto de puntos del
plano que cumplen cierta propiedad.
Circunferencia
Llamamos circunferencia al lugar geométrico de todos
los puntos del plano que están a una distancia fija, r, de
un punto dado, P.
El punto P se llama centro de la circunferencia y la distan­
cia r, radio.
1. Una escalera de una sola hoja está
apoyada sobre una pared. La escalera
tiene nueve escalones. En la mitad del
quinto escalón hay una hormiga. La
escalera comienza a deslizarse hacia
abajoy la hormiga se paraliza del susto.
¿Cuál es el recorrido de la hormiga has­
ta llegar al suelo?
M A T E M A T IC A I LIB R O 4
84
CÓNICAS
¿Cómo se lee?
dist(P,0) = distancia entre los puntos P yO .
2. Encuentren gráfica y analíticamente
el lugar geométrico de los puntos del
plano cuya distancia a (1 ; - 2) sea la mis­
ma que a (1; 5).
Vectores
• Problema 2
a. Los puntos que están a 3 unidades de (1; 2) son los puntos
que se encuentran en la circunferencia de centro (1; 2)
y radio 3. Analicémoslo en un sistema de ejes cartesianos.
Llamemos O al punto pedido. Dado que x = 0,0 = (0;y)y, ade­
más, la distancia entre Py Odebe ser 3.
O
Q - (0;y>
\
y -2
3. Encuentren gráficamente el lugar
geométrico de los puntos del plano
cuya distancia a la recta de ecuación
y = x + 1 sea la misma que a la recta
de ecuación y = - x + l.
P = f1;71
5
-5
-♦
-3
-2
-1
¡
■
■
(
Queda formado un triángulo rectángulo cuyos catetos miden
1 e ( y - 2), con lo cual, por el Teorema de Pitágoras:
dist(P, O) = V(1 - O)2+ (y - 2)2
En general:
La distancia entre dos puntos P = (Xj, y j y O = (x2, y2) es:
dist(P, O) = V(x2- x J 2+ (y2- y j 2.
En nuestro problema, queremos que dist(P, O) = 3.
Luego: V ( l- 0 ) 2+ (y -2 ) 2= 3.
Elevamos ambos miembros al cuadrado y obtenemos:
(1 -0 )2+ (y -2 )2= 9
Despejamos y:
( y - 2)2= 8 => |y- 2| =V8 = 2V2=>
= > y-2 = 2V2 ó y - 2 = -2V2=>y=2-2V2 ó y = 2 + 2V2 =>
=^>O = (0; 2 —2V2 ) Ó O = (0; 2 + 2V2 )
Encontramos, entonces, dos puntos de abscisa x = 0 que distan
3 unidades de P.
b. Busquemos ahora un punto R = (x; 6) que verifique:
dist(P, R) = 3
V ( l - x ) 2+ (2 -6 )2= 3
Elevamos ambos miembros al cuadrado:
(1 - x)2+ (2 - 6)2= 9
Operamos y simplificamos:
(1 - x)2+16 = 9 => (1 - x)2= 9 -1 6 = -7 => (1 - x)2= -7.
Pero ( l - x ) 2es positivo, por ser un cuadrado, con lo cual nunca
puede dar-7.
O sea, no existe ningún punto con ordenada y = 6 que esté a 3
unidades de distancia de P.
c. Busquemos ahora todos los puntos O = (x;y) que estén a 3
unidades de distancia de P.
dist(0, P) = 3
V ( x - l ) 2+ ( y -2 )2= 3
Elevamos ambos miembros al cuadrado:
(x - 1)2+ (y - 2)2= 9
Encontramos, entonces, una fórmula que nos permite expre­
sar una relación entre las coordenadas de los puntos O = (x; y)
que pertenecen a la circunferencia.
4. Dibujen con regla y compás, si existe,
una circunferencia que pase por los
puntos A y B. Expliquen cada paso.
¿Es única la circunferencia? ¿Porqué?
•B
A»
5. Dibujen con regla y compás, si existe,
una circunferencia que pase por los
puntos A, B y C. Expliquen cada paso.
¿Es única la circunferencia? ¿Porqué?
•B
A»
•C
Este razonamiento podemos hacerlo de forma similar, cual­
quiera sea el centro y el radio.
6. Dibujen con regla y compás, si existe,
Conclusión
Los puntos (x; y) que pertenecen a la circunferencia de centro
P = (x„; y„) y radio r verifican la ecuación:
( x - x 0)2+ ( y - y 0)2= r2
una circunferencia que pase por los
puntos A, B y C. Expliquen cada paso.
¿Es única la circunferencia? ¿Porqué?
•B
O Problema 3
¿Las siguientes fórmulas:
•C
a. x2+ y2+ 2x - 6y + 9 = 0
b. x2+ y2+ 2x - 6y + 12 = 0
son las ecuaciones de alguna circunferencia?
• A
M A T E M A T IC A I LIB R O 4
86
CÓNICAS
7. Encuentren todos los puntos que es­
tén a 2 unidades de distancia de (4; 5) y
cuya ordenada sea y = 5,5.
8. Encuentren todos los puntos que es­
tén a 2 unidades de distancia de (4; 5) y
cuya abscisa sea x = 3.
9. Determinen si el punto (2; 5) está en
la circunferencia de radio 2 y centro
(4; 5). Justifiquen su respuesta.
Vectores
• Problema 3
Si las fórmulas dadas representan una circunferencia, enton­
ces, se deben poder escribir como:
(x -x „ )2+ ( y - y 0)2= r2
(i)
donde (x0; y 0) es el centro y r el radio.
Desarrollemos la ecuación (i):
x2- 2xx0+ x02+ y2- 2yy0+ y02= r2
x2- 2xx0+ x02+ y2- 2yy0+ y02- r2 =0 (2)
Comparando la ecuación a.: x2+ y2+ 2x- 6y + 9 = 0 con la
ecuación (2), obtenemos que debe verificarse:
-2 x„ = 2 =>x0= -1
-2 y 0= -6=>y0= 3
xo2+yo2- r2= 9
p)
Si reemplazamosx0e y0en (b),queda l + 9 - r 2= 9=>r = l ó
r = -1; pero r es positivo por ser una distancia => r = 1.
Comparando b. con (2), debe verificarse:
-2 x0= 2 =>x0= -1
-2 y 0= -6=>y0= 3
x02+ y02- r 2= i2
=> r2= x02+ y02-1 2 = 1 + 9 -1 2 = -2 => r2= -2 y esto no puede
ocurrir dado que r2es positivo para cualquier valor de r.
O sea que la fórmula a. corresponde a una circunferencia de
centro (-1; 3) y radio 1. En cambio, la fórmula b. no correspon­
de a ninguna circunferencia.
O Problema 4
10. Encuentren la fórmula que vincula
las coordenadas x e y de todos los pun­
tos que estén a 2 unidades de distancia
de (4; 5).
En un club de campo, no permiten perros sueltos. Por ese mo­
tivo, la familia López decidió atar a su perro en el jardín de la
siguiente manera: clavaron dos estacas en el pasto y ataron en
ellas los extremos de una soga. En la soga hay una argolla en la
que se sujeta el collar del perro. ¿Cuál será la región del jardín
en la que el perro puede moverse?
• Problema 4
Para analizar gráficamente el problema, consideremos un sis­
tema de ejes cartesianos donde el eje x sea la recta que pasa
por las dos estacas y tracemos el eje y como una recta perpen­
dicular a la anterior, que pasa por el punto medio del segmen­
to que une las estacas.
11. Encuentren el radio y el centro de
las siguientes circunferencias:
a. x 2 + 6 x -4 y + y 2 + 5 = 0
b. x 2 + y 2- 18y -1 4 = -49
El límite del sector por donde se puede mover el perro está
formado por los puntos P que verifican que la suma de las
distancias de P a cada una de las estacas es igual a la longitud
de la soga.
12. Encuentren gráfica y analíticamen­
te, si los hay, el o los puntos de intersec­
ción entre las circunferencias del pro­
blema anterior
Elipse
Llamamos elipse al lugar geométrico de los puntos del
plano, tales que la suma de las distancias a dos puntos
fijos A y B sea constante.
Los puntos A y B se llaman focos. El punto medio entre
A y B se llama centro. La recta que contiene a los focos
se llama eje mayor.
13. Dados los puntos (1; 5), (0; 5),
| ; - 1 .(1; 2), (-4 ;-3 )y (3; 1),determi­
nen cuáles están dentroy cuáles fuera
de la circunferencia de centro (1; -3 ) y
radio 5.
O Problema 5
Dados los puntos del plano A = (2; 0) y B = (-2; 0), encuentren
una fórmula que nos permita relacionar las coordenadas de
todos los puntos P = (x; y) del plano, tales que el perímetro del
triángulo ABP sea de 20 unidades.
88
CÓNICAS
¿Sabían que...?
Johannes Kepler nació el 27 de diciem­
bre de 1571 en Weilder Stadt, Alemania.
Gracias a que los duques de W ürttemberg alentaron su educación, pudo ter­
minar sus estudios en el seminario teo­
lógico y graduarse en la Universidad de
Tubinga. Allí, su profesor le enseñó las
ideas de Copérnico, prohibidas en la
época.
Cuando todos creían que sería sacerdo­
te, Kepler aceptó un trabajo como maes­
tro de Astronomía y Matemática,y se
fue a Graz (Austria).
En 1596, creyó haber descubierto el
orden fundamental que servía de base a
las distancias que separaban a los plane­
tas del Sol. Si bien su teoría era errónea,
logró ser conocido por los grandes astró­
nomos de la época, y el 1 de enero de
1600 se fue a trabajar con Ticho Brahe,
astrónomo de la corte de Rodolfo II de
Praga, huyendo de la persecución reli­
giosa a la que fue sometido por ser pro­
testante. En 1601, murió Brahe y Kepler
asumió como matemático imperial.
Sus problemas de vista lo llevaron a in­
teresarse en la óptica. Así, escribió tra­
bajos acerca del modo en que ayudan
los anteojos a los miopes y logró el
principio de las cámaras fotográficas. En
su libro A stron om ía nova, enunció las
primeras leyes referentes a las órbitas
de los planetas.
En Matemática, contribuyó a crear el
cálculo infinitesimal y a estimular el uso
de los logaritmos en los cálculos.
Para su lápida escribió:
"Medí los cielos,y ahora las sombras mi­
do. En el cielo brilló el espíritu. En la tie­
rra descansa el cuerpo”.
Murió el 15 de noviembre de 1630 en
Ratisbona, Alemania.
Vectores
• Problema 5
Para hallar una fórmula que nos permita relacionar las coorde­
nadas de todos los puntos P = (x; y), tales que el perímetro del
triángulo APB sea 20, sabemos que:
dist(P, A) + dist(P, B) + dist(A, B) = 20
dist(P, A) + dist(P, B) + 4 = 20
dist(P, A) + dist(P, B) = 16
V ( x -2 ) 2+ ( y -0 ) 2+ V(x + 2)2+ ( y -0 ) 2= 16 => distribuyendo
obtenemos: V x2- 4 x + 4 + y 2+ V x 2+ 4x + 4 + y 2 = 16.
Si elevamos ambos miembros al cuadrado, nos queda:
(Vx2- 4 x + 4 + y 2)2+ 2Vx2- 4 x + 4 + y 2V x 2+ 4 x + 4 + y 2+
+ (Vx2+ 4 x + 4 + y 2)2 = 256
Operamos:
x2-.45< + 4 + y2+ x 2+-45( + 4 + y2+
+ 2Vx2- 4 x + 4 + y 2V x 2+ 4x + 4 + y 2 = 256
Agrupamos las raíces cuadradas y dividimos ambos miembros
por 2:
V x2- 4 x + 4 + y 2V x 2+ 4x + 4 + y 2 = 124- x 2- y 2
Si elevamos nuevamente ambos miembros al cuadrado,
nos queda:
(x2- 4x + 4 + y 2) (x2+ 4x + 4 + y 2) = (124 - x 2- y 2)2
Entonces, distribuyendo, simplificando y agrupando,
obtenemos:
8x2+
+ 8y2+ 16 + jf= 15376
248x2248y2+ 2x2y r
240x2+ 256y2= 15360
Por último, dividimos toda la ecuación por 15360:
que es la forma más simple de la ecuación buscada.
Observemos que si y = 0, los puntos P son (8; 0) y (-8; 0), que
para nuestro problema no tienen sentido, dado que APB no
sería un triángulo; y si x = 0, tenemos los puntos (0; V60) y
(0; -V60).
Encontramos una ecuación que relaciona las coordenadas de
todos los puntos P del plano, tales que la suma de las distan­
cias de P a A = (2; 0) y de P a B = (-2; 0) sea 16. Estos puntos,
geométricamente, representan una elipse.
14. Calculen el perímetro del triángulo
cuyos vértices son A = (1; 3), B = (-1; 5) y
C = (3; 8).
O Problema 6
Encuentren la relación entre las coordenadas de los puntos
que pertenecen a la elipse de focos A = (c; 0) y B = (—c; 0)
con c > 0.
• Problema 6
El eje mayor de la elipse es la recta que contiene a A y a B; en
este caso, es el eje x.
Si P = (x;y) es un punto cualquiera de la elipse, debe verificarse
que: dist(P, A) + dist(P, B) = k, siendo k constante.
Consideremos el punto de la elipse que corta el eje mayor en
el semiplano positivoy llamémoslo O; entonces, O = (a; 0)
con a > 0 y a > c.
dist(0, A)+ dist(0 ,B) = V(a - c)2+ V(a +c)2= a - c + a + c = 2a
Luego, como la suma de las distancias es la misma cualquiera
sea P, dist(P, A) + dist(P, B) = 2a, para cualquier P perteneciente
a la elipse.
16. Dados A = (4; 7) y B = H ; 7),
encuentren cinco puntos P del plano,
tales que el perímetro del triángulo APB
sea 40.
M A T E M A T IC A I LIB R O 4
90
CÓNICAS
17. Hallen la fórmula y la gráfica de la
elipse que verifica que la suma de dis­
tancias a A = (8; 0) y a B = ( - 8; 0) sea 20.
18. ¿Cuál será el lugar geométrico de los
puntos del recorrido de la hormiga de la
actividad 1. de la página 83, si en lugar
de estar en la mitad del quinto escalón
estuviera en la mitad del tercero?
Dibújenlo.
Vectores
Entonces:
V(x - c)2+ y2+ V(x + c)2+ y 2= 2a =>
^ V ( x - c ) 2+y2= 2 a -V (x + c)2+ y2
Si elevamos al cuadrado ambos miembros de la última expre­
sión y operamos, obtenemos:
(x - c)2+
4a2+ (x + c)2+ ¿ f - 4aV(x + c)2+y2
-x2'- 2xc +,e2"= 4a2+^cJ'+ 2xc +-e2'- 4aV(x + c)2+ y2
Al cancelary agrupar, queda:
-4xc - 4a2= -4aV(x + c)2+y2
Si dividimos ambos miembros p o r-4 y agrupamos, obtenemos:
xc + a2= aV(x + c)2+y2
Volvemos a elevar ambos miembros al cuadrado y operamos:
x2c2+ 2xca2+ a4= a2[x2+ 2xc + c2+ y2]
x2c2+ 2x cZ? + a4= a2x2+ 2xcSp + a2c2+ a2y2
Si agrupamos, obtenemos:
a4- a 2c2= x 2(a2- c 2) + a y
y sacando factor común en el primer miembro:
a2(a2- c2) = x2(a2- c2) + a2y 2
Dividamos ambos miembros por a2(a2- c 2) * 0, dado que a > 0
ya#c:
Si llamamos b2= a2- c 2, entonces se tiene la fórmula:
Conclusión
Si en una elipse los focos A y B están sobre el eje x y son simé­
tricos respecto del origen, sus coordenadas son A = (c; 0) y
B = (-c; 0), con c > 0. Entonces, los puntos (x; y) que pertenecen
a la elipse verifican la fórmula:
donde a es la intersección de la elipse con el semieje positivo
de las abscisas, b es la intersección con el semieje positivo de
las ordenadas y b2= a2- c 2.
91
Si, en cambio, el eje mayor estuviera sobre el eje y, sería b > a, y
los focos serían A = (0; c) y B = (0; -c).
Con un desarrollo análogo al anterior, obtenemos la fórmula
de la elipse:
19. Encuentren la fórmula de una elipse
cuya gráfica sea:
x
v
u í = 1,con a2= b2- c2
a2 + b2
-7
Supongamos que tenemos una elipse cuyo eje mayor es hori­
zontal (no necesariamente el eje x); entonces, los focos son:
A = (xi; y j y B = (x2; y j . Luego, el centro es el punto (x0; y0)
conx0= ^ (xx + x 2) e y0= y r
Tomemos, entonces, la mediatriz del segmento AB, o sea, la
recta perpendicular a AB que pasa por su punto medio, (x0; y0).
Queda formado un sistema de ejes cartesianos cuyo centro es
b.
(x0;y<,)-
20. Encuentren de manera gráfica
y analítica la intersección entre las
siguientes elipses:
Tomando c = ^dist(A, B), entonces en el nuevo sistema de
T + y 2=1
coordenadas A = (c; 0) y B = (-c; 0); por lo tanto, la ecuación de
ex2 B2
la elipse en este sistema es ~^r +
= 1-
Si ahora volvemos al sistema original, a = x - x 0, p = y - y 0.
Si el eje mayor lo tomamos en dirección vertical, podemos ha­
cer un razonamiento análogo.
Conclusión
La ecuación de la elipse de focos A y B es:
(x-x„)*
a2
(y -y ,)2
b2
l
donde (x„; y„) es el punto medio entre A y B, c = y dist(A, B)
y a2= b2- c2.
M A T E M A T IC A I LIB R O 4
92
Vectores
CÓNICAS
O Problema 7
Algo más...
Dadas las ecuaciones:
a. 4x2+ 9 y 2+ 8x - 32 = 0
b. 4x 2+ 9 y 2+ x + 3 = 0
¿Podemos saber si corresponden o no a
la fórmula de una elipse?
Si corresponden a una elipse, entonces
deberían poder escribirse como:
(iziO!+ (yz2Jl.1
a2
a. Dibujen las siguientes elipses en el mismo sistema de ejes
coordenados:
•. —x + —
y =1
-,
1.
16 4
2 .^ + y i= i
• 25 13
3- i 3 + y2=1
b. Encuentren los focos de cada una de las elipses.
„
b2
Multipliquemos ambos miembros de (i)
por a2b2y calculemos los cuadrados:
b2(x2- 2x x 0+ x 02) + a2(y 2- 2yy 0+ y 02) =
= a2b2
Distribuyendo y agrupando, obtenemos:
b2x 2+ a2y 2- 2xx 0b2- 2yy 0a2+ b2x 02+
+ a2y 02- a 2b2 = 0
En el caso a. debe ser:
• Problema 7
a. Grafiquemos las elipses:
b2 = 4 => b = 2
a2 = 9=>a = 3
-2 x 0b2 = 8 => -2 x 04 = 8 => x 0= -1
- 2y 0a2 = 0 =>y„ = 0
b2x 02+ a2y 02- a2b2 = -32
4 .1 + 9 . 0 - 9 . 4 = -32
Luego, existen a, b.Xj.y,, que verifican
que la ecuación a. es igual a la ecuación
(i).
Con lo cual, la ecuación a. representa
una elipse de centro (-1; 0) con a = 3
y b = 2.
Veamos que pasa con la ecuación b.
b2 = 4 => b = 2
a2 = 9=>a = 3
-2 x 0b2 = l=> -2 x 0.4 = l= > x 0= - - 2y 0a2 = 0 =>y11 = 0
b2x 02+ a2y 02- a2b2 = 3
4- A l + 9- 0 - 9 .4 = -31,9375 # 3
\641
Luego, b. no corresponde a la ecuación
de una elipse.
b. Sabemos que los focos son A = (c; 0 ) y B = (-c; 0),y que
b2= a2- c2, o sea, c2= a2- b2.
En la elipse 1. a2= 16, b2= 4; luego, c = VÍ2
En la elipse 2. a2= 25, b2= 13; luego, c = Vl2
En la elipse 3. a2= 13, b2= 1; luego, c = Vl2
O sea que en las tres elipses los focos son los mismos:
(-V12; 0 )y(V l2 ; 0).
¿Por qué teniendo los mismos focos estas elipses son
diferentes?
Cada elipse es el lugar geométrico de los puntos del plano
tales que la distancia a los focos es 2a, con lo cuál no sólo de­
pende de los focos, sino también del valor de a.
Llamamos excentricidad a la razón entre la distancia entre
los focos y la medida del eje mayor. O sea:
Excentricidad = e = ^ = —
2a
a
93
Como en la elipse c < a, entonces, e < l , y su forma depende
del valor de e.
]_
En la elipse 1., a = 4 y c = V l2 = 2V3
=>e=^V3
En la elipse 2., a = 5 y
=>e=^V3
c
= 2a/3
En la elipse 3., a = VÍ3 y c = 2V3
2
=>e = 2
La circunferencia es una elipse en la cual a = b, pero como
b2= a2- c2, entonces, c = 0 y e = 0.
Conclusión
Las circunferencias son elipses de excentricidad e = 0.
Hasta aquí, vimos lo que ocurre cuando la suma de las distan­
cias a dos puntos fijos resulta constante. Analicemos ahora
qué pasa con la resta de las distancias.
O Problema 8
Dados los puntos A = (50; 0) y B = (-50; 0), encuentren el lugar
geométrico de todos los puntos del plano, tales que la diferen­
cia entre las distancias a A y a B sea de 4 unidades.
• Problema 8
Sea P = (x; y) un punto del plano que verifica la condición
pedida:
|dist(A, P) - dist(B, P)| = 4 (consideramos el módulo dado que
no sabemos cuál de las dos distancias es la mayor).
21. Encuentren, en cada caso, los focos,
la gráfica y la excentricidad de las si­
guientes elipses:
X
4
-A
2
-2
8
-8
|y|
2 4 V Í3
24V13
0
0
24V65
24V65
22. Encuentren dos puntos tales que
el módulo de la diferencia de las distan­
cias a A = (1; 0) y a B = (-1; 0) sea 1.
Realicemos el gráfico que represente la tabla anterior.
Este tipo de curva se llama hipérbola.
x
y1
a. — - ^-=1
4
Hipérbola
Llamamos hipérbola al lugar geométrico de los puntos
del planotalesqueel módulo de la diferencia délas
distancias a dos puntos fijos A y B sea constante.
Los puntos A y B se llaman focos de la hipérbola.
Generalizando este procedimiento, podemos concluir que:
Conclusión
I Si en una hipérbola los focos A y B están sobre el eje x y son
simétricos respecto del origen, sus coordenadas son A = (c; 0) y
B = (-c; 0), con c > 0. Entonces los puntos (x; y) que pertenecen
a la hipérbola verifican la fórmula:
a2
23. Encuentren los focos y la excentrici­
dad de las siguientes hipérbolas
t.
b2
i
donde a es la intersección de la hipérbola con el semieje
positivo de las abscisas (a < c) y b verifica b2= c2- a2.
9
M A T E M A T IC A I LIB R O 4
96
Vectores
CÓNICAS
¿Sabían que...?
El Loran es un sistema que les permite a
los pilotos de avión determinar la posición
de su nave a partir de la diferencia de re­
cepción de las señales de radio, proceden­
tes de dos emisores sincronizados, distan­
tes entre sí. El sistema emisor se compone
de una estación maestra y de otra esclava.
La maestra emite de forma regular una
pequeña señal, que es repetida por la es­
clava, controlada por radio desde la maes­
tra. Ambas señales se reciben en el avión,
se amplifican y se registran como peque­
ñas ondas sobre una pantalla. Los circuitos
del receptor están dispuestos de forma tal
que la distancia entre las señales corres­
ponde a la diferencia de tiempos de llega­
da de las señales de ambas estaciones.
La curva que ve el piloto es, entonces, una
hipérbola.
I Si en una hipérbola los focos A y B están sobre el eje y, sus
coordenadas son A = (0; c) y B =(0; -c) y la ecuación es:
x‘
y2
-a"T - fFr =-1
I Si en una hipérbola los focos A y B están sobre una recta
paralela al eje x, entonces son A = ( x j y j y B = (x2; y j , y la
ecuación es:
(x -x j2
(y —y j 2 , - ( x - x j 2 (y - y 0)2
O ---------- - 5 ------------------------Ü5-------- =
b2
b2
------------------------------------------------- = 1
“ I
donde (x„; y„) es el punto medio entre A y B, x„ = y (x1+ x 2),
y0= y lt la gráfica pasa por el punto (x, + a; y j y c2= a2+ b\
La fórmula es análoga si los focos están sobre una recta
paralela al eje y.
I Las hipérbolas son curvas con excentricidad e = — > 1
Utilicemos la fórmula de la hipérbola con focos sobre un eje
paralelo al ejex, para calcular ( y - y j 2
(x-xj2
(y-yo )2
( x - x 0)2
b2
( x - x ) 2b2 _ b2
( x - x 0)2
( x - x 0)2
a2
_
b2
(x-xj
Con lo cual, a medida que | x -x 0|es cada vez más grande, como
b2
(y-y)2
------------será cada vez más cercano a 0, entonces, — —
( x - x 0)2
(x-x,
se parece cada vez más a —r .
b2
O sea, ( y - y 0)2se aproxima a — (x - x j 2=> |y- y0|se aproxima
3
24. Dada la hipérbola cuya ecuación es:
x
y
25
36
— - — = 1 , encuentren la fórmula de
cada vez más a — (x - x j .
a'
las asíntotas, los focos y el gráfico de la
b
b
Las rectas y - y 0= - (x - x0); y - y 0= - - (x - x0) son
hipérbola.
asíntotas1 de la gráfica de la hipérbola cuya fórmula es:
(x -x „ )2
a2
( y - y 0)2
b2 "
Si, en cambio, tomamos la hipérbola con focos sobre el eje y,
las asíntotas serán:
y - y » = b (x - x °)
y - y » = - ü ( x - xo)
Veámoslo gráficamente:
25. Encuentren gráfica y analíticamen­
te, si existen, el o los puntos que estén
en la intersección de las siguientes
hipérbolas:
O Problema 9
En el comedor de su casa, Ariel tiene un sillón en el cual se
sienta a leery una obra de arte colgada en la pared. Compró
una lámpara de pie y desea ubicarla a igual distancia del
sillón que de la pared, para poder leer sin problemas y para
que se luzca su cuadro. ¿En qué lugares puede colocar Ariel la
lámpara?
1Ver Libro 2, capítulo 2.
5
6
5
9
M A T E M A T IC A I LIB R O 4
98
Vectores
CÓNICAS
26. Decidan cuáles de las siguientes
fórmulas pueden representar una
hipérbola; para las que sea posible,
encontrar los focos,
a. 5x2+ 20x - 4y2+ 24y -3 6 = 0
• Problema 9
Para analizar dónde debe poner Ariel la lámpara, veamos la
situación en un sistema de ejes coordenados.
Representemos la pared como una recta vertical y el sillón,
como un punto sobre el eje x. Ubicamos al eje y en el punto
medio entre la pared y el sillón.
L: x = -c
tí
O h
F (silló n )
o
b. 5x2+ 20x- 4y2+ 2 4 y -6 = 0
Queremos encontrar un punto P = (x,-y) cuya distancia a la
recta L sea la misma que al punto F.
O sea: dist(P, L) = dist(P, F)
Como la recta es vertical, la distancia de P a L es |x + c| =>
=> |x + c| = V ( x - c ) 2+y2
Si elevamos al cuadrado ambos miembros:
2xc +
2xc +
y2
c. x 2+ 5 = 2y2- 3
Cancelando obtenemos: x=
Si graficamos, vemos que puede ubicar la lámpara en:
d
t©
99
Parábola
Llamamos parábola al lugar geométrico de los puntos
del plano que equidistan de un punto F, llamado foco, y
de una recta, llamada directriz.
Si la recta directriz es horizontal, su ecuación es y = -c,
con c e IR, y el foco es F = (0; c), con lo cual, la ecuación de la
parábola resulta:
y=
X2
que es la fórmula de una función cuadrática.
Conclusión
¿Sabían que...?
Cuando hacemos girar una parábola alre­
dedor de su eje, se obtiene una superficie
parabólica.
Estas superficies son las únicas que cum­
plen con una propiedad llamada "reflec­
tora”, que dice que al situar un punto lu­
minoso en el foco, los rayos se proyectan
paralelos al ejey, recíprocamente, los ra­
yos que inciden perpendicularmente a la
directriz se concentran en el foco.
Esta propiedad es la que hace que las an­
tenas, los proyectores y los radares tengan
forma parabólica.
Analicemos el funcionamiento de las ante­
nas de televisión satelital.
La ecuación de la parábola de foco F = (c; 0) y directriz x = -c
y2
es x = 4 c’
La ecuación de la parábola de foco F = (0; c) y directriz y = -c
x2
esy=
Sus respectivas gráficas son:
El satélite emite ondas, todas paralelas en­
tre sí, que al rebotar en la antena conver­
gen al foco y, desde allí, llegan al televisor
por cable.
Esta misma propiedad es la que se utiliza
para los micrófonos de ambiente, para los
telescopios y para los faros de los autos.
27. Encuentren la fórmula de la
parábola que tenga directriz x = -4
y foco F = (4; 0).
28. Encuentren la fórmula de la
parábola que tenga directriz y = -8
y foco F = (0; 8).
29. Encuentren el foco y la directriz de
las siguientes parábolas:
a. x 2 = 6y
Secciones cónicas
O Problema 10
Apolonio de Praga, “el gran geómetra", fue el que introdujo los
términos cónicas, hipérbola y parábola.
En su libro Secciones cónicas, mostró que al cortar un cono con
distintos planos se obtienen las diferentes curvas cónicas.
Los dibujos que realizó fueron los siguientes:
11
1 1 :
T t
*
4
¿Oué curva cónica obtuvo en cada caso?
• Problema 10
Como vemos, en el primer dibujo, obtuvo circunferencias al
cortar el cono con un plano. En el segundo, obtuvo elipses;
en el tercero, hipérbolas, y en el cuarto, parábolas.
Los últimos tres dibujos son casos especiales. En el primero,
queda un punto; en el segundo, una recta y en el tercero, dos
rectas. Por esta razón es que Apolonio llamó a estas curvas
secciones cónicas.
Llamamos secciones cónicas a las curvas que se obtienen
como intersección de un cono con un plano.
GE 4
GUÍA DE EJERCITACIÓN
1. Encuentren la ecuación de la circunferencia de centro (0; 2) y radio 3.
O
2. Encuentren gráfica y analíticamente, si existe, la intersección entre la circunferencia del
ejercicio 1. y la de centro (2; 0) y radio 3.
O
o
3. Encuentren la ecuación de una circunferencia que verifique que el segmento cuyos
extremos son (10; -5 )y (7; 3) sea un diámetro.
4. ¿Cuáles de las siguientes fórmulas representan la ecuación de una circunferencia?
a. x2+ y2+ 5x + y = 3x - 2y - 5
o
b. x2+ y2+ 4y = x +1 - xy
c. x2+ 2y2- 8x + y = - x2+ y - 6
O
GE 4
Vectores
Cónicas
GUÍA DE EJERCITACIÓN
5. a. ¿Cuántas circunferencias que pasan por (1; 2) y (3; -1) pueden encontrar?
O
b. Encuentren la que, además, pasa por (0; 4).
O
6. Dada la circunferencia de ecuación x 2+ 4x = - y 2-2y:
a. Encuentren cinco puntos que estén dentro de la circunferencia.
b. Encuentren cinco puntos que estén fuera de la circunferencia.
O
c. Encuentren cinco puntos que estén sobre la circunferencia.
O
7. Calculen la ecuación de la elipse formada por los puntos cuya suma de las distancias a los
puntos A = (3; -5) y B = (3; 5) sea 15.
O
__________________
1
ALUM NO
-1
CURSO
-1
FECH A
GE 4
GUÍA DE EJERCITACIÓN
8. Dadas las siguientes gráficas, determinen las fórmulas de las curvas que representan:
O
O
o
o
o
■
1
ü
GE 4
GUIA DE EJERCITACION
1
Vectores
Cónicas
9. Encuentren gráfica y analíticamente una elipse de centro (1; 9) y que pasa por (1; 20) y
por (13; 9)..
10. ¿Cuáles de las siguientes ecuaciones representan una elipse? ¿Por qué?
a. x2+ 2y2= -2 x + 12y -1 7
b. x2+ y2+ 6y = 8
O
O
11. Encuentren gráfica y analíticamente las intersecciones de las siguientes elipses:
O
9x2+ 25y2- 54x - 200y + 256 = 0
o
12. Dada la elipse de ecuación: 9x2+ 4y2- 90x + 16y + 205 ¡
a. Encuentren 5 puntos que estén dentro de la elipse.
b. Encuentren 5 puntos que estén fuera de la elipse.
O
ALU M N O
CURSO
FECH A
GE 4
GUÍA DE EJERCITACIÓN
c. Encuentren 5 puntos que estén sobre la elipse.
O
13. Determinen qué fórmula corresponde a cada gráfico.
a-
O
x2 y2 .
4 + 25
u x
y
-,
b‘ 2 ^ + 4 =1
x
4
y
4
,
C. -7- + ^ = 1
d . ?9 + £25 - l
O
14. Encuentren la ecuación y la gráfica de la hipérbola formada por los puntos cuya resta
de distancias a los puntos A = (3; 0) y B = (-3; 0) sea 5.
O
15. Encuentren gráfica y analíticamente los puntos que estén en la intersección de las
siguientes curvas:
(x-3)2+ - ^ ^ = l
a.
(x - B ) 2- i y ^ = i
o
■
ALUM N O
1CURSO
1
GE 4
Vectores
Cónicas
GUIA DE EJERCITACION
x2- y 2= 4
b.
16
O
9
O
16. Encuentren en cada caso la ecuación de la parábola que tiene:
a. Foco (1; 0) y directriz x = -1
O
b. Foco (0; -1) y directriz x = 1
____________________________________________________________________________
O
17. Encuentren el foco y la directriz de las siguientes parábolas:
a-y = y x
b .x2- | y - 0
O
ALU M N O
CURSO
FECH A
GA 4
GUÍA DE AUTOEVALUACIÓN
1. Decidir qué gráfica corresponde a cada fórmula:
O
b. 4x2- 40x - y2+ 2y+ 95 = 0
c. 2y2- 5x = 0
d. 5x2+ 5y2-45 = 0
O
2. Graficar las curvas que representan las siguientes ecuaciones:
a. 16x2- 25y2= 160x - 50y + 25
o
b. 16x2+ 25y2= 160x + 50y - 25
o
c. x2+ y 2= lOx + 2y + 374
d. 4y2- lO x = 0
O
■
ALUMNO
■
■
1
GA 4
GUIA DE AUTOEVALUACION
H
I
Vectores
Cónicas
3. Encontrar gráfica y analíticamente los puntos de intersección entre las siguientes curvas:
x 2- 2x + y 2- 6y + 2 = 0
( x - l) 2 , (y-3)2 .
O
x2+ y2- 4 x - 8 y = -19
(x-2)2
( y -4 ) 2 _ 1
O
4. ¿La parábola de directriz x = -4 yfo co F = (4; 0) corresponde a una función? ¿Porqué?
-----------------------------------------------------------------------------------------------------
5. De una curva se sabe que la distancia entre sus focos es 10 cm y el eje mayor mide 24 cm.
¿De qué curva se trata? ¿Por qué?
6. De una curva se sabe que la distancia entre sus focos es 10 cm y el eje mayor mide 6 cm.
¿De qué curva se trata? ¿Por qué?
ALU M N O
CURSO
FECH A
O
109
Respuestas
Guías de autoevaluación
Capítulo 1
1 . V + W ; U + W ; - V;
-2
4. (2; 3); (1; -2); (9; 27); -13.
V; - W .
3
5.m
0
2 . a.
y
y
AUfd
b. (4; 3)
c. (2V2; 315“
6. Hay dos vectores que cumplen
> -H
las condiciones pedidas:
O
(-3,317;-3,74102)
y (-1,0024; 4,885)
7. Solución única: x = 3.
3. m = 1
Capítulo 2
2. a. (-2; -3 ; 2)
1.a. ÁB = (-3; - 6; 5)
b. (30; 0; -10)
BD = (0; 3 ;- 8)
CA = (3;-6; 5)
C. (8 ;
DC = (6; 6;-2 )
|BD|=V73
g.
|DC| =V76
» 1 1
4 ; - ; - -
...
b.D = (4;2,-5)
4. Una solución es: (2; 1; 0).
No es única.
16 101 15 : 15
e. -11
|CA| =V70
а.D=
9;-10)
»1 3
' E 15 :
b. |ÁB| = V7Ü
V l4
f . -7
(1; —2; —1)
h. (0; —10; 0)
б. m = 4 2
Tres puntos pueden ser: (0; 6; 2), (3; 15; 4) y (-3; -3 ; 0).
Capítulo 3
1. a. 6
3. Por ejemplo:
b. —
4
c. - 4
b. L: X = k(2; 9; -10) + (2; -3 ; 7), k e IR
Tres puntos pueden ser: (2; -3 ; 7), (4; 6; -3 ) y (0; -12; 17).
d. no existe
C.
e. y = -2 ; z = —
f. -9
2
L: X
=
k(2;-2
; - 2 “',k£lR
\ , ;, 5)l + I 2 ’ -3’
»3
5
Tres puntos pueden ser: ¿ " 2 ’ 3 '
2. L: X = k(-5; 3) + (-5 ; -7), k e IR
4 .y = 1
3. a. L: X = k(3; 9; 2) + (0; 6; 2), k e IR
5. L: X = k (0; 1; 0) + (0; 2; -2), k E IR
6. (0; 1; - 2)
7. L: X = k (0; -1 ; 1) + (2; -3 ; 0), k e IR
~ »i
i
... »5
7
’ i 2 : _ 3 ;3 y * 2 ; _ 3 ;
'
M A T E M Á T IC A | LIBRO 4
110
Vectores
Respuestas
Guías de autoevaluación
Capítulo 4
l.a .I
b. II
c. IV
d. III
15
1 + - V5; 3+ - V5 , 1 + 1 V 5 ; 3 - | VsJ, | l - | V5;3+| V5| y | l - | V 5 ; 3 - | V 5
5
5 /
b.
O
N
/
S
\
/
/
/
/
/
1
No hay puntos de intersección entre estas curvas.
v
4. No corresponde a una función dado que para un mismo valor de x hay dos valores de y.
5. Se trata de una elipse dado que la excentricidad es menor que 1 (a = 6 y c = 5).
6. Se trata de una hipérbola dado que la excentricidad es mayor que 1 (a = 6 y c = 3).
©
111
Notas
112
Notas
113
Notas
Esta edición se term inó
de im prim ir en los talleres de Longseller,
Buenos Aires, Argentina,
en el mes de febrero de 2002.
Matemàtica
Vectores
Silvia V.AItman |Claudia R. Comparatore |Liliana E. Kurzrok
Libro i
Funciones
Libro 5
Análisis 7
j
Libro 2
Funciones 2
Libro 6
Análisis 2
Libro 3
Números y sucesiones
Libro 8
Probabilidad y estadística
<Q> longseller
Código interno: 1924
ISBN 987-550-041-0
Libro 4
Vectores






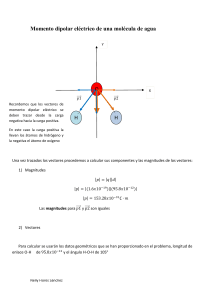


![1 Si v = [ 36 -12 ] , w = [ 9 -3 ] , y S = 1wl. Indique cuáles opciones](http://s2.studylib.es/store/data/004950498_1-7f0b4c506a631255d680bd90dfa0a3e5-300x300.png)