rectas y producto escalar
Anuncio
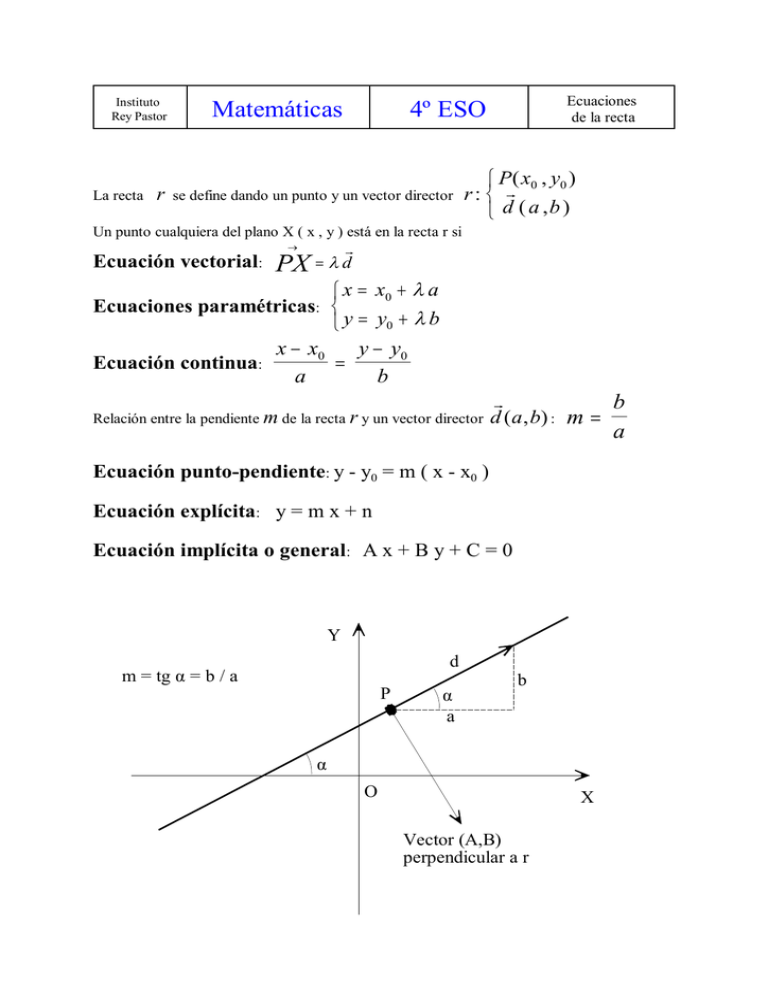
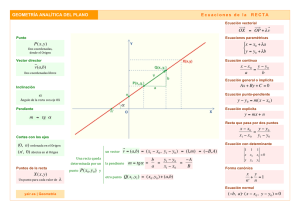
Instituto Rey Pastor La recta r Matemáticas Ecuaciones de la recta 4º ESO se define dando un punto y un vector director P ( x0 , y0 ) r: d ( a ,b ) Un punto cualquiera del plano X ( x , y ) está en la recta r si Ecuación vectorial: PX d x x0 a Ecuaciones paramétricas: y y0 b x x0 y y0 Ecuación continua: a b Relación entre la pendiente m de la recta r y un vector director b d ( a , b) : m a Ecuación punto-pendiente: y - y0 = m ( x - x0 ) Ecuación explícita: y = m x + n Ecuación implícita o general: A x + B y + C = 0 Y d m = tg α = b / a P α a b α O X Vector (A,B) perpendicular a r Instituto Rey Pastor Matemáticas Dados los vectores u ( x1 , y1 ) y 4º ESO B Producto escalar v ( x2 , y2 ) Módulo de un vector = u x12 y12 Definición de producto escalar: u . v u . v .cos Cálculo del producto escalar: u . v x1 . x2 y1 . y2 Perpendicularidad: u v 90º cos 0 u . v 0 Si u ( a , b) entonces v (b , a ) es perpendicular a u porque u . v a .b b .( a ) a .b b . a 0 Ángulo entre dos vectores: cos u .v u .v