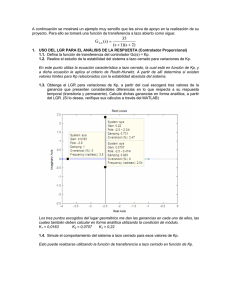
CÉSAR AUGUSTO AVILA LAITÓN INGENIERÍA ELECTROMECÁNICA UNIVERSIDAD AUTÓNOMA DE COLOMBIA SISTEMAS DINÁMICOS Diseño de un controlador PID Se desea diseñar un controlador PID tal que los polos dominantes cumplan con los siguientes requisitos: Ov=16% y tss=2s. La FT del sistema es la siguiente: 𝐺(𝑠) = 10 𝑠 2 + 10 Los polos de G(s) son [√2𝑗 − √2𝑗]. Luego hay que encontrar el LGR, para facilitar el proceso se usa Matlab, el código y el LGR son los siguientes: 1. Hay que encontrar el polinomio deseado para ubicarlo en el LGR: 𝑃𝐷 = −𝜀𝜔𝑛 ± √1 − 𝜀 2 𝜀=− ln(0,12) √𝜋 2 + ln2 (0,12) 𝜔𝑛 = 4 2(0,56) = 0,56 = 3,57𝑟𝑎𝑑/𝑠 𝑃𝐷 = −(0,56)3,57 ± 𝑗3,57√1 − (0,56)2 𝑃𝐷 = −2 ± 2,96𝑗 2. Debe cumplir la condición de fase °𝐺(𝑠) = ±180°. °𝐺(𝑠) = ∑ °𝑐𝑒𝑟𝑜𝑠 − °𝑝𝑜𝑙𝑜𝑠 = 0 2 𝜃 = 𝑡𝑎𝑛−1 ( ) = 34° 2,96 2 𝛽 = 𝑡𝑎𝑛−1 ( ) = 24° 2,96 + √2 2 𝛼 = 𝑡𝑎𝑛−1 ( ) = 52° 2,96 − √2 °𝐺(𝑠) = 0 − (142 + 114 + 124) = −380° Para que esta condición se cumpla: 200 − 380 = −180° 𝑋1+ 𝑋2 = 200° Para facilitar el procedimiento 𝑍𝑐2 = 0 así, el grado con respecto a P.D es igual a 124°. 124 + 76 = 200° 𝑋1 = 2,96 = 0,738 𝑡𝑎𝑛76 °𝐺(𝑠) = (124 + 76) − (142 + 114 + 124) = −180° 𝑍𝑐1 = −2,738 3. Condición de magnitud: 𝐾|𝐶𝐺(𝑠)| = 1 Ahora hay que hallar la magnitud de cada uno de los polo y ceros hacia el P.D: 𝐴 = √22 + (2,96 − √2)2 = 2,53 𝐵⁄𝐶 = √22 + (2,96)2 = 3,57 𝐷 = √22 + (2,96 + √2)2 = 4,8 𝐸 = √𝑂, 7382 + (2,96)2 = 3,05 Entonces: 𝐾 (10) ∗ 𝐶 ∗ 𝐸 =1 𝐴∗𝐵∗𝐷 𝑘 = 0,398 La C(s) del controlador PID es: 𝐶(𝑠) = 0,398 (𝑠) (𝑠 + 2,738) 𝑠 La simulación es Simulink es la siguiente: Para comprobar de una manera más precisa que el diseño del controlador PID cumple con los requisitos, hallamos el LGR del sistema con el controlador en Matlab. El código es el siguiente: El LGR es: Como se observa en las características del LGR, se llegan a valores muy aproximados a los requisitos establecidos, es decir el diseño del controlador PID cumple con el diseño.