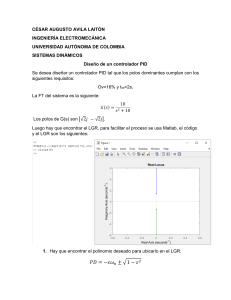
2) 1)(s (s 35 (s) + +

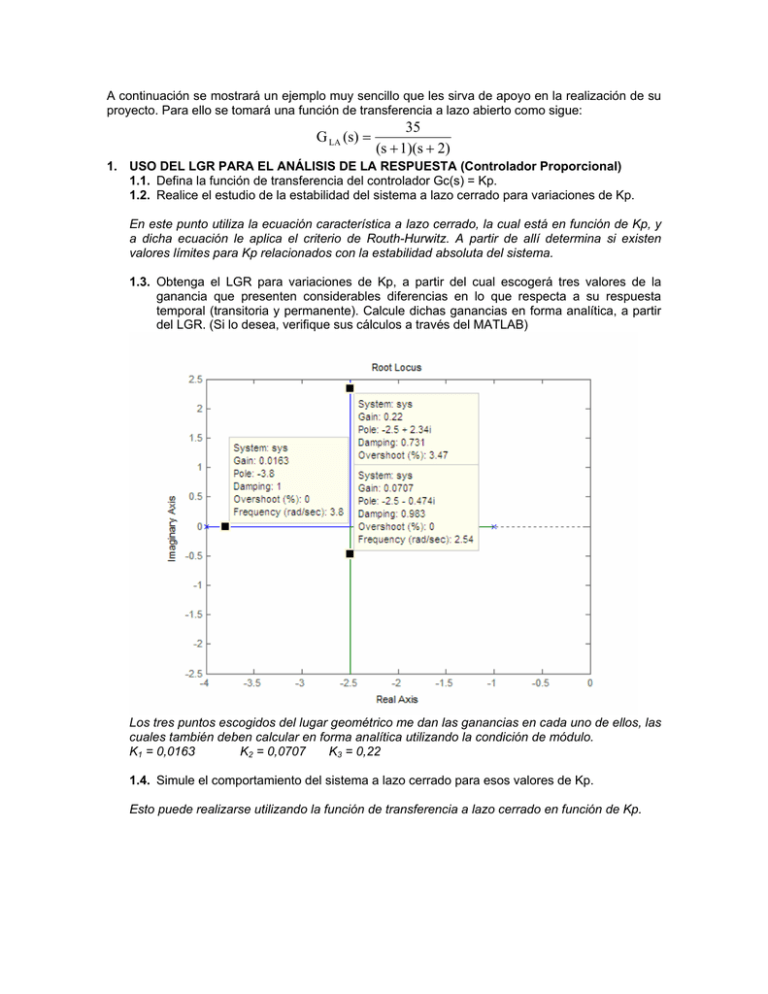
A continuación se mostrará un ejemplo muy sencillo que les sirva de apoyo en la realización de su
proyecto. Para ello se tomará una función de transferencia a lazo abierto como sigue:
G LA (s) =
35
(s + 1)(s + 2)
1. USO DEL LGR PARA EL ANÁLISIS DE LA RESPUESTA (Controlador Proporcional)
1.1. Defina la función de transferencia del controlador Gc(s) = Kp.
1.2. Realice el estudio de la estabilidad del sistema a lazo cerrado para variaciones de Kp.
En este punto utiliza la ecuación característica a lazo cerrado, la cual está en función de Kp, y
a dicha ecuación le aplica el criterio de Routh-Hurwitz. A partir de allí determina si existen
valores límites para Kp relacionados con la estabilidad absoluta del sistema.
1.3. Obtenga el LGR para variaciones de Kp, a partir del cual escogerá tres valores de la
ganancia que presenten considerables diferencias en lo que respecta a su respuesta
temporal (transitoria y permanente). Calcule dichas ganancias en forma analítica, a partir
del LGR. (Si lo desea, verifique sus cálculos a través del MATLAB)
Los tres puntos escogidos del lugar geométrico me dan las ganancias en cada uno de ellos, las
cuales también deben calcular en forma analítica utilizando la condición de módulo.
K1 = 0,0163
K2 = 0,0707
K3 = 0,22
1.4. Simule el comportamiento del sistema a lazo cerrado para esos valores de Kp.
Esto puede realizarse utilizando la función de transferencia a lazo cerrado en función de Kp.
A partir de estas simulaciones (verde (k1), Azul (K2) y rojo (k3), se deben obtener los valores
relativos a las respuestas transitorias y permanentes (constantes de tiempo, Mp, tp, error, etc)
Lo cual dbe ser verificado teóricamente a partir de la función de transferencia a lazo cerrado
para cada valor de Kp. Punto 1.5
Analice la respuesta temporal obtenida, tanto en su parte transitoria como permanente.
1.5. Dicho análisis se debe fundamentar en lo obtenido vía simulación y en estudios teóricos
de la respuesta (análisis de los polos del sistema y del error).
1.6. Recuerde que debe escoger valores de Kp que modifiquen apreciablemente la respuesta.
Esto es factible siempre que se escojan raíces a lazo cerrado a partir del LGR que
presenten variaciones importantes.
2. USO DEL LGR PARA EL ANÁLISIS DE LA RESPUESTA (Controlador PD)
2.1. Defina la función de transferencia del controlador Gc(s) = Kp (Td s + 1).
2.2. Fije el valor de Kp, tomando alguno de los estudiados en el punto 1, tal que sea
importante la adición de la parte derivativa al controlador, es decir, escoja la peor de las
respuestas transitorias.
2.3. Realice el estudio de la estabilidad del sistema a lazo cerrado para variaciones de Td.
2.4. Obtenga el LGR para variaciones de Td, a partir del cual escogerá tres valores del tiempo
derivativo que presenten considerables diferencias en lo que respecta a su respuesta
temporal (transitoria y permanente). Calcule dichos valores en forma analítica, a partir del
LGR. (Si lo desea, verifique sus cálculos a través del MATLAB)
En este caso, al igual que en el PI, se realiza lo mismo que en el punto anterior, pero lo primero
que se debe realizar es manipular la ECLC tal que esté descrita en la forma necesaria para la
obtención del LGR para variaciones de Td. Para el ejemplo en particular tendríamos lo
siguiente.
Tomando la mayor de las ganancias K = 0.22 se tendrá una ECLC como la que sigue:
1+
0.22(1 + tds )
=0
( s + 1)( s + 4)
s 2 + 5s + 4.22 + 0.22tds
=0
s 2 + 5s + 4.22
s
1 + 0.22td 2
=0
s + 5s + 4.22
De esta forma, es posible realizar el LGR para variaciones de Td y repetir un procedimiento
parecido al anteriormente mencionado. Para el caso del PI se realizaría los mismo.