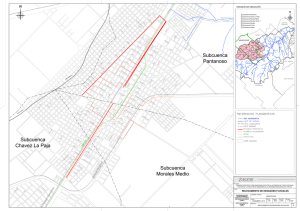
Análisis de la Respuesta a Lazo Cerrado

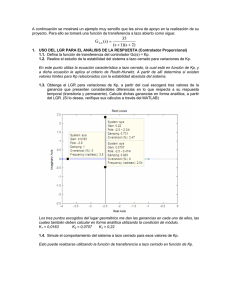
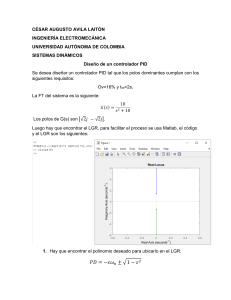
PROYECTO #2 (5%)
FECHA DE ENTREGA: SEGUNDO PARCIAL
CONTROL DE PROCESOS I(PS2319)
Análisis de la Respuesta a Lazo Cerrado
El objetivo de esta asignación es analizar la respuesta a lazo cerrado de un sistema y comprender la acción
que los diferentes tipos de controlador pueden tener sobre la respuesta de un esquema de control de
retroalimentación simple, como el mostrado en la siguiente figura.
Para ello, se utilizará el LGR como herramienta de análisis de la respuesta transitoria a lazo cerrado, en tanto
que la respuesta permanente se estudiará en función al error en estado estacionario. Para realizar lo anterior
debe utilizar un juego de parámetros específicos en la función de transferencia del proceso estudiado por
usted en la primera parte del proyecto, es decir, fije los parámetros del proceso, no los cambie más y realice
lo siguiente.
1. USO DEL LGR PARA EL ANÁLISIS DE LA RESPUESTA (Controlador Proporcional)
1.1. Defina la función de transferencia del controlador Gc(s) = Kp.
1.2. Realice el estudio de la estabilidad del sistema a lazo cerrado para variaciones de Kp.
1.3. Obtenga el LGR para variaciones de Kp, a partir del cual escogerá tres valores de la ganancia que
presenten considerables diferencias en lo que respecta a su respuesta temporal (transitoria y
permanente). Calcule dichas ganancias en forma analítica, a partir del LGR. (Si lo desea, verifique
sus cálculos a través del MATLAB)
1.4. Simule el comportamiento del sistema a lazo cerrado para esos valores de Kp.
1.5. Analice la respuesta temporal obtenida, tanto en su parte transitoria como permanente.
1.6. Dicho análisis se debe fundamentar en lo obtenido vía simulación y en estudios teóricos de la
respuesta (análisis de los polos del sistema y del error).
1.7. Recuerde que debe escoger valores de Kp que modifiquen apreciablemente la respuesta.
2. USO DEL LGR PARA EL ANÁLISIS DE LA RESPUESTA (Controlador PD)
2.1. Defina la función de transferencia del controlador Gc(s) = Kp (Td s + 1).
2.2. Fije el valor de Kp, tomando alguno de los estudiados en el punto 1, tal que sea importante la adición
de la parte derivativa al controlador, es decir, escoja la peor de las respuestas transitorias.
2.3. Realice el estudio de la estabilidad del sistema a lazo cerrado para variaciones de Td.
2.4. Obtenga el LGR para variaciones de Td, a partir del cual escogerá tres valores del tiempo derivativo
que presenten considerables diferencias en lo que respecta a su respuesta temporal (transitoria y
permanente). Calcule dichos valores en forma analítica, a partir del LGR. (Si lo desea, verifique sus
cálculos a través del MATLAB)
2.5. Simule el comportamiento del sistema a lazo cerrado para esos valores de Td.
2.6. Analice la respuesta temporal obtenida, tanto en su parte transitoria como permanente.
2.7. Dicho análisis se debe fundamentar en lo obtenido vía simulación y en estudios teóricos de la
respuesta (análisis de los polos del sistema y del error).
2.8. Recuerde que debe escoger valores de Td que modifiquen apreciablemente la respuesta.
3. USO DEL LGR PARA EL ANÁLISIS DE LA RESPUESTA (Controlador PI)
3.1. Defina la función de transferencia del controlador Gc(s) = Kp (1 + 1/Ti s).
3.2. Fije el valor de Kp, tomando alguno de los estudiados en el punto 1, tal que sea importante la adición
de la parte integral al controlador.
3.3. Realice el estudio de la estabilidad del sistema a lazo cerrado para variaciones de Ti.
3.4. Obtenga el LGR para variaciones de Ti, a partir del cual escogerá tres valores del tiempo integral
que presenten considerables diferencias en lo que respecta a su respuesta temporal (transitoria y
permanente). Calcule dichos valores en forma analítica, a partir del LGR. (Si lo desea, verifique sus
cálculos a través del MATLAB)
3.5. Simule el comportamiento del sistema a lazo cerrado para esos valores de Ti.
3.6. Analice la respuesta temporal obtenida, tanto en su parte transitoria como permanente.
3.7. Dicho análisis se debe fundamentar en lo obtenido vía simulación y en estudios teóricos de la
respuesta (análisis de los polos del sistema y del error).
PROYECTO #2 (5%)
FECHA DE ENTREGA: SEGUNDO PARCIAL
CONTROL DE PROCESOS I(PS2319)
Nota 1: En cada uno de los puntos anteriores, si la escala lo permite, las simulaciones deberán realizarse en
una sola gráfica. Se espera un análisis teórico que incluya el cálculo del τ, (si su aproximación es a primer
Orden), ζ y ωn (si su aproximación es a segundo orden subamortiguado), ts, valor de establecimiento y error,
así como, su comparación con lo simulado.
Nota 2: La estructura del informe forma parte de la evaluación. La entrega deberá ser tanto en papel como
digital (diskette anexo o enviada por correo electrónico), de lo contrario no será considerada como completa.