Desigualdades

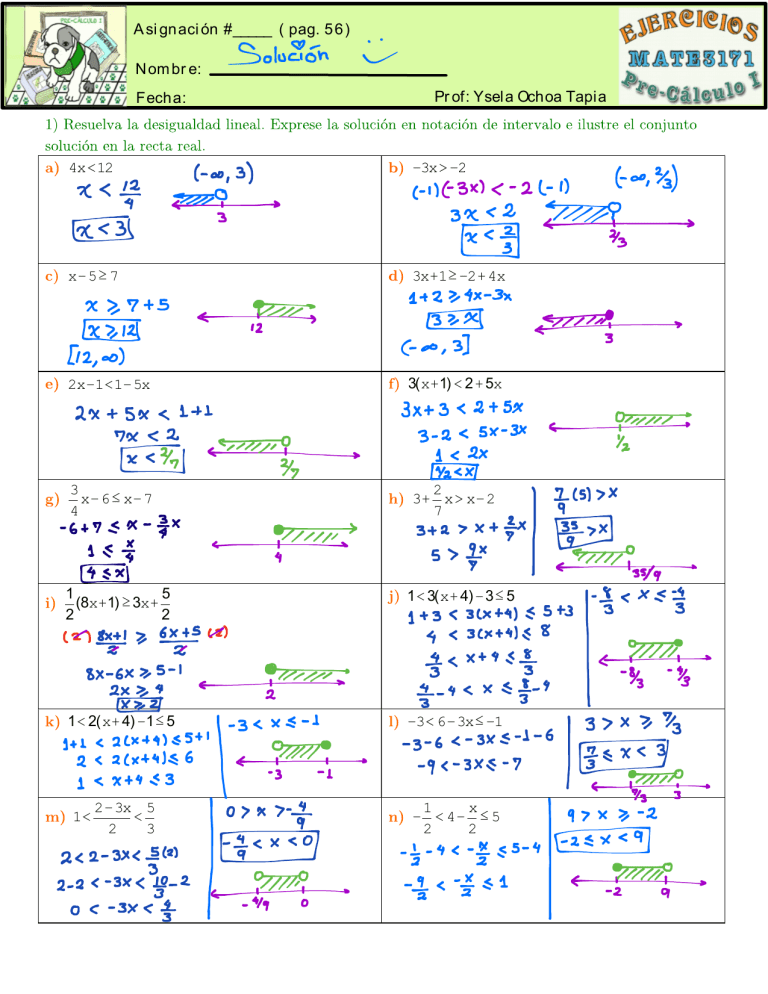
A si gn aci ón #_____ ( pag. 5 6 )
N om br e:
Fecha:
Pr of: Ysela Ochoa Tapia
4x<12
−3x> −2
x− 5≥ 7
3x+1≥ −2+ 4x
2x−1<1− 5x
3(x+1) < 2+ 5x
3
x− 6 ≤ x− 7
4
2
3+ x> x− 2
7
1
5
(8x+1) ≥ 3x+
2
2
1< 3(x+ 4) −3≤ 5
1< 2(x+ 4) −1≤ 5
−3< 6−3x≤ −1
2−3x 5
<
2
3
1
x
− < 4− ≤ 5
2
2
1<
x2 −3x−10< 0
x2 + x>12
2x2 < 5x+3
4x9 + 9 ≥ 6x
2(2x2 −3x) ≥ −9
x3 +8x2 < 0
x3 + 2x2 −3x> 0
x4 > x
x4 > x2
x−3
≥0
x+1
Ojo: Hay multi pli ci dad en x=0 es por el lo que
dupl i co l os si gnos.
(x−1)(x+1)
<0
x
x−1
≥0
x2 − 4
N ota: Los ej ercici os m y r presentan multipl i cidad y ti ene una l i gera modi fi cación para encontrar l a sol uci ón por el segundo
metodo del cemeteri o. (Para evitar esto, se debe trabaj ar con el pri mer método del cementeri o, es deci r, dando val ores)
(x+ 5)2
≤0
x2 − 4
x+ 2
≥1
x− 4
3x−5
≤2
x+2
1
2
<
x− 2 3x−9
x(x2 +1)(x− 2)
≥0
(x−1)(x+1)
2+
1
1
<
x−1 x+1
Oj o: H ay mul ti pl ici dad en
x=0 es por ell o que dupl ico
l os si gnos
x−1 ≤ 2
1−2x > 3
2−3x >1
3(x−1) +2 ≤ 20