Caída de Tensión - Análisis Vectorial

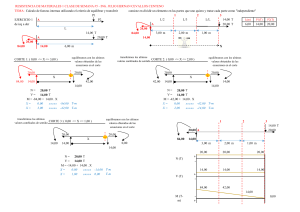
Caída de Tensión – análisis vectorial
Ing. Pablo Daubian – [email protected]
En términos vectoriales:

U

 
 
U0  Uf
I Z

U

 
  


U0  Uf
I ( R  j X)
Podemos escribir a R y X como…

R

L  R km

X

L  X km
Quedando…
 
 

U
I L  Rkm  Xkm
Aquí podemos hacer una simplificación, debido a que en general la caída de
tensión es pequeña, en lugar de trabajar con las magnitudes vectoriales,
podemos tomar las proyecciones de las caídas por resistencia y reactancia sobre
el vector Uf, obteniendo…
U

I L  Rkm cos (  )  Xkm sen (  ) 
La ventaja de la expresión anterior es evidente, solo debemos operar
algebraicamente con magnitudes escalares.
También podemos escribir…
U

U  I L  Rkm cos (  )  Xkm sen (  ) 
U
Pero
U I
S
quedando

S L  Rkm cos (  )  Xkm sen (  ) 
U
U
Resumiendo, obtenemos…
Tensión monofásica
U

U

2  I L  Rkm cos (  )  Xkm sen (  ) 
2  S L  Rkm cos (  )  Xkm sen (  ) 
U
U%

U
U
 100 %
U
220 V

Tensión trifásica
U


U
3 I L  Rkmcos (  )  Xkm sen(  ) 
S L  Rkm cos (  )  Xkm sen (  ) 
U

U
 100 %
U
380  V

U%
U