Tema-6-Funciones

MATEMÁTICAS Mayores de 25 años
Tema 6. Funciones.
Función real: dominio y recorrido. Funciones elementales.
Operaciones y propiedades de funciones: simetrías, funciones pares e impares.
Periodicidad. Acotación. Monotonía. Máximos y mínimos absolutos y relativos.
Estudio y representación de funciones elementales.
Sucesiones: idea intuitiva de límite.
Cálculo de límites sencillos de sucesiones: indeterminaciones.
Idea intuitiva de límite de funciones.
Límites infinitos y en el infinito: asíntotas verticales, horizontales y oblicuas.
Concepto de continuidad de una función: discontinuidades.
IPEP de Granada
Dpto. de Matemáticas
Tema 6. Funciones.
Función real: dominio y recorrido.
Do mi ni o d e u na fu n ci ó n
http://www.vitutor.com/fun/2/a_2.html
El do mi ni o e s el co nj u n to d e e le me n to s q u e ti en e n i mag e n .
C onjunto inic ia l
D om inio
C onjunto fina l
C onjunto im a ge n o re c or r ido
En tanto que, llamaremos recorrido de f al conjunto de valores que toma la variable dependiente, y.
Lo denotaremos R(f).
En el ejemplo de la piscina 2, D(f)=[0, 5] y R(f)=[0,125].
E s tudio de l dom inio de una func ión
D om inio de la func ión polinóm ic a e nte r a
El do mi ni o e s R , cua l q ui e r n ú me ro re a l ti e ne ima g en .
Ej e mp lo
f(x)= x 2 - 5 x + 6
D =R
http://www.vadenumeros.es/primero/dominio-y-recorrido-de-funciones.htm
Son funciones polinómicas las rectas, las funciones cuadráticas (parábolas) y las funciones
polinómicas de grado superior
Ejemplos
D om inio de la func ión ra c iona l
El d o mi n i o e s R me n o s lo s va l o re s qu e an u la n al d en o mi na d o r (n o pu e d e e xi sti r
un nú me ro cu yo de n o mi n a do r sea ce ro ).
Ej e mp lo
Ejemplos
D om inio de la func ión irr a c iona l de índic e im pa r
El do mi ni o e s R .
Ej e mp lo s
1.
2.
D om inio de la func ión irr a c iona l de índic e pa r
El do mi ni o e stá fo rma d o p o r to d o s l os va l o re s q ue ha ce n qu e el ra di ca n do sea
ma yo r o ig u al qu e ce ro .
Ej e mp lo s
1.
2.
3.
4.
Ejemplos
D om inio de la func ión loga r ítm ic a
El do mi ni o e stá fo rma d o p o r to d o s l os va l o re s q ue ha ce n qu e el l a fu n ció n
con te n i da de n tro d el lo g a ri tmo sea ma yo r q u e ce ro .
Ej e mp lo
Ejemplos
Definición de logaritmo
Siendo a la base, x el número e y el logaritmo.
Funciones elementales.
Func ión line a l y a fín
Las funciones polinómicas de primer grado, también llamadas funciones afines son aquellas cuya
ecuación es del tipo f(x) = mx + n
Algunas de sus características principales son:
Su dominio es todo
Si m > 0, la función es creciente
Su gráfica es una recta con pendiente m
Si m < 0, la función es decreciente
Pasa por el punto (0,n) [Punto de corte con el eje OY]
Dentro de las funciones afines podemos distinguir dos tipos. En una función afín: f(x) = mx + n
· Si m = 0, la función y = n se denomina función constante. Su gráfica es una recta paralela al eje
OX, que pasa por el punto (0,n)
· Si n = 0, la función y = mx se denomina función lineal y su gráfica es una recta de pendiente m que
pasa por el origen de coordenadas (0,0)
Ej e mp lo
y = 2x
x
0
1
2
3
4
y = 2x
0
2
4
6
8
Func ión ide ntida d
f(x) = x
S u g rá fi ca e s l a
cua d ra n te .
b i se ctri z
d el
p ri me r
y
te rce r
Funciones cuadráticas
Las funciones polinómicas de segundo grado, también llamadas funciones cuadráticas son aquellas cuya
ecuación es del tipo:
f(x) = ax2 + bx + c
con
.
Algunas de sus características principales son:
Su dominio es todo
El vértice de la parábola es
Su gráfica es una parábola, simétrica respecto a eje de simetría que Cuanto mayor sea el valor absoluto de a, |a|, más
pasa por su vértice.
cerrada será la parábola.
Si a > 0 el vértice de es un mínimo absoluto. Es una función convexa Si a < 0 el vértice es un máximo absoluto. Es una
(tiene forma de U)
función cóncava (tiene forma de ∩)
Operaciones y propiedades de funciones: simetrías, funciones pares e impares.
C om pos ic ión de func ione s
Si te ne mo s d o s fu n ci on e s: f(x) y g(x), d e mod o qu e e l do mi ni o de l a 2 ª esté
in cl ui d o en el re co rri d o de l a 1 ª, se p ue d e de fi n i r un a nu e va fu n ci ón q u e a so cie
a cad a e l e me n to de l d o mi n io de f(x) e l va l o r d e g [f(x) ] .
(g o f) (x) = g [f( x)] = g (2 x) = 3
(2 x) +1 = 6 x + 1
(g o f) (1 ) = 6 · 1 + 1 = 7
Ej e mp lo s
1 S ea n l a s fu n cio n e s:
1 C al cu la (f o g ) (x)
2 C al cu la (g o f) (x)
2
1
2
3
1
Ca l cul a (f o g ) (x)
(g o f) (x)
2
Simetría respecto del eje de ordenadas
http://www.vitutor.com/fun/5/c_3.html
Una función f es simétrica respecto del eje de ordenadas si es una función par, es decir:
Ejemplo
Simetría respecto al origen
Una función f es simétrica respecto al origen si es una función impar, es decir:
f(−x) = −f(x)
Ejemplo
f(−x) = f(x)
Periodicidad. Acotación. Monotonía. Máximos y mínimos absolutos y relativos.
En la siguiente imagen puedes ver la gráfica de las temperaturas a lo largo de un día en una ciudad
española. En el eje OX están representadas las horas del día y en el eje OY las temperaturas en grados
centígrados.
Horas del día - Temperaturas (ºC)
(a) ¿Qué temperatura hizo a las 0 horas? ¿Y a las 10
horas? ¿Son esos puntos significativos?
(b) ¿Qué se podría afirmar acerca del
crecimiento y decrecimiento de la temperatura (monotonía)?
(c) ¿Se mantuvo constante la temperatura en algún intervalo del día? ¿Cuál fue el valor de la
temperatura en dicho intervalo?
(d) ¿A qué hora se alcanzaron las temperaturas máximas y mínimas? ¿Cuáles fueron los valores de
dichas temperaturas?
(e) ¿Son máximos/mínimos absolutos o relativos?
(f) ¿En qué tramo horario se alcanzaron temperaturas bajo cero?
Solución: (a) A las 0 horas, 2ºC. A las 10 horas, 0ºC. Claro que son significativos. Son los puntos de
corte con los ejes. El primero es el punto de corte con el OY y el segundo con el eje OX.
(b) La temperatura va descendiendo hasta las 4 de la madrugada donde se alcanzan -5 ºC (cinco grados bajo
cero). Se mantiene constante desde las 4 hasta la 6, donde empieza a subir hasta las 16 horas cuando se
alcanza una temperatura de 7ºC, comenzando a descender desde ese momento hasta las 24 horas cuando se
alcanza 1ºC.
Decrece en [0,4] y [16,24] - Constante en [4,6] - Crece en [6,16]
(c) Constante en [4,6]. Temperatura constante de -5ºC
(d) La máxima se alcanzó a las 16 horas con un valor de 7ºC. La mínima se alcanzó desde las 4 a las 6 de la
madrugada con un valor de -5ºC
(e) Tanto el máximo como los mínimos son absolutos. No hay ninguna hora del día en las que se alcancen
temperaturas por encima y por debajo, respectivamente, que en esas horas.
(f) Temperaturas bajo cero se alcanzaron desde un poco antes de la 1 de la madrugada hasta las 10 de la
mañana.
Periodicidad.
Una función es periódica cuando:
La función se repite de T en T, siendo T el período.
Ejemplos
1. La función f(x) = x − E(x), es periódica de periodo 1.
2. sen (x + 2π) = sen x
En el caso de la función seno T = 2π
3. tg (x + π) = tg x
En el caso de la función tangente T = π
Acotación.
http://www.vitutor.com/fun/2/a_8.html
Una función f está acotada
superiormente si existe un número
real k tal que para toda x es f(x) ≤
k.
El número k se llama cota superior.
k=0.135
Función acotada inferiormente
Una función f está acotada inferiormente si existe un número real k′ tal que para toda x es f(x) ≥ k
′.
El número k′ se llama cota inferior.
k′ = 2
Función acotada
Una función está acotada si lo está superior e inferiormente.
k′ ≤ f(x) ≤ k
k=½
Monotonía
k′ = -½
1. Monotonía (Crecimiento-decrecimiento)
Básicamente una función es creciente si, al aumentar
la variable independiente, x, también aumenta el valor
de la función, f(x). Es decreciente, si al aumentar el
valor de x, disminuye el de f(x). No olvides que las
gráficas se "leen" de izquierda a derecha.
Máximos y mínimos absolutos y relativos.
Extremos absolutos.
· Una función f alcanza su máximo absoluto en el punto x=a si es creciente a la izquierda de este punto
y decreciente a su derecha. El valor de la ordenada (coordenada y) en el máximo es mayor o igual que en
cualquier otro punto del dominio de la función.
· Una función f alcanza su mínimo absoluto en el punto x=b si es decreciente a la izquierda de este
punto y creciente a su derecha. El valor de la ordenada (coordenada y) en el mínimo es menor o igual que
en cualquier otro punto del dominio de la función.
Pero, en ocasiones, hay otros puntos que destacan entre los de su entorno más cercano, son los:
Extremos relativos.
· Una función f tiene un máximo relativo en el punto x=a si f(a) es mayor o igual que en todos los
puntos próximos al punto x=a, tanto por la derecha como por la izquierda de él.
· Una función f tiene un mínimo relativo en el punto x=b si f(b) es menor o igual que en todos los
puntos próximos al punto x=b, tanto por la derecha como por la izquierda de él.

Del mismo modo que hay puntos importantes como los extremos, existen otros que presentan una
singularidad especial. Son los puntos de cortes con los ejes.
Ejercicio n° 1
Considera la siguiente gráfica correspondiente a una
función:
a) ¿Cuál es su dominio de definición?
b) ¿Tiene máximo y mínimo? En caso afirmativo,
¿cuáles son?
c) ¿En qué intervalos crece y en cuáles decrece?
Solución:
a) Dominio de definición: [-5, +«)
b) Sí tiene mínimo, pero no tiene máximo.
Tiene dos mínimos en los puntos (-5, 0) y (0, 0).
c) Es creciente en los intervalos (-5, -3) y (0, +«).
Es decreciente en el intervalo (-3, 0).
Ejercicio n° 2
Dada la siguiente función mediante su representación
gráfica, responde a las preguntas:
a) ¿Cuál es su dominio de definición?
b) ¿Es continua? Si no lo es, indica dónde es
discontinua.
c) ¿Cuáles son sus máximos y mínimos relativos?
Solución:
a) El dominio de la función es el conjunto de todos los valores reales salvo x = -3.
b) No es continua en x = -3 y x = 1.
c) Tiene un máximo relativo en el punto (0, 4).
3
Tiene un mínimo relativo en el punto de abscisa - —, y su valor es - 2.
Ejercicio n° 3
Representa gráficamente una función, f, que cumpla las siguientes condiciones:
a) Dom (f) = [-5, 6]
b) Crece en los intervalos (-5, -3) y (0, 6); decrece en el intervalo (-3, 0).
c) Es continua en su dominio.
d) Corta al eje X en los puntos (-5, 0), (-1, 0) y (4, 0).
e) Tiene un mínimo en (0, -2) y máximos en (-3, 3) y (6, 3).
Solución:
Estudio y representación de funciones elementales.
http://matefacil01.blogspot.com.es/2011/05/funcion-lineal.html
FUNCIÓN AFÍN
Una función afín es una función cuyo dominio son todos los números reales, cuyo recorrido
también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
La función afín se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación
canónica, en donde m es la pendiente de la recta y b es la altura a la que la recta corta al eje Y.
Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que
0x no se pone en la ecuación).
Esta es la gráfica de la función lineal y = 3x + 2
Vemos que m = 3 y b = 2
(de la forma y = mx + b)
Este número m se llama pendiente de la recta y es
la relación entre la altura y la base, aquí vemos que
por cada unidad recorrida en x la recta sube 3
unidades en y por lo que la pendiente es m = 3.
b es la altura a la que la recta corta al eje Y (donde la
recta se cruza con el eje Y)
Volvamos al ejemplo de las funciones lineales
f(x) = 3x+2
Si x es 3, entonces f (3) = 3*3+2 = 11
Si x es 4, entonces f (4) = 3*4+2 = 14
Si x es 5, entonces f (5) = 3*5+2 = 17
Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa
en 3 unidades. Si el valor de la pendiente es positivo la función es Creciente.
Re pr e se nta c ión grá fic a de la pa r á bola
P od e mo s co n strui r un a p a ráb o la a pa rti r de esto s pu n to s:
1 . Vé r tic e
P o r el vé rti ce p a sa e l ej e d e si me tría d e l a pa rá b ol a .
2 . P untos de c or te c on e l e je OX
E n e l ej e de ab sci sa s la seg u n da co o rde n a da e s ce ro , p o r lo qu e te n d re mo s qu e
re so l ve r l a e cu a ció n ax ² + bx + c = 0
para resolverla usamos la fórmula:
Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de
intersección de la parábola con el eje de las X (abscisas).
Respecto a esta intersección, se pueden dar tres casos:
Que corte al eje X en dos puntos distintos s i b² − 4 a c > 0
Do s pu n to s d e co rte : (x 1 , 0 ) y (x 2 , 0 )
Que corte al eje X en un solo punto (es tangente al eje x) s i b² − 4 a c = 0
Un pu n to d e co rte : (x 1 , 0 )
Que no corte al eje X s i b ² − 4 a c < 0
Ningún punto de corte
3 . Pu n to de co rte co n e l e je OY
E n el ej e d e o rd e n ad a s la p ri me ra co o rd en a d a e s ce ro , p o r lo qu e te n d re mo s:
f ( 0 ) = a · 0 ² + b · 0 + c = c ( 0 , c ) Punto de corte en el eje de las ordenadas (eje Y)
(0, c)
Gráfica de las funciones cuadráticas
La función cuadrática más sencilla es f(x) = x2 cuya gráfica es:
x
-3 -2
-1 -0'5 0
0'5
1
2
3
f(x) =
9
4
1 0'25 0 0'25 1
4
9
x2
Esta curva simétrica se llama parábola.
Funciones cuadráticas más complejas se dibujan de la misma forma.
Dibujemos la gráfica de f(x) = x2 -2 x - 3.
x
-1 0
1
2
3
4
f(x) 0 -3 -4 -3
0
5
Completando la gráfica obtengo:
Funciones de proporcionalidad inversa.
http://www.hiru.com/matematicas/funcion-de-proporcionalidad-inversa
En el mundo real se producen con frecuencia situaciones en las que se relacionan dos variables de manera que su
producto siempre permanece constante. Así sucede, por ejemplo, cuando se pretende determinar el caudal de un
grifo necesario para llenar un depósito en un cierto tiempo: al aumentar el caudal, se reduce el tiempo, y a la
inversa. Estas relaciones se conocen genéricamente con el nombre de funciones de proporcionalidad inversa.
Relación de proporcionalidad inversa
Se denomina relación de proporcionalidad inversa a la que se establece entre una variable
independiente x y una variable dependiente y, de tal forma que el producto de ambas es siempre igual
a una constante k. Es decir: x  y = k.
Esta relación puede expresarse a modo de una función real de variable real, llamada función de
proporcionalidad inversa, que se escribiría genéricamente del modo siguiente:
Esta función estaría definida en todo el conjunto de los números reales excepto el punto para el cual se
anula el denominador (esto es, para x = 0).
Representación gráfica
Si se analiza la expresión de la función de proporcionalidad inversa, suponiendo que la constante k >
0, se advierte que:



La función no está definida para x = 0.
Para valores de x > 0, la función es positiva, de manera que tiende a infinito para valores muy pequeños de x
y se aproxima a cero conforme aumenta la variable independiente.
Análogamente, cuando x < 0, la función toma valores negativos de manera que tiende a menos infinito
cuando x tiende a cero y se aproxima a cero cuando x tiende a menos infinito.
De todo ello se deduce que la función de proporcionalidad inversa, para k > 0, se representa a modo
de una gráfica de dos ramas simétricas con respecto al origen y con respecto a la bisectriz del
segundo y el cuarto cuadrantes del plano.
Representación gráfica de la función de proporcionalidad inversa para k > 0.
Funciones definidas a trozos.
Son funciones que están definidas por expresiones algebraicas distintas para determinados
intervalos reales.
Ejercicio 1: Representa la función definida a trozos:
Ejercicio 2: Representa la función definida a trozos:
Solución:
Ejercicio 3: Representa la función definida a trozos:
Solución:
Ejercicio 4: Representa la función definida a trozos: f(x) = E (x)
x
0 0.5 0.9 1 1.5 1.9 2
f(x) = E(x) 0
0
0
1
1
1
1
Ejercicio 5: Representa la función definida a trozos:
x
0
0.5
0.9
1
1.5
1.9
2
f(x) = x − E(x) 0
0.5
0.9
0
0.5
0.9
0
f(x) = x − E (x)
Func ión va lor a bs oluto
La s fu n cio n e s en va l o r a b so l u to se tra n sfo rma n e n fu n ci o n e s a tro zo s, sig u i en d o
lo s si g ui e n te s p a so s:
1 . S e i gu a l a a ce ro la fun ci ó n , si n el va l o r a b so l u to , y se cal cu l an su s ra íce s.
2 . S e fo rma n i n te rva l o s co n la s ra íce s y se e va l ú a e l sig n o d e ca da in te rva l o .
3 . De fi ni mo s l a fu n ci ón a tro zo s, te ni e nd o e n cu e n ta qu e en lo s i n te rva l o s do n de
la x e s ne g a ti va se ca mbi a e l si gn o d e l a fu n ci ó n .
4 . R ep re se n ta mo s la fu n ci ón re su l ta n te .
Ej e mp lo s
1.
D =
2.
D =
Ejemplos del valor absoluto de una función
1) f(x) = | 3x - 2 |
Dom(f) = R
Im(f) = [0, +∞)
Puntos de corte:
Para x = 0 sustituimos en:
f(0) = - 3·0 + 2 = 2
El punto de corte es: (0, 2)
Para que f(x) = 0 se tiene que:
3x - 2 = 0 → x = 2/3
El punto de corte es: (2/3, 0)
2) f(x) = | x2 - 5x + 5 |
Resolvemos la inecuación: x2 - 5x + 5 ≥ 0
x2 - 5x + 5 = 0
• Intervalo A: x = 0
⇒
x2 - 5x + 5 = 5 > 0
• Intervalo B: x = 3
⇒
x2 - 5x + 5 = 32 - 5·3 + 5 = - 1 < 0
• Intervalo C: x = 4
⇒
x2 - 5x + 5 = 42 - 5·4 + 5 = 1 > 0
Por tanto, tendremos que x2 - 5x + 5 ≥ 0 en los intervalos A y C .
Y será x2 - 5x + 5 < 0 únicamente en el intervalo B .
La función queda:
Dom(f) = R
Im(f) = [0, +∞)
Puntos de corte:
Para x = 0 sustituimos en:
f(0) = 02 - 5·0 + 5 = 5
El punto de corte es: (0, 5)
Para que f(x) = 0 se tiene que:
x2 - 5x + 5 = 0 , es decir:
Llamamos función exponencial a la que tiene por expresión analítica y=ax, siendo a un número real
positivo distinto de 1.
Son funciones continuas cuyo dominio es el conjunto de los números reales. Son funciones positivas que
pasan por los puntos (0,1) y (1,a).
Si a>1, son funciones crecientes en todo su
dominio.
Para valores de x muy grandes pero negativos, f(x)
toma valores próximos a cero.
Para valores de x muy grandes, f(x) toma valores
también muy grandes.
Cuanto mayor sea el valor de a, más rápido crecen
estas funciones.
Si 0<a<1, son funciones decrecientes en todo su dominio.
Para valores de x muy grandes pero negativos, f(x) toma valores muy grandes.
Para valores de x muy grandes, f(x) toma valores próximos a cero.
Cuanto menor sea el valor de a, más rápido decrecen estas funciones.
Función logaritmo
Al ser f y g funciones inversas, sus gráficas son simétricas respecto de la bisectriz del primer
cuadrante. Para dibujar y=logx intercambiamos los valores de la x y de la y respecto de la gráfica de
y=10x.
Función seno
f(x) = sen x
Dominio:
Recorrido: [−1, 1]
Período:
Continuidad: Continua en
Impar: sen(−x) = −sen x
Función coseno
f(x) = cos x
Dominio:
Recorrido: [−1, 1]
Período:
Continuidad: Continua en
Par: cos(−x) = cos x
Función tangente
f(x) = tg x
Dominio:
Recorrido:
Continuidad: Continua en
Período:
Impar: tg(−x) = −tg x
Sucesiones: idea intuitiva de límite.
http://www.ehu.es/juancarlos.gorostizaga/apoyo/sucesiones.htm
Se llama sucesión de números reales, a una lista infinita de números reales:
A cada uno de estos números se le llama término (primer término, segundo, etc.). De una manera
matemática una sucesión se suele definir como una aplicación de N* en R, dada por:
es decir, para n=1 tenemos el primer término, para n=2 el segundo, ...
A las sucesiones se las suele representar por su término general, que es un término genérico dependiente de
n, tal que al ir dando a n los sucesivas valores de N* vamos obteniendo todos los términos de ella. Por
ejemplo, la sucesión:
es la formada por:
En concreto, en esta sucesión hay dos aspectos destacables, observémosla más detenidamente dibujándola
sobre la recta real:
Por una parte, podemos notar que todos sus infinitos términos se encuentran comprendidos entre 0 y 1.
Cuando esto sucede se dice que la sucesión está acotada (superiormente por el 1, e inferiormente por el 0).
En caso de que esto no fuera así, se hablaría de una sucesión no-acotada (bien superiormente, bien
inferiormente, o incluso puede ser no-acotada en ambos lados).
El segundo aspecto destacable es que cada término es inferior al que le antecede (los términos se
encuentran colocados sobre la recta real de derecha a izquierda) lo cual indica que la sucesión es
decreciente. En caso opuesto como sucede con la sucesión (2, 4, 6, 8, 10, ...) se dice que la sucesión es
creciente.
Idea intuitiva de límite
En la sucesión an = 1/n, observamos que los términos se van acercando a cero.
Consideremos que 0 es el límite de la sucesión porque:
1. Los términos se aproximan a cero tanto como se quiera a medida que se avanza en la sucesión.
2.La distancia a cero puede ser tan pequeña como queramos.
d(1, 0) = 1
d(1/10, 0) = 0.1
d(1/100, 0) = 0.01
d(1/1000, 0) = 0.001
...
d(1/1 000 000, 0) = 0.000 001
...
d(1/1 000 000 000) = 0.000 000 001
Vemos que el límite es 0, pero no hay ningún valor de la sucesión que coincida con el límite.
Cálculo de límites sencillos de sucesiones: indeterminaciones.
Calcular los límites:
Soluciones:
1
2
3
4
5
Hallar los límites:
Soluciones:
1
2
Calcula los siguientes límites:
Soluciones:
1
2
3
4
5
Hallar los límites:
Soluciones:
1
2
Se transforma a
3
4
Idea intuitiva de límite de funciones.
Calcula los siguientes límites a partir de
esta gráfica. En caso de no existir escribe
no
f(8)=
f(4)=
Calcula los siguientes límites a partir de la gráfica que te proponemos:
Las soluciones deben coincidirte con estas:
1: -1
6: +∞
2: 1
7: +∞
3: 1
8: -∞
4: No existe (límites laterales distintos)
5: +∞
9: -2
10: 1
www.madrid.dominicasanunciata.com/...Madrid/.../ LÍMITES.doc
Una función polinómica es una función del tipo:
Para estudiar el cálculo de su límite, se distinguirán dos casos:
El límite de una función polinómica en un punto x0 es igual al valor que toma la función en ese punto:
B. Límite de una función polinómica en el infinito
El límite de una función polinómica en el infinito es +∞ o -∞, dependiendo de que el coeficiente del término de mayor
grado del polinomio sea positivo o negativo:
Ejercicio:
Resolución:
Resolución:
8/3, es positivo.
Cálculo de límites de funciones racionales
Para estudiar el límite de una función racional, se distinguirán dos casos:
Puesto que una función racional es el cociente de dos polinomios, para calcular su límite puede aplicarse la regla para el
cálculo del límite de un cociente de dos funciones:
Tanto el límite del numerador como el del denominador son límites de funciones polinómicas, cuyo cálculo se explicó en el
apartado anterior.
Al efectuar estos límites pueden darse varias situaciones.
Se calculan en este caso los límites de P(x) y Q(x) como funciones polinómicas y se halla su cociente.
Si el denominador se anula en x0, puede ocurrir que el numerador también se anule en x0, o que el numerador no se anule
en x0.
Para resolver esto basta con tener en cuenta que si Q(x0) = 0 y P(x0) = 0, x0 es raíz
Una vez hecha la simplificación, bien dividiendo P(x) y Q(x) entre x - x0 ó bien aplicando la regla de Ruffini, se vuelven a
calcular los límites de los polinomios ya simplificados.
A.2.2. El límite del numerador no es cero.
Para resolver esta indeterminación es necesario estudiar los límites laterales de la
Si ambos límites laterales son iguales, la función tiene por límite su valor. Si no son iguales, la función no tiene límite.
Ejercicio:
Resolución:
Resolución:
Esta indeterminación se resuelve simplificando el cociente. Aplicando la regla de Ruffini, se obtiene la descomposición de
los polinomios P(x) = x3 - 2x2 - 6x +12 y
Q(x) = x2 + 3x -10.
 Descomposición factorial de P(x):
 Descomposición factorial de Q(x):
 El límite del cociente P(x)/Q(x) es:
Resolución:
 Se simplifican numerador y denominador:
Resolución:
 Para resolver la indeterminación se estudian los límites laterales de la función en el punto x0 = 3.
Resolución:
 Se estudian los límites laterales:
Como los dos límites laterales no coinciden, la función f(x) = 1/(x - 1) no tiene límite cuando x tiende a 1.
Límites infinitos y en el infinito: asíntotas verticales, horizontales y oblicuas.
Límite de una función racional en el infinito
Las reglas de cálculo de límites de funciones cuando x tiende a infinito son las mismas que las empleadas para límites de
sucesiones.
El límite de una función racional cuando x tiende a infinito es igual al límite del cociente de los términos de mayor grado
del numerador y denominador.
Si
El valor de este límite depende del valor que tengan n y m:

Si el grado del numerador es mayor que el grado del denominador (n > m), el límite es infinito, positivo o
negativo, dependiendo de que los signos de los cocientes an y bm sean iguales o distintos


Ejercicio:
Si el grado del numerador es igual que el grado del denominador (n = m),
Si el grado del numerador es menor que el grado del denominador (n<m), el límite es 0.
Resolución:
En este caso, el grado del numerador, 2, es mayor que el grado del denominador, 1, por tanto el límite es .
Resolución: El grado del numerador es mayor que el grado del denominador, y los términos de mayor grado tienen
signos distintos, por tanto:
Resolución: El grado del numerador es igual que el grado del denominador, por tanto:
Resolución: El grado del numerador es menor que el grado del denominador, por tanto:
Calcula los siguientes límites:
lim( x  x  x  1)  (  Ind .)  lim
2
a)
2
( x 2  x  x 2  1)( x 2  x  x 2  1)
x  x  x 1
2
x  
2

x  
 lim
( x 2  x ) 2  ( x 2  1) 2
x  x  x 1
2
2
 lim
x2  x  x2 1
 lim x  lim x  lim 1  1
xx
2x
2 2
x  x
x  
x  
lim( 4 x  2  2 x )  lim
x  
( 4 x 2  2  2 x)( 4 x 2  2  2 x)
4x 2  2  2x
x  
x  
x  
x  
 lim
x  
=
x2  x  x2 1
2
2
lim
x 1
  lim
x
2
x  
b)
x2  x  x2 1
x2  x  x2 1
 lim
x  
x  
lim
x 2  x  ( x 2  1)
4x 2  2  4x 2
4x 2  2  2x
 lim
x  
( 4 x 2  2 ) 2  (2 x) 2
4x 2  2  2x

x  
2
4x  2  2x
2
 lim
x  
2
4x  2x
2
 lim
2
2
1 1
 lim
 lim

0
2x  2x
4x
2x  
x  
x  
x  

Asíntotas verticales, horizontales y oblicuas.
Dada una función y=f(x) cuya gráfica es la curva C se dice que la recta r es una asíntota de
f(x) si la curva C se acerca a r indefinidamente sin llegar a coincidir con la propia r.
Como una asíntota es una recta, tenemos hasta tres posiciones distintas de una recta con
relación a los ejes.
Por ello, para cada función pueden existir hasta tres tipos distintos de asíntota.
La vertical existirá si el límite de la función tiende a infinito cuando x tiende a un
valor finito a, su valor será x=a.
La horizontal y la oblicua las encontraremos cuando estudiemos lo que ocurre
cuando la variable independiente tienda a más o menos infinito.
En el caso de funciones racionales podemos hacer un estudio particular para
saber qué tipos de asíntotas tendrán según sean el numerador y el denominador.
Sea a un número real, la recta vertical x=a es una asíntota vertical de la
función y=f(x) si se verifica alguna de las siguientes propiedades:
¿Cómo saber dónde buscar la asíntota vertical?



Si es una función polinómica, no tiene asíntotas de ningún tipo.
Si es una función racional, como vimos en el apartado anterior, tendremos que buscar
en las raíces del denominador.
Otra función que tiene asíntota vertical es la función logarítmica, más concretamente,
en los puntos extremos de los intervalos donde empieza el dominio.
y=ln(x)
El logaritmo tiene una asíntota vertical x=0
Tenemos la función
y queremos calcular sus asíntotas verticales,
Tendremos que estudiar para que valores el denominador x 2-1 es 0.
En este caso las posibles asíntotas verticales son x=1 y x=-1.
Para x=1
Tenemos que calcular el límite cuando x=1- y el límite cuando x=1+.

ya que cuando tomamos valores muy próximos a 1 por la izquierda,
el numerador tiende a 1 y el denominador a 0, pero por la izquierda, es decir, valores
negativos. Por lo tanto, el límite es menos infinito. La asíntota vertical es como la primera
imagen de la definición. Cuando nos acercamos a x=1 por la izquierda la gráfica de f(x)
tiende a -∞.

ya que cuando tomamos valores muy próximos a 1 por la derecha,
el numerador tiende a 1 y el denominador a 0, pero por la derecha, es decir, valores
positivos. Por lo tanto, el límite es más infinito. La asíntota vertical es como la última
imagen de la definición. Cuando nos acercamos a x=1 por la derecha la gráfica de f(x)
tiende a +∞.
x=-1
Tenemos que calcular el límite cuando x=-1- y el límite cuando x=-1+.

. Estamos en el caso 2 de la definición. Cuando nos acercamos a
x=-1 por la izquierda la gráfica de f(x) tiende a -∞.

, esto es, es similar a la tercera gráfica de la definición. Cuando
nos acercamos a x=-1 por la derecha, la gráfica de f(x) tiende a +∞.
Calcula, si las tienen, las asíntotas verticales de las siguientes funciones:
(a) Como tenemos una función racional, tienes
que estudiar los puntos en los que se anula el
denominador:
x - 2 = 0.
Calculamos
asíntota vertical en x=2.
.
Por
lo
tanto,
tiene
una
(b) Ahora tenemos otra función racional, tienes
que estudiar los puntos en los que se anula el
denominador: x2+1=0.
Como no se anula para ningún valor de x, no
tiene asíntotas verticales.
(c) Si tienes un logaritmo tienes que ver cuando,
en este caso, 1-x tiende a 0+.
El dominio de definición de la función son los
valores de x para los que 1-x>0 ⇒ 1>x ⇒ Dom
h=(-∞ , 1).
La asíntota vertical la encontraremos en x=1, pues cuando x →1-⇒ (1-x)→0+ y
.
Sea b un número real, la recta horizontal y=b es una asíntota horizontal de la
función y=f(x) si se verifica alguno de los siguientes límites:
En una empresa montan ordenadores en
cadena. Han contratado a un nuevo empleado
para la sección de discos duros. En esta sección
el número de montajes realizados por un
trabajador sin experiencia depende de los días
de entrenamiento según la función:
Imagen de jepoirrier bajo licencia Creative
Commons
, donde t viene expresado en días
(a)¿Cuántos montajes hará el primer día?¿y el noveno?¿y
al cabo de 30 días?¿Y a los dos meses?
El primer día realizará N(1)=8, es decir, 8 montajes.
N(9)=24, esto quiere decir que el noveno día ya montará 24 discos duros.
N(30)=29,09, es decir, montará aproximadamente 29 discos duros.
N(60)=30,48. Esto quiere decir que al cabo de
60 días montará casi 31 discos diarios.
(b)Si el empleado tiene un contrato indefinido,
¿cuántos ordenadores será capaz de montar por
término medio cuando lleve varios años en la
empresa?.
Aquí tenemos que estudiar lo que ocurre
cuando t se hace grande:
En este caso concreto:
Procediendo igual que en el tema anterior, nos quedamos con los términos de
mayor grado del numerador y denominador y simplificamos:
Por lo tanto, de media montará 32 discos duros diarios.
La recta y=32 es una asíntota de la función N(t).
Calcula, si las tienen, las asíntotas horizontales de las siguientes funciones:
(a) Como tenemos una función
racional y el grado del numerador
es
mayor
que
el
del
denominador,
no
tenemos
asíntotas horizontales.
(b) Ahora el grado del
numerador es igual al
grado del denominador.
En este caso existe una
asíntota horizontal.
Para hallar su ecuación
tenemos que calcular el
límite cuando x tiende a
más infinito y a menos
infinito.
. Esto quiere decir que
la asíntota horizontal es
y=1.
(c) Como el grado del numerador es menor que el
grado del denominador, tiene una asíntota
horizontal, pues
horizontal es y=0.
. Esto quiere decir que la asíntota
La recta horizontal y=mx+n, m≠0 es una asíntota oblicua de y=f(x) si se
verifica alguno de estos límites:
Para calcular la ecuación de la asíntota, y=mx+n, tendremos que calcular:
Calcula la asíntota oblicua de las siguientes funciones:
(a) Como la función es racional y el grado del numerador
es una unidad mayor que el del denominador, nuestra
función tiene una asíntota oblicua. Como sabemos que la
función es racional tiene la misma asíntota oblicua por los
dos lados. Vamos a calcularla en +∞.
Por lo tanto, la asíntota oblicua que buscamos es y=x+9
(b) Igual que en el apartado a, tenemos una
función racional donde el grado del numerador es
una unidad mayor que el del denominador, por lo
que nuestra función tiene una asíntota oblicua.
Vuelve a tener la misma asíntota oblicua por los
dos lados al ser una función racional. Vamos a
calcularla en +∞.
Por lo tanto, la asíntota oblicua que buscamos es y=2x+6
Ejercicio: Señala las asíntotas de cada una de las siguientes funciones. Para ello
escribe una ecuación de la forma x=2 si es vertical, y=-3 si es horizontal e
y=2x+1 si es oblicua. En caso de que no tenga alguna de ellas escríbelo.
apartado (a)
apartado (b)
apartado (c)
apartado (d)
Determina los límites en el infinito de las siguientes funciones y escribe la ecuación de sus asíntotas horizontales.
.
lim f ( x )  0; lim f ( x )  
No lim f ( x)  0; lim f ( x )  1
lim f ( x )  1 lim f ( x)  1
x  
x  
x  
x  
A. H. en y=0 (por izda.)
x  
A. H. en y=-1 (por dcha.)
x  
A.H. en y=-1 (por izda.)
A. H. en y=1 (por dcha.)
Calcula la ecuación de las asíntotas horizontales, si las tiene, de las siguientes funciones:
a) f(x)=
3x  1
1  2x 2
x2 1
4x 2  1
b)
f(x)=
c)
f(x)=
d)
f(x)=
2x  1
x2 1
x3
2x  2
Solución:
1  2x 2
 2x 2
1  2x 2
 2x 2
 lim 2  2; lim 2
 lim 2  2  y  2. A.H .
1  2 x 2 lim 2
a) f(x)= 2
;
x 1
x
x 1
x
x  1 x 
x  
3x  1
3x 3
3x  1
3x 3
 lim
 ; lim
 lim

3 x  1 lim
3
b) f(x)=
;
2x  1
2x 2
2x  1
2 x 2  y  . A.H .
2 x  1 x 
2
x  
x2 1
x2
1
1
 0;
x 2  1 lim 3  lim 3  lim 
 y  0. A.H .
c) f(x)=
;
x 
x
x
3
x
x  
d) f(x)=
4x 2  1 ;
4x 2  1
4x 2  1
4x 2
2x
lim
 lim
 lim
 lim
 1  y  1 A. H. (por izda.)
2x  2
2x  2
 2x  2
 2x
 2x
x  
x  
x  
x  
lim
4x 2  1
4x 2
2x
 lim
 lim
 1  y  1 A. H. (por dcha.)
2x  2
2x
2x
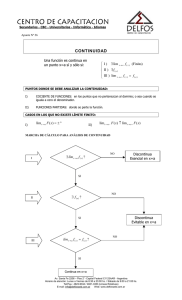
Concepto de continuidad de una función: discontinuidades.
Las tres posibilidades de discontinuidad.
Discontinuidad evitable
Discontinuidad de salto
infinito
Discontinuidad de salto finito
Vamos a comenzar con la primera. ¿Por qué se produce una discontinuidad
evitable?
Si te fijas en la primera gráfica, si nos acercamos en el eje X a 1, la función,
tanto por la izquierda como por la derecha de 1, se acerca a -7. El problema está
en que justo cuando llegamos al valor x=1, la función se va al 2 en lugar de -7.
Por tanto, lo que ocurre aquí es que límite e imagen de la función no coinciden:
Si te fijas, en todos los otros puntos esto sí se cumple, el límite de la función
coincide con el valor de la imagen.
La segunda discontinuidad que aparece es la de salto infinito. ¿Por qué en x=3
hay una discontinuidad de salto infinito? La respuesta es clara, porque cuando
nos acercamos a x=3, la función se va hacia infinito; a -∞ por la izquierda y a
+∞ por la derecha, o sea, cuando al hacer el límite en el punto el resultado es
infinito:
Si recuerdas, esto ocurría en las indeterminaciones k/0.
Por último, la tercera gráfica no es continua porque en x=1 hay un salto. ¿Qué
es lo que ocurre para que haya esa discontinuidad de salto finito? Pues que
cuando nos acercamos a 1, la función se acerca a distintas cosas según por el
lado que lo hagamos, por la izquierda se acerca a -7 y por la derecha a 3. Luego,
lo que ocurre, es que los dos límites laterales existen, son números reales, pero
no coinciden.
Si te fijas en todos los otros puntos esto sí se cumple, los límites laterales
coinciden.
Teniendo en cuenta lo que acabamos de ver, una función es continua en x = a
si:
1.
2.
3.
Existe f(a).
Los dos límites laterales existen, son números reales y coinciden.
El valor del límite coincide con el de la imagen.
Esas tres propiedades se resumen en:
Ejercicio 1: Estudia la continuidad de la función
Solución: Tanto para valores menores que dos, como para valores mayores que 2, la función está
definida como una semirrecta, es decir un trozo de una línea recta (función afín). Luego para estos
puntos la función es continua. El único punto problemático es x = 2, donde tenemos que ver si los
límites laterales a izquierda y derecha deben coincidir con la imagen de la función en 2.
Luego, la función es continua en toda
Ejercicio 2: Estudia la continuidad de la función
Solución: Tanto para valores menores que 0, como para valores mayores, la función está definida
como un trozo de una línea recta (función afín). Luego para estos puntos la función es continua. El
único punto problemático es x = 0, donde tenemos que ver si los límites laterales a izquierda y
derecha deben coincidir con la imagen de la función en 0.
|−1 − (−3)| = 2
La función es discontinua inevitable de salto 2 en x = 0.
Ejercicio 3: Estudia la continuidad de la función
Solución: La función es continua en todo R menos en los valores que se anula el
denominador, si igualamos éste a cero y resolvemos la ecuación obtendremos los puntos de
discontinuidad.
x = −3; y resolviendo la ecuación de 2º grado obtenemos también: x=2−√3 y x=2+√3
La función tiene tres puntos de discontinuidad en x=−3, x=2−√3 y x=2+√3
Ejercicio 4: Estudia, en el intervalo (0,3), la continuidad de la función:
Solución: Sólo hay duda de la continuidad de la función en los puntos x = 1 y x = 2, en los que
cambia la forma de la función.
En x = 1 tiene una discontinuidad de salto 1.
En x = 2 tiene una discontinuidad de salto 1.
Ejercicio 5: Dada la función:
1 Demuestra que f(x) no es continua en x = 5.
2 ¿Existe una función continua que coincida con f(x) para todos los valores x ≠ 5? En caso
afirmativo, da su expresión.
Solución: Para demostrar que f(x) no es continua en x = 5, calculamos
f(5) = 0.
Resolvemos la indeterminación:
f(x) no es continua en x = 5 porque:
2 ¿Existe una función continua que coincida con f(x) para todos los valores x ≠ 5? En caso
afirmativo dar su expresión.
Si
la función sería continua, luego la función redefinida es:
dicha función ya es continua en 5 y por tanto en
,
todo R. Dicha función es precisamente f(x) = x + 5
Ejercicio 6: Estudia la continuidad de la función:
Solución: La función f(x) es continua para x ≠ 0. Vamos a estudiar la continuidad en x = 0.
La función no es continua en x = 0, porque no está definida en ese punto.
Ejercicio 7: Estudia la continuidad de la función f(x) = x · signo(x).
Solución:
La función signo de x está definida por
La función es continua en toda
.
Ejercicio 8: Calcula el valor de a para que la función siguiente sea continua:
Solución: Para que sea continua en x=1, deben coincidir los límites laterales.
x3-2x+k,
si x  3
7
si x=3
Ejercicio 9: Calcula k para que la función y=f(x) sea continua en  : f(x)=
Solución:
lím f(x) = 33 – 2.3+k=3+k
x 3
f ( x)  f (3)  3+k=7  k = 4
Para que sea continua en x=3  lím
x 3
f(3)=7
Ejercicio 10: Cada una de las siguientes funciones tiene uno o más puntos donde no es continua. Indica cuáles son
estos puntos y qué tipo de discontinuidad presenta:
a) y =
x2
x3
b) y =
x 2  3x
x
c) y =
x2  3
x
3 si x  4
d) y=
2 si x=4
Solución:
a) y =
x2
x3
lím f(x)= lím x  2  3  2 
x3
x 3
x  3 3  3
lím f(x)= lím x  2  3  2 
x3
x 3
x  3 3  3
b) y=
x 2  3x
x
5
 
0
5
 
0
f discontinua inevitable de salto infinito en x=3
f continua en   {3}
2
lím f(x) = lím x  3 x   0 In det   lím x( x  3)  lím ( x  3)  3
x0
x 0
x 0
x
x
0
 x 0
No existe f(0), ya que f(0)=
c) y=
0
 f discontinua evitable en x = 0  f continua en   {0}
0
x2  3
x
2
lím f(x) = lím x  3   3  
x 0
x 0
x
0
f discontinua de salto infinito en x=0
2
lím f(x) = lím x  3   3  
x0
x0
x
0
f continua en   {0}
3 si x  4
d) y=
1 si x=4
lím
lím 3  3
x  4 f(x) = x4
f discontinua evitable en x=4
F(4)=1
f continua en   {4}
Ejercicio 11: Calcula el valor de los siguientes límites:
a) lím
x 0
3
x2
b) lím
x4
x 2  3x  5
Solución:
a) lím
x 0
3
3
3

=
x2 2
2
b) lím
x4
x 2  3x  5 = 2 2  3.2  5  4  6  5  3
Ejercicio 12: Calcula los límites de las funciones siguientes en los puntos que se indican. Donde convenga especifica el
valor del límite a la izquierda y a la derecha del punto. Representa gráficamente los resultados:
a) f(x)=
x3
, en – 2 , 0 y 2
x2  4
Solución:
a) f(x)=
b) f(x)=
4 x  12
en 2, 0 y 3
( x  2) 2
x 3 , en –2, 0 y 2
x2  4
3
8
8
lím f(x) = lím x
 
   
x( 2 )
x ( 2 )
2
x 4 4 4 0
3
8
8
lím f(x) = lím x
 
   
x( 2 )
x ( 2 )
2
x 4 4 4 0
c) f(x) =
x 2  2x  1
en 0 y –3
x 2  2x  3
x3
0

0
2
x 4 04
x3
0
lím f(x) = lím

0
x0
x 0
2
x 4 04
lím f(x) = lím
x 0
x 0
lím f(x) =0
x 0
f(0)=0
f continua en x=0
x3
8
8
 
   
2
x 4 4 4 0
3
8
8
lím f(x) = lím x
 
   
x2
x 2
2
x 4 4 4 0
lím f(x) = lím
x2
x 2
b) f(x)=
4 x  12
en 2, 0 y 3
( x  2) 2
lím f(x) = lím 4 x  12  8  12   4   4  
x 2
x 2
( x  2) 2 (2   2) 2 (0  ) 2 0 
lím f(x) = lím 4 x  12  8  12   4   4  
x 2
x 2
( x  2) 2 (2   2) 2 (0  ) 2 0 
lím f(x) = lím 4 x  12   12  3
x 0
x 0
( x  2) 2 (0  2) 2
lím f(x) = – 3 = f(0)  f continua en x=0
x 0
lím f(x) = lím 4 x  12   12  3
x 0
x 0
( x  2) 2 (0  2) 2
lím f(x) = lím 4 x  12  12  12  0  0  0
x3
x 3
( x  2) 2 (3   2) 2 (1 ) 2 1
lím f(x) = lím 4 x  12  12  12  0  0  0
x3
x 3
( x  2) 2 (3   2) 2 (1 ) 2 1
c) f(x) =
lím
 f continua en x=3
x 3 f(x) = f(3) = 0
x 2  2x  1
en 0 y –3
x 2  2x  3
2
lím
lím x  2 x  1  1   1  f (0)  f continua en x=0
x 0 f(x) = x0
3
x 2  2x  3  3
2
lím f(x) = lím x  2 x  1  9  6  1  16  
x( 3 )
x ( 3 )
x 2  2x  3 9  6  3 0
f discontinua de salto en x = – 3
2
lím f(x) = lím x  2 x  1  9  6  1  16  
x( 3 )
x ( 3 )
x 2  2x  3 9  6  3 0
Ejercicio 13: Calcula el valor del límite cuando x   de las siguientes funciones:
a) f(x)= –x2+3x+5
b) f(x)=5x3+7x
c) f(x)=x–3x4
d) f(x)=
1
3x
e) f(x)= –
1
x2
f) f(x)=
x3  1
5
Solución:
a) f(x)= –x2+3x+5;
lím f(x) = – 
b) f(x)=5x3+7x;
x (  )
lím f(x) = – 
x(  )
1
1
0
; xlím
(  ) f(x) =
3x

1
1

x 3  1 lím

0
 
e) f(x)= – 2 ; xlím
f(x)
=
f)
f(x)=
; x(  ) f(x) =
(  )

5
x
5
x 2  3 x  11
Ejercicio 14: Halla las asíntotas verticales y sitúa la curva respecto de ellas: a) y=
x 1

c) f(x)=x–3x4; xlím
(  ) f(x) = –
d) f(x)=
b) y=
x 2  3x
x 1
Solución:
a) y=
x 2  3 x  11
x 1
x+1=0;
x=–1 asíntota vertical.
Para situar la curva hallamos los límites laterales.
2
lím x  3 x  11 = 1  3  11  15  
x ( 1 )
 1  1 0 
x 1
2
lím x  3 x  11 = 1  3  11  15  
x ( 1 )
 1  1 0 
x 1
b) y=
x 2  3x
x 1
x+1=0;
x=–1 asíntota vertical.
Para situar la curva hallamos los límites laterales.
2
lím x  3 x = 1  3  4  
x ( 1 )


x 1 1 1 0
2
lím x  3 x = 1  3  4  
x ( 1 )


x 1 1 1 0
Ejercicio 15: Halla las asíntotas verticales y sitúa la curva respecto de ellas: a) y=
x2  2
x 2  2x
b) y=
x2  2
x 2  2x  1
Solución:
a) y=
x2  2
x 2  2x
x2 – 2x=0;
x(x– 2)=0;
x=0 o x=2 asíntotas verticales.
Para situar la curva hallamos los límites laterales.
2
2
2
x 2  2 lím x  2
   
=
=


x 0
x
0
x( x  2) 0 (2) 0
x 2  2x
2
2
2
2
lím x  2 = lím x  2 =
   


x2
x 2
2
x( x  2) 2 (2  2) 0
x  2x
lím
2
2
lím x  2 = lím x  2 = 2  2  


x0
x 0
x( x  2) 0 (2) 0
x 2  2x
2
2
6
6
lím x  2 = lím x  2 =
   


x2
x 2
2
x( x  2) 2 ( 2  2) 0
x  2x
b) y=
x2  2
x 2  2x  1
x2–2x+1=0;
x=
1 11
 1;
1
x=1 asíntota vertical.
Para situar la curva hallamos los límites laterales.
lím
3
3
3
x2  2
x2  2
lím


 
=
=


2

2
x1
(0 )
0
( x  1) 2 (1  1)
x 2  2x  1
lím
3
3
3
x2  2
x2  2
lím


 
=
=


2

2
x1
(0 )
0
( x  1) 2 (1  1)
x 2  2x  1
x 1
x 1
Ejercicio 16: Halla las asíntotas y sitúa la curva respecto de ellas:
a) y=
x
1 x2
b) y=
x3
;
1 x2
Solución:
a) y=
x
1 x2
lím f(x)=lim
x (  )
x
x / x2
1/ x
0
lím
=
 xlím

 0; y=0 asíntota horizontal.
x

(

)
2
2
2
2
2
 (  )
1 x
1/ x  x / x
1/ x  1 0  1
Para hallar la posición hallo el signo del límite de la curva menos la asíntota:
x
1
1
 x

lím (f(x)-0)= xlím
 0  = xlím
 xlím

 0 
(  )
(  ) 
2
2
(  )
x
x 
1 x

x(  )
x  
x  
x  
x  
 C  A  0  C  A  La curva va por encima de la asíntota en el +  , haríamos lo mismo en el – 
x3
b) y=
; gr(numerador)=grado (denominador)+1
x3
|_x2+1______
2
1 x
– x3– x
------–x
y=
x
x
x3
 y=x Asíntota oblicua.
=x2
1 x2
1 x
Para estudiar la posición de la curva respecto de la asíntota estudio el signo del límite de la curva C menos la asíntota A
x3
x
– x=
2
1 x
1 x2
 x3

x
x lím 1
1
lím
lím

 x  = xlím
 0 ;
(C–
A)=
= xlím
= x(  ) 
x(  )
x(  ) 
(  )
(  )
2
2
2
1

x
x
x


1 x


 C  A  0  C  A  La curva va por encima de la asíntota, en el +  , haríamos lo mismo en el –  .
C– A=
Ejercicio 17: Representa las siguientes funciones y explica si son discontinuas en alguno de sus puntos.
2x–1 si x<3
1
si x  0
x2 – 2 si x<2
a) f(x)=
b) f(x)=
c) f(x)=
2
5–x si x  3
x +1 si x>0
x
si x>2
Solución:
lím f(x) = lím (2x–1)=2.3–1=5; lím f(x) = lím (5–x) =5–3 =2  f discontinua de salto en x=3
x3
x 3
x 3
x 3
Ya que lim f(x)=5  lim f(x) =2=f(3)  f(x) continua en  – {3}
x 3
x 3
si x  0
1
b) f(x)=
x 2+1 si x>0
lím f(x) = lím (1) = 1 = f(0); lím f(x) = lím (x2+1) = 1  f continua en x = 0
x0
x0
x 0
x 0
Ya que lím
f(x) = 1 = f(0) = lím
f(x)
x0
x 0 
c) f(x)=
x2 – 2
si x<2
x
si x>2
 f continua en todo 
lím f(x) = lím (x2–2) = 4 – 2 = 2 = lím f(x) = lím x = 2   lím f(x)=2 pero no existe f(2) 
x2
x2
x 2
x 2
x2
f(x) discontinua evitable en x = 2 
f(x) continua en  – {2}
Ejercicio 18: a) Halla el límite de las funciones del ejercicio anterior para x=–3 y para x=5.
b) Halla, en cada una de ellas, el límite cuando x    y cuando x    , 
Solución:
f(x)=
f(x)=
2x–1 si x<3
lím f(x) = lím (2x–1) = 2·(–3)–1 = –7;
x3
x  3
x (  )
5–x si x  3
lím
lím
x 5 f(x)= x5 (5–x)=5–5=0;
x (  )
1 si x  0
lím f(x) = lím 1 = 1;
x (  )
x2+1 si x>0
f(x)=
x  3
lím f(x) = xlím

(  ) (2x–1)= –
lím f(x) = xlím

(  ) (5–x) = –
lím f(x) = xlím
(  ) 1 = 1
x  3
2
lím
lím 2
x 5 f(x)= x 5 (x +1) = 5 +1 = 26;
2
lím f(x) = xlím
(  ) (x +1) = + 
x (  )
x2 – 2 si x<2 lím
f(x) = lím
(x2–2) =(–3)2–2=7;
x  3
x  3
x
si x>2
2
lím f(x) = xlím
(  ) (x –2)=+ 
x (  )
lím
lím
x 5 f(x)= x 5 x = 5;
lím f(x) = xlím
(  ) x = + 
x (  )
Ejercicio 19: Calcula, en cada caso el valor de k para que la función f(x) sea continua en todo  .
x2 – 4
si x  3
a) f(x)=
6–
x
2
x2  x
x
si x<2
b) f(x)=
x+k
c) f(x)=
x2 +kx
si x>3
si x  2
k
x=0
Solución:
Para que x sea continua en x = 3
 lím
f(x) = lím
f(x)
x 3
x 3
lím f(x)= lím (x+k) = 3+k
x 3
x 3

Para que x sea continua en x = 3
k=2
6–
x
2
si x<2
si x  0
5 = 3+k


lím f(x)= lím (x2–4) = 9–4 = 5;
x 3
x 3
k=2
lím f(x)= lím 6 – x = 6 – 2 = 5;
x 2
x 2
2
2
si
b) f(x)=
lím f(x)= lím (x2 +kx) = 4+2
x 2
x 2
si x  2
x2 +kx
Para que x sea continua en x=2  lím
f(x) = lím
f(x)  5=4+2k  k=1/2
x 2 
x 2 
x2  x
x
2
x x  1 lím
lím
lím x  x = lím
= x0 (x+1) = 1;
x  0 f(x)= x0
x0
x
x
si x  0
c) f(x)=
k
si x=0
Para que x sea continua en x=0  lim f(x) =f(0)=k  1=k  k=1
x 0
Ejercicio 20: Estudia la continuidad de estas funciones:
2–x si x<1
–x–1 si –1  x
a) f(x)=
b) f(x)=
1–x2
si –1<x<1
1
x
si x  1
2–x
si x<1
1
x
si x  1
x–1 si x  1
Solución:
lím f(x)= lím (2–x) = 2–1 = 1;
x 1
x 1
a) f(x)=
lím f(x)= lím 1 = 1 = 1 ;
f(1)=1
x1
x1
x 1
Para que x sea continua en x=1  lím
f(x) = lím
f(x) = f(1)  f continua en  .
x 1
x 1
–x–1
b) f(x)= 1–x2
x–1
si –1  x
si –1<x<1 ;
lím f(x)= lím lim (–x–1)= – ( –1) –1=0
x1
x  1
lím f(x)= lím (1–x2)=1– (–1)2=0
x1
x  1
si x  1
Como f(–1)=0= lím
f(x)= lím
f(x) 
x  1
x  1
lím f(x)= lím (1–x2) = 1–1 = 0;
x1
x 1
f continua en x=–1
lím f(x)= lím (x–1) = 1–1 = 0 y f(1) = 1–1 = 0 
x 1
x 1
Como f(1)=0= lím
f(x) = lím
f(x)  f continua en x=1  f continua en todo  .
x 1
x 1