Resumen Temario

UNED
Unidad Didáctica I:
Modelos probabilísticos
discretos
Primer tema de la asignatura de Estadística del Grado en Ingeniería
Informática
25/05/2018
Modelo matemático del azar
Consideremos A un acontecimiento de un experimento aleatorio. Hacemos N veces el
experimento y obtenemos n(A) veces el resultado A, entonces
n(A)
N
se aproxima a un valor fijo
para N grande: P(A) probabilidad empírica de A.
Propiedades:
 0 ≤ n(A) ≤ N ⇒ 0 ≤ P(A) ≤ 1
 Si A ocurre siempre ⇒ n(A) = N ⇒ P(A) = 1
 Si A y B son acontecimientos que no puede ocurrir simultáneamente ⇒ n(A ∪ B) =
n(A) + n(B) ⇒ P(A ∪ B) = P(A) + P(B)
Experimentos aleatorios
Los experimentos aleatorios cumplen:
1) No conocemos de antemano su resultado
2) Sus resultados posibles están bien determinados de antemano (espacio muestral, Ω)
3) Puede repetirse en idénticas condiciones tantas veces como queramos
Operaciones




Unión ⇒ 𝐴 ∪ 𝐵
Intersección ⇒ 𝐴 ∩ 𝐵
Complementario ⇒ 𝐴𝑐
Diferencia ⇒ 𝐴 − 𝐵 = 𝐴 ∩ 𝐵𝑐 = 𝐴\𝐵
Sucesos
 Sucesos incompatibles ⇒ Dos sucesos 𝐴 y 𝐵 son incompatibles si cumplen 𝐴 ∩ 𝐵 = ∅
 Suceso seguro ⇒ Aquel que se cumple siempre ⇒ 𝑃(Ω) = 1
 Suceso imposible ⇒ Aquel que no se cumple nunca ⇒ 𝑃(∅) = 0
Propiedades de la probabilidad
 Probabilidad del suceso complementario ⇒ Si 𝐴 es un suceso, se cumple 𝑃(𝐴) +
𝑃(𝐴𝑐 ) = 𝑃(Ω) = 1 ⇒ 𝑃(𝐴𝑐 ) = 1 − 𝑃(𝐴)
 Probabilidad de la diferencia ⇒ 𝐴 y 𝐵 son dos sucesos ⇒ 𝑃(𝐴 − 𝐵) = 𝑃(𝐴) −
𝑃(𝐴 ∩ 𝐵)
 Probabilidad de la unión de dos sucesos ⇒ Probabilidad de que suceda 𝐴 o suceda
𝐵 ⇒ 𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵)
 Probabilidad de monotonía ⇒ Si 𝐵 ⊂ 𝐴, entonces 𝑃(𝐵) ≤ 𝑃(𝐴)
 Desigualdad de Boole ⇒ Dados 𝑛 sucesos 𝐴𝑖 1 ≤ 𝑖 ≤ 𝑛 ⇒ 𝑃(⋃𝑛𝑖=1 𝐴𝑖 ) ≤ ∑𝑛𝑖=1 𝑃(𝐴𝑖 ).
Cuando 𝐴1 ∩ 𝐴2 ∩ … ∩ 𝐴𝑛 = ∅ → Tendremos la igualdad
Asignación de probabilidades
La probabilidad de cualquier suceso 𝐴 es la suma de las probabilidades de los sucesos simples
{𝜔}:
𝑃(𝐴) = ∑ 𝑃(𝜔)
𝜔∈𝐴
donde 𝑃(𝜔) tiene que cumplir:
0 ≤ 𝑃(𝜔) ≤ 1,
∑𝜔∈Ω 𝑃(𝜔) = 1
Regla de Laplace
Si todos los casos posibles son equiprobables, la probabilidad de un suceso es igual al cociente
entre el nº de casos favorables y el nº de casos posibles
𝑃(𝐴) =
𝐶𝑎𝑠𝑜𝑠 𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠
𝐶𝑎𝑠𝑜𝑠 𝑝𝑜𝑠𝑖𝑏𝑙𝑒𝑠
La elección del espacio muestral influye en el posterior cálculo de probabilidades.
Combinación sin repetición de 𝒏 objetos tomados de 𝒌 en 𝒌
Es una agrupación de 𝑘 objetos elegidos entre los 𝑛 posibles sin repetición alguna. Se calcula
mediante la fórmula:
𝑛!
𝑛
𝐶𝑛,𝑘 =
=( )
𝑘! × (𝑛 − 𝑘)!
𝑘
Variación sin repetición de 𝒏 objetos tomados de 𝒌 en 𝒌
Se trata de una agrupación alineada en recta (en fila) de 𝑘 objetos elegidos entre los 𝑛
disponibles sin repetición alguna. Se calcula mediante la fórmula:
𝑉𝑛,𝑘 =
𝑛!
(𝑛 − 𝑘)!
Variación con repetición de 𝒏 objetos tomados de 𝒌 en 𝒌
Es una agrupación alineada recta (en fila) de 𝑘 objetos elegidos entre los 𝑛 disponibles. En este
caso, los objetos se pueden repetir hasta 𝑘 veces. Se calcula mediante la fórmula:
𝑉𝑅𝑛,𝑘 = 𝑛𝑘
Permutación sin repetición de 𝒏 objetos
Es una agrupación alineada recta (en fila) de todos los objetos disponibles sin repetición
alguna. Es equivalente a una variación de 𝑛 objetos tomados de 𝑛 en 𝑛. Se calcula mediante la
fórmula:
𝑃𝑛 = 𝑛!
Cálculo por el complementario
Cuando la probabilidad que queremos sacar es una unión (disyunción) de dos elementos
(𝐶 = 𝐴 ∪ 𝐵, 𝑃(𝐶)), la cosa se complica. Entonces es preferible calcular su complementario
(𝑃(𝐶 𝑐 )) y después sacar su probabilidad (𝑃(𝐶) + 𝑃(𝐶 𝑐 ) = 1 ⇒ 𝑃(𝐶) = 1 − 𝑃(𝐶 𝑐 ))
Modelos dinámicos
Cuando tenemos un experimento compuesto por dos subexperimentos aleatorios, entonces
los llamaremos dinámicos.
Probabilidades condicionadas
Si 𝐴 y 𝐵 son dos sucesos, con 𝑃(𝐴) > 0, la probabilidad de 𝐵 condicionada por 𝐴 es:
𝑃(𝐵|𝐴) =
𝑃(𝐴 ∩ 𝐵)
𝑃(𝐴)
Propiedades
 𝑃(𝐴|𝐴) = 1
 𝑃(𝐵𝑐 |𝐴) = 1 − 𝑃(𝐵|𝐴)
 𝑃(𝐵1 ∪ 𝐵2 |𝐴) = 𝑃(𝐵1 |𝐴) + 𝑃(𝐵2 |𝐴)
De la fórmula de la probabilidad condicionada se saca:
𝑃(𝐵|𝐴) =
𝑃(𝐴 ∩ 𝐵)
⇒ 𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴)𝑃(𝐵|𝐴)
𝑃(𝐴)
Diagrama de árbol
 Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada
una de las posibilidades, acompañada de su probabilidad
 En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas
ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un
posible final del experimento (nudo final)
 Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo
ha de dar 1
Formula de la probabilidad total
𝑛
𝑃(𝐴) = ∑ 𝑃(𝐵𝑖 )𝑃(𝐴|𝐵𝑖 )
𝑖=1
Fórmula de Bayes
𝑃(𝐴𝑗 |𝐵) =
𝑃(𝐴𝑗 )𝑃(𝐵|𝐴𝑗 )
𝑛
∑𝑖=1 𝑃(𝐴𝑖 )𝑃(𝐵|𝐴𝑖 )
=
𝑃(𝐴𝑗 )𝑃(𝐵|𝐴𝑗 )
𝑃(𝐵)
Sucesos independientes
Dos sucesos serán independientes si se cumple que:
𝑃(𝐴 ∩ 𝐵) = 𝑃(𝐴)𝑃(𝐵) ⇒ 𝑃(𝐵|𝐴) = 𝑃(𝐵)
Los sucesos 𝐴𝑖 , 1 ≤ 𝑖 ≤ 𝑛, son independientes si cualquiera que sean 𝑘, 2 ≤ 𝑘 ≤ 𝑛, y los 𝑘
sucesos de la família 𝐴𝑖1 , … , 𝐴𝑖𝑘 , se cumple:
𝑃(𝐴𝑖1 ∩ 𝐴𝑖2 ∩ … ∩ 𝐴𝑖𝑘 ) = 𝑃(𝐴𝑖1 )𝑃(𝐴𝑖2 ) … 𝑃(𝐴𝑖𝑘 )
La probabilidad de cualquier intersección ha de ser igual al producto de las probabilidades
Si 𝑛 = 3: 𝐴1 , 𝐴2 , 𝐴3 ⇒ Podemos crear 3 parejas de sucesos (𝑘 = 2) y un trío (𝑘 = 3) y las
condiciones de independencia son:
 𝑘 = 2:
o
o
o
 𝑘=3
o
𝑃(𝐴1 ∩ 𝐴2 ) = 𝑃(𝐴1 )𝑃(𝐴2 )
𝑃(𝐴1 ∩ 𝐴3 ) = 𝑃(𝐴1 )𝑃(𝐴3 )
𝑃(𝐴2 ∩ 𝐴3 ) = 𝑃(𝐴2 )𝑃(𝐴3 )
𝑃(𝐴1 ∩ 𝐴2 ∩ 𝐴3 ) = 𝑃(𝐴1 )𝑃(𝐴2 ) 𝑃(𝐴3 )
Propiedades
 Si 𝐴𝑖 , 1 ≤ 𝑖 ≤ 𝑛 son sucesos independientes, también lo son sus complementarios y
cualquier colección que obtengamos sustituyendo algunos de los 𝐴𝑖 por sus
complementarios
 Si tres sucesos son independientes, el suceso que resulta de operar dos de ellos es
independiente del tercero
 La independencia de sucesos es particularmente favorable para emplear el método de
cálculo por el complementario
Cálculo de la unión de 𝒏 sucesos independientes
Tenemos que le complementario es 𝑃([⋃𝑛𝑖=1 𝐴𝑖 ]𝑐 ) = 𝑃(⋂𝑛𝑖=1 𝐴𝑐𝑖 )
Como son independientes ⇒ 𝑃(⋂𝑛𝑖=1 𝐴𝑐𝑖 ) = 𝑃(𝐴1𝑐 ) … 𝑃(𝐴𝑐𝑛 ) = (1 − 𝑃(𝐴1 )) … (1 − 𝑃(𝐴𝑛 ))
Conclusión: 𝑃(⋃𝑛𝑖=1 𝐴𝑖 ) = 1 − ∏𝑛𝑖=1(1 − 𝑃(𝐴𝑖 ))
Experimentos independientes
La independencia de los subexperimentos proporciona un método general para construir
espacios probabilísticos como producto de los asociados a cada experimento.
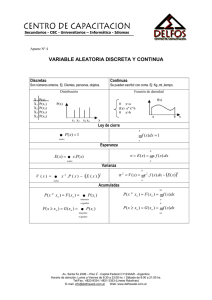
Variables aleatorias discretas
Aplicación/Función ⇒ Concepto matemático para describir algo que asocia un nº a cada
elemento de un conjunto.
Una variable aleatoria, 𝑋, definida sobre un espacio de probabilidad (Ω, P) es una función
X: Ω → ℝ
Si 𝑋 es una variable aleatoria ⇒ {𝑋 = 𝑥} representa a los sucesos 𝜔 tales que 𝑋(𝜔) = 𝑥:
{𝑋 = 𝑥} = {𝜔|𝑋(𝜔) = 𝑥} = 𝑋 −1 (𝑥)
Indicador de un suceso 𝑨 ⇒ Nos dice que si ocurre = 1 si no 0:
1
𝐼𝐴 (𝜔) = {
0
𝑠𝑖 𝜔 ∈ 𝐴
𝑠𝑖 𝜔 ∉ 𝐴
Racha ⇒ Serie maximal de resultados iguales
Distribución de una variable
Distribución de probabilidad 𝒑(𝒙) ⇒ Función que nos enseña el modo de repartirse la
probabilidad entre los valores posibles de la variable
Distribución de una función 𝒀 = 𝒈(𝑿) ⇒ Consideremos una variable aleatoria 𝑋. Cualquier
función 𝑌 = 𝑔(𝑋) es una variable aleatoria, porque asigna un valor a cada resultado posible.
Valor esperado de una variable
Valor esperado (esperanza matemática o media) ⇒ Promedio de los valores que toma la
variable ponderado por la probabilidad con que toma cada valor (“centro de gravedad de la
distribución”). 𝑋 es una variable aleatoria discreta, su esperanza 𝐸{𝑋}
𝐸{𝑋} = ∑ 𝑥𝑃(𝑋 = 𝑥)
𝑥∈𝑋(Ω)
Valor esperado de una función de una variable aleatoria ⇒ 𝑋: variable aleatoria; 𝑌 = 𝑔(𝑋)
función de 𝑋. Podemos promediar respecto a los valores de 𝑋 en lugar de hallar la función de
probabilidad de 𝑌, mediante:
𝐸{𝑌} = 𝐸{𝑔(𝑋)} = ∑ 𝑔(𝑥)𝑃(𝑋 = 𝑥)
𝑥∈𝑋(Ω)
Esperanza de una función lineal ⇒ Si 𝑌 = 𝑎𝑋 + 𝑏 ⇒ 𝐸{𝑎𝑋 + 𝑏} = 𝑎𝐸{𝑋} + 𝑏
Varianza y momentos de una variable
Dada una variable X, los valores esperados de las funciones de la forma 𝑔(𝑥) = 𝑥 𝑚 se
denominan momentos de 𝑋. Así:
 𝜇1 = 𝐸{𝑋} momento de primer orden
 𝜇2 = 𝐸{𝑋 2 } momento de segundo orden
 𝜇𝑟 = 𝐸{𝑋 𝑟 } momento de orden 𝑟
Desviación cuadrática respecto a la media ⇒ Mide el error que cometemos al sustituir un
valor posible, 𝑥, por 𝐸{𝑋}
𝑔(𝑋) = (𝑋 − 𝐸{𝑋})2
Varianza de 𝑿 ⇒ Dispersión promedio de los valores de 𝑋 respecto de 𝐸{𝑋}
𝜎𝑋2 = 𝐸{(𝑋 − 𝐸{𝑋})2 } = 𝐸{𝑋 2 } − (𝐸{𝑋})2
La varianza cumple:
2
 𝜎𝑋+𝑏
= 𝜎𝑋2 invariante por traslación 𝑋 → 𝑋 + 𝑏
2
 𝜎𝑎𝑋+𝑏
= 𝑎2 𝜎𝑋2 por cambio de escala 𝑋 → 𝑎𝑋
Desigualdad de Chebyshev
Consideremos una variable 𝑋 de media 𝜇 y varianza 𝜎𝑋2 . La probabilidad de que 𝑋 tome valores
más alejados de la media 𝜇 que un nº dado 𝑎 > 0, es estimar la probabilidad del suceso
|𝑋 − 𝜇| > 𝑎:
𝜎𝑋2
𝑃(|𝑋 − 𝜇| > 𝑎) ≤ 2
𝑎
2
2
 Si 𝑎 = 𝜎𝑋 → 𝑃 ≤ 1
 Si 𝑎2 = 2𝜎𝑋2 → 𝑃 ≤ 0.5
“normalizando” la probabilidad 𝜀 = 𝜎𝑋 𝑎 :
𝑃(|𝑋−, 𝑢| > 𝜀) ≤
1
𝑎2
donde para 𝑎 ≤ 1 dará 𝑃 ≥ 1 (solución trivial) y solución no trivial para 𝑎 > 1
Entropía de una variable aleatoria
La entropía asociada a una variable aleatoria 𝑋 es el valor esperado de la esperanza de
– 𝑙𝑜𝑔 𝑝(𝑋), donde 𝑝(𝑥) es la función de probabilidad de 𝑋. La entropía de 𝑋 se representa por
𝐻(𝑋).
1
1
𝐻(𝑋) = 𝐸 {log 2
= − ∑ 𝑝(𝑥) log 𝑝(𝑥)
} = ∑ 𝑝(𝑥) log
𝑝(𝑋)
𝑝(𝑥)
𝑥∈𝑋(Ω)
𝑥∈𝑋(Ω)
La entropía de una variable aleatoria 𝑋 es una medida de la incertidumbre asociada a ella. Si
𝑙𝑜𝑔 es base 2 → [𝐻] = 𝑏𝑖𝑡
Distribución de Bernoulli
Tras un experimento aleatorio sólo nos interesa saber si cierto suceso ha ocurrido o no, por
ejemplo:, tirar una moneda al aire y mirar si sale cara o cruz.
Solo hay un parámetro, 𝑝, probabilidad de que salga o no:
𝑃(𝑋 = 0) = 1 − 𝑝
𝑃(𝑋 = 1) = 𝑝
Valor esperado 𝜇 = 𝐸{𝑋} = 𝑝
Momento a segundo orden 𝜇2 = 𝐸{𝑋 2 } = 𝑝
Varianza 𝜎𝑋2 = 𝐸{𝑋 2 } − (𝐸{𝑋})2 = 𝑝(1 − 𝑝)
Distribución binomial
Mirar tras realizar 𝑛 pruebas si ha ocurrido el suceso. Por ejemplo, lanzar 𝑛 veces una moneda
de probabilidad 𝑝 de que salga cara (veces que ha salido cara de la 𝑛 tiradas)
Depende de dos variables: 𝑛, 𝑝
Probabilidad de que el suceso pase 𝒌 veces:
𝑃(𝑋 = 𝑘) = (𝑛𝑘)𝑝𝑘 (1 − 𝑝)𝑛−𝑘 , para 𝑘 = 0,1, … , 𝑛
Si 𝑛 = 1 recuperamos la distribución de Bernoulli
Media y varianza:
 𝜇 = 𝑛𝑝
 𝜎2 = 𝑛𝑝(1 − 𝑝)
Distribución geométrica
Seria lanzar repetidas veces una moneda hasta que sale la primera cara y contar el número de
lanzamientos (𝑘).
Si 𝑝 es la probabilidad de que salga cara, y hemos sacado 𝑘 cruces seguidas:
𝑃(𝑋 = 𝑘) = 𝑝(1 − 𝑝)𝑘−1 , si 𝑘 = 1,2,3, …
Media y varianza:
1
 𝜇=𝑝
 𝜎𝑋2 =
1−𝑝
𝑝2
Al realizar cálculos con las distribuciones geométricas, en muchas ocasiones es preciso sumar
una serie geométrica, recordemos que la fórmula de la suma de una serie geométrica de
razón 𝒓 es
∞
𝑟
∑
𝑟𝑘 =
, 𝑣á𝑙𝑖𝑑𝑎 𝑠𝑖 |𝑟| < 1
1−𝑟
𝑘=1
Distribución de Poisson
Cuando contamos cuántas veces ha ocurrido un suceso que tiene un probabilidad muy
pequeña de que ocurra en un intervalo de tiempo; por ejemplo los procesos de desintegración
radiactiva
Depende del parámetro 𝜆 > 0, y la función de probabilidad es:
𝑃(𝑋 = 𝑘) = 𝑒 −𝜆
𝜆𝑘
𝑘!
Media y varianza: 𝜇 = 𝜎𝑋2 = 𝜆
Cálculo recursivo
Tanto el cálculo de la distribución binomial como la de Poisson contienen factoriales en la
fórmula de la probabilidad
El cálculo del factorial no es aconsejable en programación, por lo que se recurre al método
recursivo
Se trata de calcular el próximo valor a partir del anterior
Binomial
𝑃(𝑋 = 𝑘 + 1) =
𝑝 𝑛−𝑘
𝑃(𝑋 = 𝑘)
1−𝑝𝑘+1
Posisson
𝑃(𝑋 = 𝑘 + 1) =
𝜆
𝑃(𝑋 = 𝑘)
𝑘+1
Vectores aleatorios discretos
Vectores aleatorios discretos ⇒ Vectores obtenidos a partir de variables discretas
(𝑋1 , 𝑋2 , … , 𝑋𝑛 ) definidas sobre un mismo espacio de probabilidad.
Se obtienen de medir simultáneamente varias magnitudes de un mismo elemento.
Distribución conjunta de un vector aleatorio
Función de probabilidad conjunta del vector (𝑋, 𝑌):
𝑝(𝑖, 𝑗) = 𝑃(𝑋 = 𝑖, 𝑌 = 𝑗),
𝑖 ∈ 𝑋(𝛺),
Cualquier conjunto o matriz de números (𝑝(𝑖, 𝑗)),
distribución conjunta siempre que cumpla:
𝑖 ∈ 𝑋(𝛺),
𝑗 ∈ 𝑌(𝛺)
𝑗 ∈ 𝑌(𝛺), define una
𝑝(𝑖, 𝑗) ≥ 0 y ∑𝑖∈𝑋(Ω) ∑𝑗∈𝑌(Ω) 𝑝(𝑖, 𝑗) = 1
Cálculo de probabilidades a partir de la distribución conjunta
 Cálculo de la probabilidad mediante condiciones
 Dado un vector (𝑋, 𝑌), y alguna restricción sobre ellas, 𝐵, su probabilidad:
𝑃((𝑋, 𝑌) ∈ 𝐵) = ∑ 𝑃(𝑋 = 𝑖, 𝑌 = 𝑗)
(𝑖,𝑗)∈𝐵
Distribuciones marginales
Cuando sólo ponemos restricción en una de las variables:
𝑃(𝑋 = 𝑖) = ∑ 𝑃(𝑋 = 𝑖, 𝑌 = 𝑗) ,
𝑖 ∈ 𝑋(Ω) (𝑓𝑖𝑗𝑎𝑚𝑜𝑠 𝑋)
𝑗∈𝑌(Ω)
𝑃(𝑌 = 𝑗) = ∑ 𝑃(𝑋 = 𝑖, 𝑌 = 𝑗) ,
𝑗 ∈ 𝑌(Ω) (𝑓𝑖𝑗𝑎𝑚𝑜𝑠 𝑌)
𝑖∈𝑋(Ω)
El conjunto {𝑃(𝑋 = 𝑖)}𝑖∈𝑋(𝛺) define la distribución unidimensional de 𝑋. El conjunto
{𝑃(𝑌 = 𝑗)}𝑗∈𝑌(𝛺) define la distribución unidimensional de 𝑌.
Definiendo la distribución 𝑃(𝑋, 𝑌) en tabla, 𝑃(𝑋 = 𝑖) es la suma de las probabilidades de la fila
𝑖-ésima (para 𝑃(𝑌 = 𝑗) para la columna 𝑗-ésima).
Valores esperados en una distribución conjunta
Por extensión del caso unidimensional, la esperanza matemática de una función del vector
aleatorio, 𝑓(𝑋, 𝑌), se define por:
𝐸{𝑓(𝑋, 𝑌)} = ∑
∑ 𝑓(𝑖. , 𝑗)𝑃(𝑋 = 𝑖, 𝑌 = 𝑗)
𝑖∈𝑋(Ω) 𝑗∈𝑌(Ω)
Valor esperado de la suma de dos variables
Cualesquiera que sean las variables 𝑋1 , 𝑋2 , … , 𝑋𝑛 , se cumple:
𝐸{𝑋1 + 𝑋2 + ⋯ + 𝑋𝑛 } = 𝐸{𝑋1 } + 𝐸{𝑋2 } + ⋯ + 𝐸{𝑋𝑛 }
Covarianza de dos variables
La covarianza entre dos variables es un parámetro de la distribución conjunta que mide la
variación simultánea de 𝑋 e 𝑌:
𝜎𝑋,𝑌 = 𝐸{(𝑋 − 𝐸{𝑋})(𝑌 − 𝐸{𝑌})}
que no es más que la esperanza de la función
𝑓(𝑋, 𝑌) = (𝑋 − 𝐸{𝑋})(𝑌 − 𝐸{𝑌})
Coeficiente de correlación
𝜌𝑋,𝑌 =
𝜎𝑋,𝑌
√𝜎𝑋2 𝜎𝑌2
con −1 ≤ 𝜌𝑋,𝑌 ≤ 1. Nos indica el grado de ajuste lineal entre las variables, de tal manera que
si 𝜌𝑋,𝑌 → 0 las variables están descorrelacionadas (incorreladas).
Propiedades del valor esperado
El valor esperado 𝐸 (esperanza) es un operador lineal de 𝑋 e 𝑌:
𝐸{𝑎𝑋 + 𝑏𝑌} = 𝑎𝐸{𝑋} + 𝑏𝐸{𝑌}
Aplicando la linealidad la covarianza queda:
𝜎𝑋,𝑌 = 𝐸{𝑋𝑌} − 𝐸{𝑋}𝐸{𝑌}
Distribuciones condicionadas
De la definición de probabilidad condicionada, se sigue que la probabilidad del suceso 𝑋 (para
todos sus valores) condicionada a que sabemos que 𝑌 = 𝑦
𝑃(𝑋 = 𝑥|𝑌 = 𝑦) =
𝑃(𝑋 = 𝑥, 𝑌 = 𝑦)
,
𝑃(𝑌 = 𝑦)
𝑥 ∈ 𝑋(Ω)
También se puede interpretar de un modo dinámico de dos sorteos, primer el sorteo de 𝑌
(respecto a la distribución marginal) y después el valor de 𝑋 respecto a la distribución marginal
de 𝑌.
La esperanza matemática de la distribución 𝑋|𝑌 = 𝑗
𝐸{𝑋|𝑌 = 𝑗} = ∑ 𝑖𝑃(𝑋 = 𝑖|𝑌 = 𝑗)
𝑖∈𝑋(Ω)
herramienta muy útil ya que reduce el problema a otros menores.
Variables aleatorias independientes
Dos variables aleatorias 𝑋, 𝑌 definidas sobre un mismo espacio de probabilidad son
independientes si se cumple
𝑃(𝑋 = 𝑖, 𝑌 = 𝑗) = 𝑃(𝑋 = 𝑖)𝑃(𝑌 = 𝑗)
para cada 𝑖 ∈ 𝑋(𝛺), 𝑗 ∈ 𝑌(𝛺). La independencia de 𝑋 e 𝑌 es una propiedad de su distribución
conjunta.
La independencia de dos variables significa que saber que 𝑌 = 𝑗 no altera la probabilidad
marginal de 𝑋, cualquiera que sea 𝑌
La condición de independencia de dos sucesos es simétrica: si 𝑋 es independiente de 𝑌, 𝑌 será
también independiente de 𝑋
Si dos variables 𝑋 e 𝑌 son independientes, cualquier suceso 𝐴 definido por una condición
sobre 𝑋 es independiente de cualquier suceso 𝐵 definido por una condición sobre 𝑌
𝑃(𝑋 ∈ 𝐴, 𝑌 ∈ 𝐵) = 𝑃(𝑋 ∈ 𝐴)𝑃(𝑌 ∈ 𝐵)
Así mismo, la propiedad de las variables independientes implica que dos funciones de 𝑋 e 𝑌,
𝑓(𝑋) y 𝑔(𝑌), también son independientes.
Conjuntos y sucesiones de variables independientes
Las variables 𝑋1 , 𝑋2 , … , 𝑋𝑛 , son independientes si se verifica
𝑛
𝑃(𝑋1 = 𝑥1 , 𝑋2 = 𝑥2 , … , 𝑋𝑛 = 𝑥𝑛 ) = ∏ 𝑃(𝑋𝑘 = 𝑥𝑘 )
𝑘=1
cualquiera que sean 𝑥𝑘 ∈ 𝑋𝑘 (𝛺), 1 ≤ 𝑘 ≤ 𝑛.
Para que sean independientes lo tienen que ser dos a dos, tres a tres, cuatro a cuatro, etc.
Generalizando a sucesiones infinitas ⇒ Las variables de una sucesión {𝑋𝑛 }∞
𝑛=1 son
independientes si las variables de cualquier subconjunto finito lo son.
Esperanza del producto de variables independientes
Si dos variables, 𝑋 e 𝑌, son independientes, la esperanza y el producto de las variables
conmutan y se verifica
𝐸{𝑋𝑌} = 𝐸{𝑋}𝐸{𝑌}
Si 𝑓 y 𝑔 son funciones de las variables 𝑋, 𝑌 independientes, entonces 𝑓(𝑋) y 𝑔(𝑌) son
independientes y cumple
𝐸{𝑓(𝑋)𝑔(𝑌)} = 𝐸{𝑓(𝑋)}𝐸{𝑔(𝑌)}
De manera general ⇒ Si 𝑋𝑖 , 1 ≤ 𝑖 ≤ 𝑛, son independientes y 𝑓𝑖 , 1 ≤ 𝑖 ≤ 𝑛, son funciones, las
variables 𝑓𝑖 (𝑋𝑖 ) son independientes y se cumple:
𝑘
𝑘
𝐸 {∏ 𝑓𝑖 (𝑋𝑖 ) } = ∏ 𝐸{𝑓𝑖 (𝑋𝑖 )}
𝑖=1
𝑖=1
Varianza de la suma de variables independientes
Si 𝑋 e 𝑌 son variables independientes con varianzas finitas, la varianza de la suma de las
variables es igual a la suma de las varianzas:
2
𝜎𝑋+𝑌
= 𝜎𝑋2 + 𝜎𝑌2
Generalizando ⇒ Si 𝑋𝑖 , 1 ≤ 𝑖 ≤ 𝑛, son independientes y tienen varianzas finitas, se cumple
𝜎𝑋21 +𝑋2 +···+𝑋𝑛 = 𝜎𝑋21 + 𝜎𝑋22 + ⋯ + 𝜎𝑋2𝑛
Leyes de los grandes números
Consideremos una serie de pruebas repetidas independientes de un mismo experimento que
modelamos en una sucesión 𝑋1 , 𝑋2 , … de variables aleatorias independientes. Todas con igual
distribución y media y varianza 𝜇, 𝜎 2 .
Si 𝑋’𝑛 es la media aritmética de los valores observados en las 𝑛 primeras pruebas
𝑋1 + 𝑋2 + ⋯ + 𝑋𝑛
𝑋𝑛′ =
𝑛
entonces si 𝑛 → ∞
lim 𝑃(|𝑋𝑛′ − 𝜇| > 𝜀) = 0
𝑛→∞
la probabilidad de que 𝑋’𝑛 se aleje de la media 𝜇 en más de una cantidad 𝜀 irá a cero así como
aumentamos 𝑛.
UNED
Unidad Didáctica II:
Modelos probabilísticos
continuos
Segundo tema de la asignatura de Estadística del Grado en Ingeniería
Informática
26/05/2018
Puntos al azar en el continuo
Para el caso del discreto, la regla de Laplace que nos proporcionaba la probabilidad venia dado
por:
𝑐𝑎𝑠𝑜𝑠 𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠
𝑐𝑎𝑠𝑜𝑠 𝑝𝑜𝑠𝑖𝑏𝑙𝑒𝑠
En el continuo, la probabilidad es la relación entre el tamaño geométrico de las regiones
formadas por los puntos “favorables” y los “posibles”.
Probabilidad geométrica ⇒ Si se elige un punto 𝑃 al azar en un conjunto 𝐴 de algun espacio
euclideo ℝ, ℝ2 , ℝ3 , etc, la probabilidad de que el punto elegido pertenezca a 𝐵 ⊂ 𝐴 es
𝑃(𝑃 ∈ 𝐵) =
𝑚𝑒𝑑𝑖𝑑𝑎(𝐵)
𝑚𝑒𝑑𝑖𝑑𝑎(𝐴)
La probabilidad geométrica nos deja elegir la dimensión para plantear el problema.
Función de densidad de una variable aleatoria
La función densidad de probabilidad cumple:
𝑓(𝑥) ≥ 0
∞
∫ 𝑓(𝑡)𝑑𝑡 = 1
−∞
La probabilidad de un suceso 𝑋 ∈ 𝐼, dónde 𝐼 es un intervalo, se obtiene mediante la integral
𝑃(𝑋 ∈ 𝐼) = ∫ 𝑓(𝑡)𝑑𝑡
𝐼
Interpretación gráfica
El área total de la función densidad de probabilidad es igual a 1.
El área por debajo de la función densidad de probabilidad representa la probabilidad.
El área de una región equivale a la probabilidad de obtener un resultado de dicho intervalo.
𝑏
𝑃(𝑋 ∈ (𝑎, 𝑏)) = ∫ 𝑓(𝑡)𝑑𝑡
𝑎
Valor esperado de una variable continua
La esperanza matemática o valor esperado de una variable 𝑋 con función de densidad 𝑓 es la
integral:
∞
𝐸{𝑋} = ∫ 𝑡𝑓(𝑡)𝑑𝑡
−∞
siempre que la integral sea finita
Si la integral es infinita, se dice que la variable no tiene valor medio.
Valor esperado de una función
Valor esperado de una función 𝑌 = 𝑔(𝑋)
∞
𝐸{𝑔(𝑋)} = ∫ 𝑔(𝑡)𝑓(𝑡)𝑑𝑡
−∞
donde 𝑔(𝑋) es la función de densidad de 𝑋
La varianza de 𝑋, se define como la esperanza de la función 𝑔(𝑋) = (𝑋 − 𝐸{𝑋})2
∞
𝜎𝑋2
= ∫ (𝑡 − 𝐸{𝑋})2 𝑓(𝑡)𝑑𝑡 = 𝐸{𝑋 2 } − (𝐸{𝑋})2
−∞
Función de densidad uniforme
Paradigma: elegir un punto al azar en un intervalo [𝑎, 𝑏]
1
𝑓(𝑥) = {𝑏 − 𝑎
0
 Esperanza ⇒ 𝐸{𝑋} =
𝑥 ∈ [𝑎. 𝑏]
𝑥 ∉ [𝑎. 𝑏]
𝑎+𝑏
2
𝑏2 +𝑎𝑏+𝑎 2
3
(𝑏−𝑎)2
 Momento a segundo orden ⇒ 𝐸{𝑋 2 } =
 Varianza ⇒ 𝜎𝑋2 = 𝐸{𝑋 2 } − (𝐸{𝑋})2 =
12
Función de densidad exponencial
Paradigma: Tiempo que tarda en desintegrarse un átomo de una masa de material radioactivo
o tiempo de funcionamiento de un dispositivo hasta que se avería.
0
𝑓(𝑥) = { −𝜆𝑥
𝜆𝑒
𝑥<0
𝑥≥0
Depende de un parámetro 𝜆 > 0 (si 𝜆 ↑ la exponencial decae más rápidamente)
1
 Esperanza ⇒ 𝐸{𝑋} = 𝜆
 Momento a segundo orden ⇒ 𝐸{𝑋 2 } =
1
𝜆2
1
 Varianza ⇒ 𝜎𝑋2 = 𝐸{𝑋 2 } − (𝐸{𝑋})2 = 𝜆2
Función de densidad normal
Definida por
𝑓(𝑥) =
1
√2𝜋𝜎
𝑒
−
(𝑥−𝜇)2
2𝜎2
Depende de dos parámetros: 𝜇 (media de distribución) y 𝜎 (𝜎 2 varianza)
Familia de distribuciones 𝒩(𝜇, 𝜎)
𝒩(0, 1) ⇒ Función de densidad con 𝜇 = 0 y 𝜎 = 1
Propiedades
 Si 𝑋 es una variable con distribucion 𝒩(𝜇, 𝜎) y 𝑎, 𝑏 ∈ ℝ, entonces 𝑎𝑋 + 𝑏 tiene
distribucion normal de media y varianza:
𝐸{𝑎𝑋 + 𝑏} = 𝑎𝐸{𝑋} + 𝑏 = 𝑎𝜇 + 𝑏
2
2
𝜎𝑎𝑋+𝑏
= 𝜎𝑎𝑋
= 𝑎2 𝜎𝑋2 = 𝑎2 𝜎 2
 Si 𝑋 tiene distribucion 𝒩(𝜇, 𝜎), la variable 𝑍 =
𝑋−𝜇
𝜎
tiene distribución 𝒩(0,1).
Funciones de distribución
La función de distribución, 𝐹(𝑥), en cada punto 𝑥, devuelve el valor de la probabilidad
acumulada en el intervalo (−∞, 𝑥] (lo que es la probabilidad de que la variable aleatoria 𝑋
tome valores menores o iguales a 𝑥) ⇒ 𝐹(𝑥) = 𝑃(𝑋 ≤ 𝑥) función de distribución de 𝑋.
Caracterización de las funciones de distribución
Toda función de distribución 𝐹 verifica:
 𝐹 es no decreciente ⇒ Si 𝑥 < 𝑥′, se tiene 𝐹(𝑥) ≤ 𝐹(𝑥 ′ )
 𝐹 es continua por la derecha
 Se cumple lim𝑥→∞ 𝐹(𝑥) = 1 y lim𝑥→−∞ 𝐹(𝑥) = 0
De la misma manera que si se cumplen las tres condiciones, entonces esta función 𝐹 es una
función de distribución.
La función de distribución es válida tanto para variable continua como discreta.
Variable continua ⇒ Variable 𝑋 continua con función densidad 𝑓(𝑥); la función de distribución
será:
𝑥
𝐹𝑋 (𝑥) = 𝑃(𝑋 ≤ 𝑥) = ∫ 𝑓(𝑡)𝑑𝑡
−∞
Función de distribución de una transformada
Dada 𝑋, variable aleatoria con funcion de distribucion 𝑔(𝑥), la función de distribución de
𝑌 = 𝑓(𝑋) será en el intervalo 𝐼 = (−∞, 𝑦]
𝐹𝑌 (𝑦) = 𝑃(𝑌 ≤ 𝑦) = 𝑃(𝑔(𝑋) ≤ 𝑦) = 𝑃(𝑋 ∈ 𝑔−1 (𝐼))
Transformaciones lineales
Conocemos la distribución de 𝑋 con función densidad 𝑓𝑋 (𝑥) y función de distribución 𝐹𝑋 (𝑥);
𝑌 = 𝑎𝑋 + 𝑏, 𝑎 > 0, entonces:
𝑦−𝑏
𝑦−𝑏
) = 𝐹𝑋 (
)
𝑎
𝑎
𝑑
𝑑
𝑦−𝑏
𝑑 𝑦−𝑏
𝑦−𝑏
1
𝑦−𝑏
𝐹𝑌′ (𝑦) =
𝐹𝑌 (𝑦) =
𝐹𝑋 (
)=
(
) 𝑓𝑋 (
) = 𝑓𝑋 (
)
𝑑𝑦
𝑑𝑦
𝑎
𝑑𝑦
𝑎
𝑎
𝑎
𝑎
𝐹𝑌 (𝑦) = 𝑃(𝑌 ≤ 𝑦) = 𝑃(𝑎𝑋 + 𝑏 ≤ 𝑦) = 𝑃 (𝑋 ≤
Funciones de densidad conjunta
Distribución bidimensional continua ⇒ Diremos que un vector aleatorio (𝑋, 𝑌) tiene
distribucion de probabilidad continua si existe una función 𝑓(𝑥, 𝑦), que denominaremos
función de densidad bidimensional conjunta (o función de densidad conjunta) tal que
𝑃(𝑋 ∈ 𝐼1 , 𝑌 ∈ 𝐼2 ) = ∬ 𝑓(𝑥, 𝑦)𝑑𝑦𝑑𝑥
𝐼1 ×𝐼2
También cumplirá entonces:
𝑃((𝑋, 𝑌) ∈ 𝐵) =
∬ 𝑓(𝑥, 𝑦)𝑑𝑦𝑑𝑥
(𝑥,𝑦)∈𝐵
𝑓(𝑥, 𝑦) será función de densidad conjunta si verifica:
 𝑓(𝑥, 𝑦) ≥ 0, para −∞ < 𝑥 < +∞, −∞ < 𝑦 < +∞
 𝑓(𝑥, 𝑦)𝑑𝑥𝑑𝑦 = 1
Funciones de densidad marginales
Si (𝑋, 𝑌) es un vector aleatorio con densidad conjunta 𝑓(𝑥, 𝑦), cada una de sus componentes
𝑋 e 𝑌 tienen distribución unidimensional continua que se calcula a partir de la conjunta
∞
∞
𝑓𝑋 (𝑥) = ∫−∞ 𝑓(𝑥, 𝑦)𝑑𝑦
𝑓𝑌 (𝑦) = ∫−∞ 𝑓(𝑥, 𝑦)𝑑𝑥
𝑓𝑋 (𝑥) y 𝑓𝑌 (𝑦), densidades marginales de 𝑋 e 𝑌.
En 𝑥 acumulamos toda la densidad de probabilidad que tienen los puntos (𝑥, 𝑦), con 𝑥 fijo e 𝑦
variable.
Para el cálculo de probabilidad para un intervalo 𝐵:
∞
𝑃(𝑋 ∈ 𝐵) = ∫ ∫ 𝑓(𝑥, 𝑦)𝑑𝑦𝑑𝑥 = ∫ 𝑓𝑋 (𝑥)𝑑𝑥
𝑥∈𝐵 −∞
𝑥∈𝐵
Funciones de densidad condicionadas
Si el vector (𝑋, 𝑌) tiene función de densidad conjunta 𝑓(𝑥, 𝑦), la función de densidad de la
variable condicionada 𝑌|𝑋 = 𝑥 es igual a
𝑓(𝑥, 𝑦)
𝑓𝑦|𝑥 (𝑦) = { 𝑓𝑋 (𝑥)
0
𝑠𝑖 𝑓𝑋 (𝑥) > 0
𝑠𝑖 𝑓𝑋 (𝑥) = 0
Independencia de dos valores
Independencia de valores ⇒ Si el vector (𝑋, 𝑌) tiene función de densidad conjunta 𝑓(𝑥, 𝑦),
decimos que las variables 𝑋 e 𝑌 son independientes si se cumple
𝑓(𝑥, 𝑦) = 𝑓𝑋(𝑥)𝑓𝑌(𝑦), para cada par (𝑥, 𝑦)
Modelos dinámicos continuos
De la función de densidad condicionada podemos sacar:
𝑓(𝑥, 𝑦) = 𝑓𝑋 (𝑥)𝑓(𝑦|𝑥)
Valores esperados y momentos
Si 𝑋 e 𝑌 son dos variables aleatorias con función de densidad conjunta 𝑓(𝑥, 𝑦), la esperanza
matematica de una funcion 𝑔(𝑥, 𝑦)
∞
∞
𝐸{𝑔(𝑋, 𝑌)} = ∫ ∫ 𝑔(𝑥, 𝑦)𝑓(𝑥, 𝑦)𝑑𝑦𝑑𝑥
−∞ −∞
supuesto que la integral exista.
Valor esperado de una función lineal
𝐸{𝑎𝑋 + 𝑏𝑌} = 𝑎𝐸{𝑋} + 𝑏𝐸{𝑌}
Valor esperado de funciones independientes ⇒ Si 𝑋 e 𝑌 son dos variables independientes y 𝑔
y ℎ son dos funciones medibles, 𝑔(𝑋) y ℎ(𝑋) son independientes y se cumple:
𝐸{𝑔(𝑋)ℎ(𝑌)} = 𝐸{𝑔(𝑋)}𝐸{ℎ(𝑌)}
Varianza y covarianza de un vector aleatorio
Varianza de una variable aleatoria 𝑿 𝐸{𝑔(𝑋)} con 𝑔(𝑋) = (𝑋 − 𝐸{𝑋})2
𝜎𝑋2 = 𝐸{(𝑋 − 𝐸{𝑋})2 }
Covarianza entre las variables 𝐗 e 𝐘 ⇒ Es el valor esperado de 𝑔(𝑋, 𝑌) = (𝑋 − 𝐸{𝑋})(𝑌 −
𝐸{𝑌})
𝐶𝑜𝑣𝑋𝑌 = 𝐸{(𝑋 − 𝐸{𝑋})(𝑌 − 𝐸{𝑌})}
 La covarianza mide la co-variacion de las variables
 Propiedad ⇒ 𝐶𝑜𝑣𝑋𝑌 = 𝐸{𝑋𝑌} − 𝐸{𝑋}𝐸{𝑌}
 Coeficiente de correlación ⇒ 𝜌𝑋,𝑌 =
𝐶𝑜𝑣𝑋𝑌
𝜎𝑋 𝜎𝑌
⇒ Nº adimensional que mide el grado de
asociación lineal entre 𝑋 e 𝑌.
 Si 𝜎𝑋,𝑌 = 0 ⇒ 𝜌𝑋𝑌 = 0, variables incorrelacionadas (⇍)
UNED
Unidad Didáctica III:
Muestreo aleatorio
Tercer tema de la asignatura de Estadística del Grado en Ingeniería
Informática
26/05/2018
Muestras aleatorias
Muestra ⇒ Datos obtenidos mediante la observación repetida del fenómeno o de fenómenos
relacionados
Supongamos que de una variable 𝑋 conocemos el tipo de distribución, pero no conocemos sus
parámetros. Para adquirir información sobre estos se realizan 𝒏 observaciones (repeticiones)
del experimento con 𝑥𝑖 valor observado 𝑖-esimo: (𝑥1 , 𝑥2 , … , 𝑥𝑛 ) muestra aleatoria de 𝑋.
Tamaño de la muestra es 𝑛.
Muestra aleatoria simple ⇒ Cuando las observaciones están formadas por repeticiones
independientes.
La inferencia estadística hace sus análisis y elabora previsiones en base a diversas funciones
calculadas a partir de los datos muestrales, cualquier función de los valores de la muestra se
denomina estadístico. Ejemplo: la media de la muestra
Estadístico → Función de los valores muestrales
Distribución de la muestra ⇒ Una muestra aleatoria simple, de tamaño 𝑛, de una variable
aleatoria 𝑋 es un vector aleatorio (𝑋1 , 𝑋2 , … , 𝑋𝑛 ) de variables independientes con la misma
distribución que 𝑋; si 𝑋 es discreta con función de probabilidad 𝑝(𝑥), la función de
probabilidad de la muestra será
𝑝(𝑥1 , … , 𝑥𝑛 ) = 𝑝(𝑥1 )𝑝(𝑥2 ) … 𝑝(𝑥𝑛 )
y si 𝑋 es continua con funcion de densidad 𝑓(𝑥), la función de densidad conjunta de la
muestra será
𝑓(𝑥1 , … , 𝑥𝑛 ) = 𝑓(𝑥1 )𝑓(𝑥2 ) … 𝑓(𝑥𝑛 )
Dos importantes razones teóricas avalan al muestreo aleatorio simple. La primera razón es la
disminución de la variabilidad conforme aumenta el tamaño de la muestra, sabemos que si la
variable 𝑋 tiene media 𝜇 y varianza 𝜎 2 , la media de la muestra, 𝑋̅,
̅𝑋̅̅𝑛̅ =
tiene media 𝜇 y varianza
𝜎2
,
𝑛
𝑋1 + 𝑋2 + ⋯ + 𝑋𝑛
𝑛
lo que significa que al aumentar el tamaño de la muestra la
variabilidad del estadístico media muestral disminuye y sus valores están más y más
concentrados alrededor del valor 𝜇, lo que nos hace esperar que ̅𝑋̅̅𝑛̅ sea un valor que permita
obtener buenas aproximación de 𝜇 si el tamaño de la muestra es suficientemente grande. Esta
observación tiene una importancia crucial, pues supone que podemos mejorar nuestro
conocimiento de un fenómeno mediante observaciones repetidas del mismo. La segunda
razón se basa en la ley de los grandes números y precisa que la media de la muestra converge
a la desconocida media de 𝑋 cuando 𝑛 → ∞.
Al aumentar el tamaño de la muestra, la media de la muestra, ̅𝑋̅̅𝑛̅, cada vez se aproxima más al
valor teórico (𝜇, desconocido) tal que si 𝑛 → ∞ ⇒ ̅𝑋̅̅𝑛̅ → 𝜇 (ley de los grandes números). Esto
también es válido para cualquier momento, p. ej.: (𝑋12 , 𝑋22 , … , 𝑋𝑛2 )
La distribución empírica obtenida de la muestra (se entiende la distribución discreta que se
obtiene de elegir al azar uno de los valores muestrales) también se aproxima hacia la
distribución de la población. Sera una función escalera:
𝐹𝑛∗ (𝑥) =
𝑛º 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜𝑠 𝑚𝑢𝑒𝑠𝑡𝑟𝑎𝑙𝑒𝑠 ≤ 𝑥
,
𝑛
𝑝𝑎𝑟𝑎 𝑐𝑎𝑑𝑎 𝑥 ∈ ℝ
Teorema Glivenko - Cantelli ⇒ La función de distribucion empírica converge uniformemente
hacia la función de distribución de la población con probabilidad uno
Distribuciones que se presentan en le muestreo
Tomamos una muestra aleatoria simple: (𝑋1 , 𝑋2 , … , 𝑋𝑛 ) de una población 𝑋.
Tipos de distribución:
 Distribución Gamma
 Distribución 𝜒 2 (ji-cuadrado)
 Distribución 𝑡 de Student
Distribución Gamma
Estudio de fenómenos con distribución exponencial de parámetro 𝜆 > 0.
El instante 𝑇 en que ocurre la 𝑛-ésima observación del fenómeno:
𝑇 = 𝑋1 + 𝑋2 + ⋯ + 𝑋𝑛
La función de densidad de 𝑇 para 𝑡 > 0 es la función de densidad de gamma:
𝛾(𝑛, 𝜆)(𝑥) = 𝑓𝑛,𝜆 (𝑡) =
𝜆𝑛 𝑛−1 −𝜆𝑡
𝑡
𝑒
Γ(𝑛)
Válida para 𝑛 > 0 (no solo enteros) y Γ(𝑛) es para normalizar y cumple:
Γ(𝑝 + 1) = 𝑝Γ(𝑝)
Γ(𝑝) = (𝑝 − 1)Γ(𝑝 − 1) = (𝑝 − 1)(𝑝 − 2)Γ(𝑝 − 2) = ⋯ = (𝑝 − 1)(𝑝 − 2)(𝑝 − 3) … 1Γ(1)
con Γ(1) = 1. Si 𝑝 es entero ⇒ Γ(𝑝) = (𝑝 − 1)!
∞
Γ(𝑛) = ∫ 𝑡 𝑛−1 𝑒 −𝑡 𝑑𝑡
0
Distribución 𝝌𝟐 de Pearson
Para una población descrita por una variable aleatoria unidimensional 𝑋, con distribución
teórica 𝒩(0,1)
La distribución suma de los cuadrados: ∑𝑛𝑖=1 𝑋𝑖2 es la distribución 𝜒 2 (ji-cuadrado):
𝑓𝑛 (𝑦) =
1
𝑛
𝑦2
𝑛
𝑛
22 Γ ( )
2
−1 −
𝑒
𝑦
2
𝑛 1
Pertenece al modelo de la distribución gamma con 𝑓𝑛 (𝑦) = 𝑔 (2 , 2)
La distribución 𝜒 2 solo depende de un parámetro, 𝑛.
La media y la varianza de 𝜒 2 ⇒ 𝐸{𝑌} = 𝐸{∑𝑛𝑖=1 𝑋𝑖2 } = 𝑛, 𝜎𝑌2 = 2𝑛
2
Si 𝑌1 e 𝑌2 son variables aleatorias independientes con distribuciones 𝜒𝑛2 y 𝜒𝑚
, entonces
𝑚+𝑛 2
2
𝑌 = 𝑌1 + 𝑌2 = ∑𝑖=1 𝑋𝑖 tiene distribución 𝜒𝑛+𝑚
Si (𝑋1 , … , 𝑋𝑛 ) es una muestra aleatoria simple con distribución 𝒩(0, 𝜎), el estadístico
1
𝑌𝑛 = 𝜎2 ∑𝑛𝑖=1 𝑋𝑖2 tiene distribución 𝜒𝑛2 .
En este caso, el estadístico media muestral y la varianza muestral 𝑠 2 :
𝑛
1
𝑋̅ = ∑ 𝑋𝑖
𝑛
𝑛
𝑠2 =
𝑖=1
1
∑(𝑋𝑖 − 𝑋̅)2
𝑛
𝑖=1
𝑋̅ y 𝑠 2 son independientes
Teorema de Fisher ⇒ Si 𝑌 = 𝑛
𝑠2
,
𝜎2
2
su distribucion sera 𝑋𝑛−1
Distribución 𝒕 de Student
Si (𝑋1 , … , 𝑋𝑛 ) es una muestra aleatoria simple de una población 𝒩(𝜇, 𝜎), el estadístico de
Student tiene distribución 𝑡 de Student tiene distribución 𝑡 de Student con 𝑛 − 1 grados de
libertad:
𝑋̅ − 𝜇
𝑌 = √𝑛 − 1
𝑠
−𝑛+1
𝑛+1
1 Γ( 2 )
𝑡2 2
𝑓𝑛 (𝑡) =
(1 + )
𝑛
√𝑛𝜋 Γ (𝑛)
2
Está definida para (−∞, ∞) y es simétrica respecto al origen
UNED
Unidad Didáctica IV:
Inferencia estadística
Cuarto tema de la asignatura de Estadística del Grado en Ingeniería
Informática
26/05/2018
Inferencia estadística
Inferencia estadística ⇒ Proceso de extraer conclusiones generales válidas para toda la
población a partir de una muestra aleatoria tomada por esta.
Punto de partida ⇒ Se conoce parcialmente el modelo estadístico del fenómeno estudiado. Se
pretende mejorar esta información a partir de la información obtenida de las muestras
aleatorias.
Estimaciones por punto
A partir de las observaciones muestrales 𝑋1 , 𝑋2 , … , 𝑋𝑛 , un estimador puntual de un parámetro
es un estadístico 𝑇(𝑋1 , … , 𝑋𝑛 ) (que es función de las muestras (𝑥2 , … , 𝑥𝑛 )).
Si queremos estimar 𝜃 → El valor estimado a partir del muestreo: 𝜃̂ = 𝑇(𝑥1 , … , 𝑥𝑛 ).
La cuestión va a ser elegir el estadístico que adoptaremos como estimador.
Estimadores insesgados
Sesgo y estimador insesgado ⇒ Si 𝑇(𝑋1 , 𝑋2 , … , 𝑋𝑛 ) es un estimador del parámetro 𝜃, la
diferencia
𝑏 = 𝐸{𝑇} − 𝜃
es el sesgo del estimador
Si 𝑏 = 0 → El estimador se denomina centrado o insesgado
Estimadores sesgados e insesgados ⇒ La media muestral, 𝑋̅, es un estimador insesgado de la
media de la población. La cuasivarianza muestral 𝑆 2 es un estimador insesgado de la varianza
de la población. La varianza muestral 𝑠 2 es un estimador sesgado de 𝜎 2 y tiene un sesgo
𝑏=−
𝜎2
𝑛
𝑛
1
𝑋̅ = ∑ 𝑋𝑖
𝑛
𝑖=1
𝑛
𝑆2 =
1
∑(𝑋𝑖 − 𝑋̅)2
𝑛−1
𝑛
𝑠2 =
𝑖=1
1
∑(𝑋𝑖 − 𝑋̅)2
𝑛
𝑖=1
Sesgo (𝑏) y varianza (𝜎 2 )
Generalmente 𝜎 2 , varianza del estimador, disminuya con 𝑛 ⇒ La precisión aumenta con el
tamaño de la muestra, pero si el estimador está sesgado, la mayor parte de las estimaciones
estarán sistemáticamente apartadas del valor a estimar (1ª diana)
La aspiración de la Inferencia estadística no es que cada estimación de en el blanco, si no
desarrollar un método para estimar que, aplicada muchas veces, produzca un alto porcentaje
de estimaciones aceptables
Estadísticos suficientes
Estimador suficiente ⇒ Un estadístico es suficiente para la estimación de un parámetro si la
distribución de la muestra condicionada por el estadístico es independiente del parámetro.
Dada una población con función de distribución 𝐹(𝑥, 𝜃) y una muestra aleatoria simple,
(𝑋1 , … , 𝑋𝑛 ), de esta población, decimos que un estadístico 𝑇(𝑋1 , … , 𝑋𝑛 ) es suficiente para
estimar 𝜃 si la distribución de la muestra, condicionada por el valor del estadístico 𝑇, no
depende de 𝜃.
Criterio general para considerar el estadístico suficiente ⇒ Teorema de factorización
Consideramos una población cuya distribución según la función 𝐹(𝑥, 𝜃), y una muestra
aleatoria simple (𝑋1 , … , 𝑋𝑛 ) representemos por 𝑓(𝑥1 , … , 𝑥𝑛 ) la función de probabilidad (de
densidad si es continua). Condición necesaria y suficiente para que un estadístico 𝑇(𝑋1 , … , 𝑋𝑛 )
sea suficiente es que 𝑓(𝑥1 , … , 𝑥𝑛 ) se puede factorizar como
𝑓(𝑥1 , … , 𝑥𝑛 ) = 𝑔(𝑇(𝑥1 , … , 𝑥𝑛 ), 𝜃)ℎ(𝑥1 , … , 𝑥𝑛 )
siendo 𝑔 una función que solo depende de la muestra a través del valor 𝑇(𝑥1 , … , 𝑥𝑛 ) que toma
el estadístico y ℎ(𝑥1 , … , 𝑥𝑛 ) una función que no depende de 𝜃.
Estimadores de máxima verosimilitud
Tirar 100 veces una moneda y todas den cara, no nos hace pensar que este equilibrada,
aunque la estadística nos permita el capricho.
Principio de máxima verosimilitud ⇒ La aparición de un suceso debe ser atribuida a aquel
modelo, entre los posibles modelos probabilísticos del fenómeno aleatorio, que haga máxima
la probabilidad de que ocurra el suceso.
Estimador de máxima verosimilitud
 Población con distribución de parámetro 𝜃 (desconocido que toma valores en un
espacio paramétrico 𝛩).
 (𝑋1 , … , 𝑋𝑛 ) muestra aleatoria simple de esta población
 𝑓(𝑥1 , … , 𝑥𝑛 ; 𝜃) su función de probabilidad (densidad en continuo).
La función
𝜃 ↦ 𝑓(𝑥1 , … , 𝑥𝑛 ; 𝜃)
función de verosimilitud de la muestra (𝑥1 , … , 𝑥𝑛 ).
Un estimador 𝜃̂ = 𝜃̂(𝑥1 , … , 𝑥𝑛 ) es estimador de máxima verosimilitud de 𝜃 si para cada
(𝑥1 , … , 𝑥𝑛 ) la función de verosimilitud alcanza su máximo cuando 𝜃 = 𝜃̂:
𝑓(𝑥1 , … , 𝑥𝑛 ; 𝜃̂) = max 𝑓(𝑥1 , … , 𝑥𝑛 ; 𝜃)
𝜃∈Θ
Intervalos de confianza
Para un muestreo de un estimador centrado, 𝑇, de parámetro 𝜃, la varianza de 𝑇 tiende a 0
aumentando 𝑛 ⇒ Los valores de 𝑇 se agruparán alrededor de 𝜃.
Si conocemos la distribución en el muestreo del estadístico 𝑇 y su valor observado en una
realización de la muestra podemos diseñar un método para determinar unos márgenes de
variación alrededor de 𝑇 entre los que esperamos que se encuentre el parámetro ⇒
Estimación por intervalos de confianza
Estimación por intervalos de confianza ⇒ Emplea la información obtenida de la muestra para
reducir la incertidumbre sobre la variación de 𝜃.
El intervalo numérico:
(𝑥̅ − 𝑧𝛼
𝜎
√𝑛
, 𝑥̅ + 𝑧𝛼
𝜎
√𝑛
)
se denomina intervalo de confianza para 𝜽 con nivel de confianza 𝜶, 0 < 𝛼 < 1 (confianza del
100𝛼 %)
La amplitud del intervalo es 2𝑧𝛼 𝜎/√𝑛
Método de la cantidad pivotal para la construcción de intervalos de confianza
𝑇(𝑋1 , … , 𝑋𝑛 ; 𝜃) estadístico con distribución independiente de 𝜃. Fijamos 0 < 𝛼 < 1 ⇒ Se
pueden determinar dos constantes tq:
𝑃(𝑐1 ≤ 𝑇(𝑋1 , … , 𝑋𝑛 ; 𝜃) ≤ 𝑐2 ) ≥ 𝛼
Si podemos separar 𝑇 de la parte que depende de 𝜃
𝑐1 ≤ 𝑇(𝑋1 , … , 𝑋𝑛 ; 𝜃) ≤ 𝑐2 ⇒ 𝑡1 (𝑋1 , … , 𝑋𝑛 ; 𝑐1 ) ≤ 𝑔(𝜃) ≤ 𝑡2 (𝑋1 , … , 𝑋𝑛 ; 𝑐2 )
𝑃(𝑡1 (𝑋1 , … , 𝑋𝑛 ; 𝑐1 ) ≤ 𝑔(𝜃) ≤ 𝑡2 (𝑋1 , … , 𝑋𝑛 ; 𝑐2 )) ≥ 𝛼
de donde sacamos un intervalo de confianza con nivel de confianza 𝛼.
Intervalos de confianza para los parámetros de las distribuciones normales
Consideremos una población con distribución 𝒩(𝜇, 𝜎), de la que tomamos una muestra
aleatoria simple (𝑋1 , … , 𝑋𝑛 ). Sea 𝑧𝛼 , un valor que cumple 𝑃(𝑍 > 𝑧𝛼 ) =
𝛼
2
siendo 𝑍 una
variable normal 𝒩(0,1). Entonces el intervalo numérico
(𝑥̅ − 𝑧𝛼
𝜎
√𝑛
, 𝑥̅ + 𝑧𝛼
𝜎
√𝑛
)
es el intervalo de confianza para la media 𝜇 con nivel de confianza 𝛼, donde 0 < 𝛼 < 1 (o
100𝛼 %)
Consideremos una población con distribución 𝒩(𝜇, 𝜎), de la que queremos conocer 𝜇, pero
desconocemos la varianza 𝜎. Tomamos de esta población una muestra aleatoria simple
(𝑋1 , … , 𝑋𝑛 ). Sea 𝑡𝑛−1;𝛼 el valor que cumple 𝑃(𝑡𝑛−1 > 𝑡𝑛−1;𝛼 ) =
𝛼
2
siendo 𝑡𝑛−1 una variable de
Student con 𝑛 − 1 grados de libertad. Entonces el intervalo numérico
(𝑥̅ − 𝑡𝑛−1;𝛼
𝑆
√𝑛
, 𝑥̅ + 𝑡𝑛−1;𝛼
𝑆
√𝑛
)
es el intervalo de confianza para la media 𝜇 con nivel de confianza 𝛼, donde 0 < 𝛼 < 1 (o del
100𝛼 %).
𝑆 es la covarianza muestral (estimador insesgado de la varianza de la población)
𝑛
1
𝑆 =
∑(𝑥𝑖 − 𝑥̅ )2
𝑛−1
2
𝑖=1
Consideremos una población con distribución 𝒩(𝜇, 𝜎), de la que no conocemos ni 𝜇 ni 𝜎.
Queremos calcular 𝜎
El teorema de Fisher asegura que el estadístico
𝑛
𝑛𝑠 2
1
= 2 ∑(𝑋𝑖 − 𝑋̅)2
2
𝜎
𝜎
𝑖=1
tiene una distribución
2
(ji) 𝜒𝑛−1
𝛼
2
Fijado el nivel de confianza 𝛼, en la tabla de 𝜒 2 podemos encontrar dos valores: 𝜒𝑛−1
(1 − 2 )
𝛼
2
y 𝜒𝑛−1
( 2 ) tal que:
𝛼
𝛼
2
𝑃 (𝜒 2 > 𝜒𝑛−1
(1 − )) = 1 −
2
2
𝛼
𝛼
2
𝑃 (𝜒 2 > 𝜒𝑛−1
( )) =
2
2
que verifica:
𝛼
𝑛𝑠 2
𝛼
2
2
𝑃 (𝜒𝑛−1
(1 − ) < 2 < 𝜒𝑛−1
( )) = 𝛼
2
𝜎
2
Despejando 𝑠 2 , obtenemos:
𝑃(
𝑛𝑠 2
𝑛𝑠 2
2
<
𝜎
<
𝛼
𝛼 )=𝛼
2
2
𝜒𝑛−1
(2 )
𝜒𝑛−1
(1 − 2 )
Contraste de hipótesis
Contrastes o test de hipótesis ⇒ Técnicas de inferencia que persiguen descartar ciertas
conjeturas acerca de un modelo probabilístico como consecuencia de la información aportada
por una muestra.
 Hipótesis nula ⇒ La hipótesis previa
 Hipótesis alternativa ⇒ Valores que nos quedan después de descartar la hipótesis
nula
La 𝐻0 sólo será rechazada si hay una fuerte evidencia en su contra; la falta de rechazo de 𝐻0
no es una prueba de hipótesis, sino que es falta de evidencia en su contra.
 Hipótesis simples ⇒ Hipótesis que determinan unívocamente el modelo probabilístico
 Hipótesis compuestas ⇒ Hipótesis que contienen varios posibles distribuciones de
población
Planteamiento general de los contrastes de hipótesis
Región crítica de un test ⇒ Subconjunto de las muestras que llevan a rechazar la hipótesis
nula. Se denota por 𝐶 (𝑐 ∈ 𝐶)
 Si 𝑋 > 𝑐, entonces rechazamos 𝐻0
 Si 𝑋 ≤ 𝑐, entonces no rechazamos 𝐻0
Nos encontramos con cuatro casos:
𝑯𝟎 es cierta
𝑯𝟎 es falsa
Rechazar 𝑯𝟎
Error tipo I
Decisión correcta
No rechazar 𝑯𝟎 Decisión correcta
Error tipo II
Limitar o controlar de alguna manera la frecuencia con que suceden estos dos errores es el
principal objetivo de los contrastes de hipótesis
Las probabilidades de cometer estos errores:
𝑃(Error tipo I) = 𝑃(Rechazar H0|H0 cierta) = 𝑃(𝐶|H0 cierta)
𝑃(Error tipo II) = 𝑃(No rechazar H0|H0 falsa) = 𝑃(𝐶 𝑐 |H0 falsa)
Disminuir 𝐶, aumenta su complementario 𝐶 𝑐 , lo que aumenta la probabilidad de error tipo
II → Disminuir un error, aumenta la posibilidad el otro.
Criterio para el diseño de un test de hipótesis
1) Fijar, en función de las hipótesis y el contexto del problema, una cota para la
probabilidad de cometer el error tipo I. Esta cota es el nivel de significación del
contraste y se representa por 𝛼.
2) Elegir entre los tests cuya probabilidad de error de tipo I es menor que 𝛼, el test que
hace mínima la probabilidad del error de tipo II.
Potencia del test (𝜷) ⇒ Probabilidad de rechazar la hipótesis nula 𝐻0, cuando el valor del
parámetro es 𝜃1 .
𝛽(𝜃1 ) = 𝑃(𝐶|𝜃 = 𝜃1 ) = 1 − 𝑃(Error tipo II)
El test óptimo para contrastar la hipótesis simple 𝐻0: 𝜃 = 𝜃0 frente a la alternativa simple
𝐻1: 𝜃 = 𝜃1 se alcanza eligiendo, entre los tests que tienen un nivel de significación menor o
igual que un valor prefijado, 𝛼, el contraste que tenga máxima potencia 𝛽(𝜃1 ).
Lema de Neyman-Person
Consideremos una población cuya distribución depende de un parámetro 𝜃 desconocido
supongamos que tiene distribución continua con función de densidad 𝑓(𝑥, 𝜃). La función de
densidad de una muestra aleatoria de tamaño 𝑛 sabemos que es igual a:
𝑓(𝑥1 , … , 𝑥𝑛 ; 𝜃) = 𝑓(𝑥1 ; 𝜃) … 𝑓(𝑥𝑛 ; 𝜃)
el test de máxima potencia para contrastar la hipótesis 𝜃 = 𝜃0, frente a 𝜃 = 𝜃1 tiene una
región crítica definida por
𝑓(𝑥1 , … , 𝑥𝑛 ; 𝜃1 )
>𝑐
𝑓(𝑥1 , … , 𝑥𝑛 ; 𝜃0 )
para alguna constante 𝑐.
Contrastes de hipótesis unilaterales y bilaterales
La mayor parte de los problemas corresponden a parámetros unidimensionales con hipótesis
de algunos de los casos siguientes:
Caso 1: 𝐻0: 𝜃 = 𝜃0 frente a 𝐻1: 𝜃 > 𝜃0
Caso 2: 𝐻0: 𝜃 = 𝜃0 frente a 𝐻1: 𝜃 < 𝜃0
Caso 3: 𝐻0: 𝜃 ≤ 𝜃0 frente a 𝐻1: 𝜃 > 𝜃0
Caso 4: 𝐻0: 𝜃 ≥ 𝜃0 frente a 𝐻1: 𝜃 < 𝜃0
Caso 5: 𝐻0: 𝜃 = 𝜃0 frente a 𝐻1: 𝜃 ≠ 𝜃0
Los casos 1-4 son hipótesis unilaterales, y el caso 5 es hipótesis bilateral.
Caso 5 ⇒ Generalmente se elige una región crítica simétrica:
{𝑋̅ > 𝑐} ∪ {𝑋̅ < −𝑐}
Contrastes de bondad del ajuste
Estos contrastes están diseñados para verificar si las proporciones en las que la población, se
reparte en diversas clases o categorías se ajustan a determinado patrón.
Se aplica a los individuos de una población de tal manera que puedan dividirse en un número 𝑘
de grupos: 𝐶1 , … , 𝐶𝑘 sobre los cuales la hipótesis 𝐻0 indica sus frecuencias 𝑝1 , … , 𝑝𝑘 con las
que deberían presentarse. El contraste de 𝐻0 se basa en la obtención de una muestra
aleatoria de tamaño 𝑛, con la cual calcular las frecuencias reales observadas 𝑝
̂,
̂𝑛
1 …,𝑝
 Clases:
 𝐻0
 Muestra
𝐶1
𝑝1
𝑝
̂1
𝐶2
𝑝2
𝑝
̂2
…
…
…
𝐶𝑛
𝑝𝑛
𝑝
̂𝑛
Se basa en un estadístico que mide la discrepancia entre las 𝑝̂𝑖 y las 𝑝𝑖 (observadas y
esperadas)
Discrepancia 𝑫
𝑛
𝑛
𝑖=1
𝑖=1
(𝑝̂𝑖 − 𝑝𝑖 )2
𝑝̂𝑖 2
𝐷 = 𝑛∑
= 𝑛 (1 − ∑ )
𝑝𝑖
𝑝𝑖
Valores pequeños de 𝐷 indican que no hay diferencias importantes. Valores grandes de 𝐷
indica escasa concordancia.
Región crítica del contraste
{𝐷 > 𝑑∗ } ⇒ rechazo de 𝐻0
En las circunstancias descritas, supuesto que el tamaño muestral es grande (𝑛 > 30 y
𝑛𝑝𝑖 > 5 ∀𝑝𝑖 ), si 𝐻0 es cierta, 𝐷 tiene distribución 𝜒 2 con 𝑘 − 1 grados de libertad, siendo 𝑘 el
nº de categorías en las que se ha clasificado la población
UNED
Unidad Didáctica V:
Modelos de optimización
Quinto tema de la asignatura de Estadística del Grado en Ingeniería
Informática
27/05/2018
Sistemas y modelos
Problema de decisión óptima ⇒ Cuando un decisor (individuo, grupo, institución) tiene que
elegir entre diversas alternativas, disponiendo de un criterio para comparar dichas
alternativas.
El objetivo del decisor es encontrar la solución del problema (que resulte mejor según el
criterio)
Ejemplo ⇒ Problema de selección de la cartera
 Decisor ⇒ Individuo (o banco) que tiene dinero y lo quiere invertir
 Alternativas ⇒ Bonos, acciones, inmuebles, pisos, pagares, etc
 Criterio ⇒ Depende del punto de vista:
o de rentabilidad ⇒ Inversión de rentabilidad máxima
o de riesgo ⇒ Inversión de mínimo riesgo
Sistemas
Conjunto de hombres (individuo, grupo, institución,…) y máquinas (ingenio mecánico que hace
cierta tarea, estructura social que responde a unas reglas de conducta) que actúan de modo
interactivo en un determinado ámbito.
Cuando los hombres actúan sobre las máquinas, la respuesta de las máquinas afecta a los
sistemas. Objetivo ⇒ Encontrar la mejor manera de diseñar y operar el sistema.
Modelos
Representación aproximada de un sistema real
Tipos de modelos
 Físicos ⇒ Se puede tocar (maqueta)
 Formales ⇒ Descripción abstracta (oral, dibujos, matemática)
Modelo matemático de optimización
Elementos
 Variables ⇒ Números reales que representan las alternativas del sistema
 Restricciones ⇒ Igualdades o desigualdades que ligan las variables y las relacionan
entre sí (condiciones del sistema)
 Función objeto ⇒ Función que depende de las variables y sirve para comparar las
alternativas
Fases para la creación de un modelo
1)
2)
3)
4)
5)
Análisis del sistema
Formulación del modelo
Solución del modelo
Validación del modelo ⇒ Si no es válido volver al 2
Puesta en práctica de la solución
Características de los modelos de optimización
Características que presentan normalmente las situaciones reales y cuál puede ser su
tratamiento para considerarlas dentro de un modelo de optimización
 Objetivo
o Múltiples objetivos en conflicto entre sí (bueno, bonito y barato, todo es
incompatible)
o Optimización multiobjetivo y difusa ⇒ Construir una única función criterio
mediante la ponderación de los objetivos individuales. La ponderación se
jerarquiza la importancia relativa de cada objetivo parcial
o Optimización por metas ⇒ Fijar unos niveles mínimos aceptables para todos
los objetivos menos uno, y optimizar éste cumpliendo los requisitos mínimos
de los otros objetivos
o Optimización ⇒ Tanto puede ser un proceso de maximización (mayor precio)
como minimización (menor gasto)
 Variables
o Variables ⇒ Representación numérica de las alternativas del modelo. Su
elección es clave. Tipos ⇒ Controlables (precio), incontrolables (número de
ventas, v)
o Constantes ⇒ Cantidades que influyen pero que nadie puede modificar
porque representa una definición o condición natural o física.
o Parámetros ⇒ Cantidades elegidas por el decisor, el cual fija su valor para
cada aplicación concreta del modelo (a)
 Restricciones
o Condiciones que describen el comportamiento del modelo. Ecuaciones e
inecuaciones que relacionan las variables (v), constantes (c) y parámetros (p).
o Tipos
 Restricciones de definición ⇒ Describen igualdades físicas
 Restricciones empíricas ⇒ Describen relaciones causa - efecto entre v,
c, p
 Restricciones normativas ⇒ Describen cuál debe ser el
comportamiento del sistema en el futuro (exigencias del decisor sobre
requisitos mínimos, inversiones máximas, etc) (la relación sacada de
datos históricos no suele ser buena, ya que corresponde al
comportamiento bajo una situación diferente). Es deseable que las
funciones sean continuas, derivables, etc. para una mayor rapidez de
resolución
 Restricciones de acotación ⇒ Acotación de las variables (dentro de un
intervalo)
 Datos
o La incorporación de según qué datos responde a una mayor o menor
complejidad del modelo
o Deben ser cuantitativos, si no los métodos de optimización no son los
adecuados para tratarlos
 Solución
o No todos los problemas tienen solución o, al menos, de manera eficiente (en
tiempo, p.e.)
o Los algoritmos funcionará mejor si las restricciones son funciones suaves
(derivables y continuas), tenemos las variables acotadas, etc.
o Si el algoritmos falla, hay que simplificar el modelo y modificar los requisitos
 Optimización dinámica
o El proyecto de optimización tiene lugar en el tiempo → Objetivos, variables,
restricciones … dependerán del tiempo (los objetivos pueden cambiar a largo
plazo, las variables controlables pueden dejar de serlo, las restricciones
pueden cambiar, los datos pueden dejar de ser representativos, etc).
o Se deben considerar variables y restricciones dependientes del tiempo.
o Optimización dinámica ⇒ Estrategia de resolución temporal, que resuelve en
etapas, donde cada etapa es resuelta mediante técnica de optimización
estática
Formulación de un problema de programación
Planteamiento general
Dadas 𝑛 variables 𝑥1 , … , 𝑥𝑛 , hay que optimizar la función 𝑓(𝑥1 , … , 𝑥𝑛 ) [función objetivo] sujeta
a unas restricciones 𝑔𝑖 (𝑥1 , … , 𝑥𝑛 ) ≥ 0, ℎ𝑗 (𝑥1 , … , 𝑥𝑛 ) = 0
 Optimización ⇒ Maximización o minimización
 Solución factible o realizable ⇒ Cualquier vector (𝑥1 , … , 𝑥𝑛 ) que verifique todas las
restricciones
 Solución óptima ⇒ Solución factible que optimiza la función objetivo
Características y tipos de problemas
 Problema de programación lineal ⇒ Todas las funciones del problema son lineales
(rectas)
 Problema de programación cuadrática ⇒ Función objetivo cuadrática y las demás
lineales
 Problema de programación no lineal ⇒ Si alguna de las funciones del problema es no
lineal
 Problema de programación entera ⇒ Alguna variable sólo toma valores enteros
 Problema de programación estocástica ⇒ En el planteamiento entran consideraciones
de probabilidad
 Problema de programación dinámica ⇒ En la formulación del problema entra el
tiempo
Modelo general de programación lineal
Formal general del problema
Intención ⇒ Simplificar el proceso para poder hacer un programa efectivo general. Dos
posibles formas finales:
 Forma canónica del problema ⇒ Restricciones todas tipo ≤ 𝑏𝑖 con todas las variables
no negativas ≥ 0 y maximización de 𝑓(𝑥1 , … , 𝑥𝑛 ) = 𝑧 función objetivo
 Forma standard ⇒ Restricciones todas de igualdad = 𝑏𝑖 con todas las variables no
negativas ≥ 0 y maximización de 𝑓(𝑥1 , … , 𝑥𝑛 ) = 𝑧 función objetivo
Formulaciones equivalentes
Solución teórica del problema
Consideramos el problema standard con vectores y matrices reales:
𝑀𝑎𝑥 𝑧 = 𝑐 𝑡 𝑥
𝐴𝑥 = 𝑏
𝑥≥0
 Programa o solución realizable o factible ⇒ Conjunto de 𝑥 que satisfacen todas las
restricciones (incluidas las de no negatividad)
 Región factible ⇒ Conjunto de soluciones factibles del problema
 Matriz básica o base del sistema lineal (𝑩) ⇒ Matriz cuadrada de dimensión 𝑚 y
rango 𝑚 sacada de las columnas de 𝐴
 Matriz no básica 𝑵 ⇒ Matriz residual de 𝑛 − 𝑚 columnas cuando sacamos 𝐵 de 𝐴
 Variables básicas (respecto 𝑩) 𝒙𝑩 ⇒ 𝑚 variables asociadas a las columnas de la matriz
𝐵
 Variables no básicas (respecto 𝑩) 𝒙𝑵 ⇒ 𝑛 − 𝑚 variables restantes
 Solución básica ⇒ Vector que es solución de 𝐵𝑥 𝐵 = 𝑏
 Programa básico asociado a 𝑩 ⇒ Solución básica tal que ≥ 0 (verifica todas las
restricciones incluida la de no negatividad)
 Vértice ⇒ Cada uno de los puntos de la región factible cuyas coordenadas se
corresponden con los valores de un programa básico
 Arista o cara ⇒ Cada segmento de recta de restricción comprendido entre dos vértices
 Frontera ⇒ Conjunto de soluciones factibles sobre una arista
 Interior ⇒ Conjunto de soluciones que no están en la frontera
 Programa básico óptimo ⇒ Programa básico que maximiza la función objetivo
(sustituyendo un programa básico, solución básica ≥ 0, el valor de la función objetivo
𝑧 es máxima)
 Programa óptimo ⇒ Programa (básico o no) donde la función objetivo alcanza el valor
máximo (igual al básico óptimo)
 Región óptima ⇒ Conjunto de programas óptimos
 Valor óptimo ⇒ Valor que toma la función objetivo en un programa óptimo
Teorema fundamental de la programación lineal
Dado un problema en forma standard:
 Si existe al menos un programa ⇒ Existe al menos un programa básico
 Si existe al menos un programa óptimo ⇒ Existe al menos un programa básico óptimo
Entonces para resolver un programa basta encontrar los vértices de la región factible
(programas básicos) y comprobar cuál de ellos maximiza la función objetivo (el que lo haga
será un programa básico óptimo)
Situaciones especiales en los problemas de programación lineal
 Múltiples óptimos ⇒ Tendremos infinitas soluciones óptimas (las que están sobre la
arista óptima)
 Región factible no acotada ⇒ Tipos de soluciones
o Valor óptimo infinito ⇒ El problema es no acotado con valor óptimo infinito
o Valor óptimo finito ⇒ Toma un valor óptimo finito
 Región factible vacía ⇒ Ningún punto satisface todas las restricciones. El problema
será no factible y no tiene solución óptima (independientemente de la función
objetivo)