CORRELACION

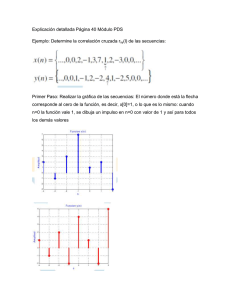
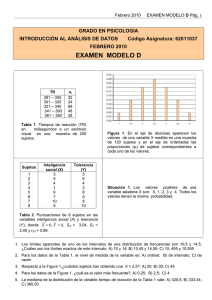
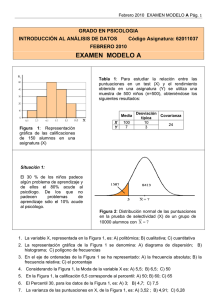
COEFICIENTE DE CORRELACIÓN
LINEAL DE PEARSON
1
DEFINICIÓN
• rXY
• Índice que mide la covariación entre variables: en qué
medida la variación en una variable influye en la
variación en otra variable.
• Variables cuantitavas (escala mínima de intervalo).
• Relación EXCLUSIVAMENTE lineal.
• Valores: -1 ≤ rXY ≤ +1.
• Interprentación:
+1: relación perfecta positiva (directa).
-1: relación perfecta negativa (inversa).
0: ausencia de relación.
2
12
10
8
6
4
2
0
0
1
2
3
4
5
6
Correlación perfecta positiva: rxy = +1 (no común en psicología)
3
20
18
16
14
12
10
8
6
4
2
0
0
2
4
6
8
10
12
Correlación positiva: 0 < rxy < +1
4
25
20
15
10
5
0
0
1
2
3
4
5
6
Correlación perfecta negativa: rxy = -1 (no común en psicología)
5
20
18
16
14
12
10
8
6
4
2
0
0
2
4
6
8
10
12
Correlación negativa: -1 < rxy < 0
6
20
18
16
14
12
10
8
6
4
2
0
0
1
2
3
4
5
6
Ausencia de correlación
7
Fórmulas
 XY
rXY 
rXY 
rXY
 XY
N
S X SY
Puntuaciones directas
 xy
x y
2
Z


X
N
ZY
2
Puntuaciones diferenciales
Puntuaciones estandarizadas
8
Ejemplo
X: 2 4 6 8 10 12 14 16 18 20
Y:1 6 8 10 12 10 12 13 10 22
1. Cálculo de rxy con puntuaciones directas.
2. Cálculo de rxy con puntuaciones diferenciales.
3. Cálculo de rxy con puntuaciones tipificadas.
9
Ejemplo: diagrama de dispersión
¿Qué valor de rxy se espera?
25
20
15
10
5
0
0
5
10
15
20
25
10
Ejemplo: Cálculo de rxy con
puntuaciones directas
X
2
4
6
8
10
12
14
16
18
20
110
Y
1
6
8
10
12
10
12
13
10
22
104
XY
2
24
48
80
120
120
168
208
180
440
1390
X2
4
16
36
64
100
144
196
256
324
400
1540
Y2
1
36
64
100
144
100
144
169
100
484
1342
11
Ejemplo: Cálculo de rxy con
puntuaciones directas
X
X
N
110

 11
10
Sx 
Y 104

Y

 10,4
N
rXY 
10
 XY  X Y
N
S X SY
Sy 
2
X

N
2
Y

N
1540
X 
 112  5,745
10
2
1342
Y 
 10,42  5,103
10
2
1390
 11*10,4
 10
 0,839
5,745 * 5,103
12
Significación
• ¿El valor obtenido como coeficiente de correlación
muestra que las variables X e Y están relacionadas en
realidad, o presentan dicha relación debido al azar?
• Hipótesis nula  H0: rxy = 0. El coeficiente de
correlación obtenido procede de una población cuya
correlación es cero (ρXY = 0).
• Hipótesis alternativa  H1: rXY  0 . El coeficiente de
correlación obtenido procede de una población cuyo
coeficiente de correlación es distinto de cero (ρXY  0 ).
13
Significación
• Fórmula:
t
rXY
1 r
N 2
2
XY
• Interpretación:
– t  t( , N 2)  Se rechaza la Hipótesis nula. La
correlación no procede de una población cuyo
valor ρxy = 0. Las variables están relacionadas.
– t t
 Se acepta la Hipótesis nula. La
( , N  2 )
correlación procede de una población cuyo valor
ρxy = 0. Las variables no están relacionadas.
14
t
rXY
1 r
N 2
2
XY

0,839
1  0,839
10  2
2
 4,37
t( , N 2)  t(0.05,8)  2,306
4,37  2,306
15
Significación: ejemplo
t
rXY
1 r
N 2
2
XY

0,839
1  0,839
10  2
2
 4,37
t( , N 2)  t(0.05,8)  2,306
4,37  2,306
Conclusiones: rechazamos la hipótesis nula con un riesgo
(máximo) de equivocarnos de 0,05. La correlación no procede de
una población caracterizada por una correlación de cero. Ambas
variables están relacionadas.
16
Otras cuestiones a considerar
• Correlación no implica causalidad.
• La significación estadística depende del tamaño de la
muestra (a mayor N, más probable es encontrar
significación).
• Otra posible interpretación la da el coeficiente de
2
determinación rXY
, en términos de proporción de
variabilidad de Y compartida o explicada por X.
• La proporción de variabilidad no explicada, aquello
de Y que queda sin explicar por X, se denomina
2
coeficiente de no determinación: 1  rXY
17
Coeficiente de determinación:
ejemplo
2
rXY
 0,8392  0,704 . El 70,4% de la variabilidad
de Y es explicada por X.
1  rXY2  1  0,8392  0,296 . El 29,6% de la
variabilidad de Y queda sin explicar.
18