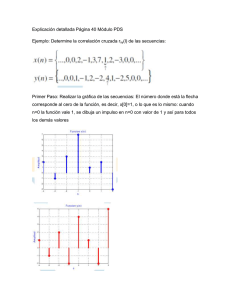
Tema 5. Correlación Lineal

Análisis de Datos I
Esquema del Tema 5
Tema 5. Correlación Lineal
1. RELACIÓN LINEAL
2. CUANTIFICACIÓN DE LA RELACIÓN LINEAL
La Covarianza
La Correlación de Pearson
Matriz de Varianzas-Covarianzas, S
Matriz de Correlaciones, R
3. EJERCICIOS
__________________
Bibliografía: Tema 5 (pág. 139-164)
Ejercicios recomendados: 1, 2, 4, 5, 6, 7, 8, 9,
10, 11 y 12.
Carmen Ximénez
1
Análisis de Datos I
Esquema del Tema 5
1. LA RELACIÓN LINEAL
TIPOS DE RELACIÓN LINEAL
8
7
Ejemplo a) Inteligencia (X) y Rendimiento (Y)
3
6
1
3
2
5
3
7
1
4
Relación directa
o positiva
Y
X:
Y:
6
5
4
3
2
,5
1,0
1,5
2,0
2,5
3,0
3,5
X
6
5
Ejemplo b) Ansiedad (S) y Aciertos (T)
2
4
4
2
6
1
2
3
1
5
Relación inversa
o negativa
T
S:
T:
4
3
2
1
0
0
1
2
3
4
5
6
7
S
9
Ejemplo c) Extroversión (U) y Absentismo (W)
2
5
4
4
4
7
2
4
2
8
Relación lineal
Nula
7
W
U:
W:
8
6
5
4
3
0
1
2
3
4
5
6
U
REPRESENTACIÓN GRÁFICA
Ejemplo 1: Diagrama de Dispersión
SUJ.
1
2
3
4
5
6
7
8
9
10
16
14
12
10
Y 8
6
4
2
0
X
4
4
5
5
7
9
9
9
10
10
Y
6
7
8
10
12
10
13
15
13
15
Se dispone de N pares de puntuaciones (en el ejemplo
para 10 sujetos) en dos variables cuantitativas.
Importante: Tienen que referirse a los mismos sujetos.
X  7,2
Y  10,9
X
a)
b)
Y
c)
d)
0 1 2 3 4 5 6 7 8 9 10
X
Carmen Ximénez
2
Análisis de Datos I
Esquema del Tema 5
2. CUANTIFICACIÓN DE LA RELACIÓN LINEAL
La Covarianza
Sxy 
 X Y -  X Y 
i
i
- Sxy +
N
Sxy 
Otras fórmulas:
x  y
i
i
N
Sxy  rxy  Sx  S y
;
La Correlación de Pearson
rxy 
 N  X Y   X  Y 

N  X   X    N  Y   Y 

i



i
i
2
2
i
Otras fórmulas:
i
2
i
rxy 
i
z
x
 zy
N
2
i
rxy 
;
-1 rxy 1



Sxy
Sx  Sy
En transformaciones lineales la covarianza se altera pero la correlación de Pearson no:
Si: U = a · X + b ; V = c · Y + d
 Suv = (a) (c) Sxy
ruv = rxy (Si a y c tienen signo opuesto: ruv = -rxy )
Matriz de Varianzas-Covarianzas, S
X
S  Y

W
X
S x2
Medias: X
Y
S xy
S y2




W
S xw
S yw

S w2
Y

W
Matriz de Correlaciones, R
X
1
X
R  Y

W
Para pasar de S a R puede aplicarse la fórmula
rxy 
Y
rxy
1






W
rxw
ryw

1
Sxy
Sx  Sy
En los ejemplos anteriores:
Ejemplo a)
Totales:
Medias:
Xi
3
1
2
3
1
10
2
Carmen Ximénez
Yi
6
3
5
7
4
25
5
Xi·Yi
18
3
10
21
4
56
11,2
Xi 2
9
1
4
9
1
24
Yi 2
36
9
25
49
16
135
S xy 
rxy 

X
N
i
 Yi
- X Y
N   Xi  Yi
 11,2-10  1,2



2
 N   Xi    Xi  


5(56)  (10)(25)

2
5(24)  (10)2

  X  Y 
N  Y   Y 
5(135)  (25)2
i
i
2
i

i
 0,95
3
2



=
Análisis de Datos I
Esquema del Tema 5
Si
2
4
6
2
1
15
3
Ti
4
2
1
3
5
15
3
Si·Ti
8
8
6
6
5
33
6,6
Si2
4
16
36
4
1
61
Ui
2
4
4
2
2
Totales: 14
Medias: 2,8
Wi
5
4
7
4
8
28
5,6
Ui·Wi
10
16
28
8
16
78
15,6
Ui2
4
16
16
4
4
44
Ejemplo b)
Totales:
Medias:
Ejemplo c)
Ti 2
16
4
1
9
25
55
Wi2
25
16
49
16
64
170
Matriz de Varianzas-Covarianzas, S
X
Y
X
Y
0 ,80 1, 20
2
S S
T
U
W
Medias:
2
5
Sst 
i
 6,6-9  2,4
i
N
N   Si  Ti
rst 

 S T -S T 

i

 
2
 N   Si    Si   

 
5(33)  (15)(15)
2

5(61)  (15)2

  S  T 
N  T   T 
i
2
i
5(55)  (15)2
i
U W - U W 
ruw 
 U  W 
 
N  U   U    N  W   W 
 

i



N


i
2
i
i
5(78)  (14)(28)
5(44)  (14)2
i
2
2
i

5(170)  (28)2

i
2



 0,05
Matriz de Correlaciones, R
T
0
0 , 20
U
 0, 40
 0,80
W
 0,60
 0,60
X
Y
3, 20
 2 , 40
2
1,60
 1, 20
0,96
0
0,60
 0 ,08
2,64
R S
T
U
W
3
3
2,8
X
1,00
Y
0,95
1,00

 15,6-15,68  0,08
i
N  Ui Wi



 0,95

Suw 
S
 0 , 20
 0 ,60
S
 0,12
 0, 24
T
0,00
0,10
U
 0, 46
 0,58
W
 0, 41
 0, 26
1,00
 0,95
1,00
0,91
 0,87
1,00
0,00
0 , 26
 0,05
1,00
5,6
INTERPRETACIÓN DE rxy
1º. Examinar su magnitud absoluta
rxy 0 … Relación lineal nula
rxy 1 … Relación lineal
2º. Examinar su signo
rxy 0 …. Relación lineal directa
rxy 0 …. Relación lineal inversa
Propiedades de rxy:
2
1. r xy x 100 … % de variabilidad común entre X e Y
Ejemplo: rxy = 0,70 … r2xy = 0,49. Existe un 49% de variabilidad común entre X e Y.
2. rxy = 0 no implica que no haya relación entre X e Y (puede ser de otro tipo)
3. Factores que afectan a rxy: 1) Variabilidad de X, Y y XY, 2) Terceras variables
(efectos moderadores), 3) Que X e Y estén bien medidas (fiabilidad) y 4) La muestra
en que se evalúen X e Y.
4. Para decidir si X e Y están linealmente relacionadas, se realiza una prueba de
significación estadística (contraste de hipótesis sobre xy)
5. La correlación NUNCA IMPLICA CAUSALIDAD, sólo grado de relación lineal.
Carmen Ximénez
2
4

Análisis de Datos I
Esquema del Tema 5
EJEMPLO 2 (resuelto):
X:
Y:
2
3
3
3
5
5
1
2
4
2
a) Calcule la covarianza, la correlación de Pearson y el diagrama de dispersión para las
variables X e Y
b) Calcule la correlación de Pearson y la covarianza para las variables T y W, siendo:
T = 2 · X + 3;
W = 3·Y
Solución:
a)
X:
Y:
X·Y:
X2 :
Y2 :
2
3
6
4
9
3
3
9
9
9
5
5
25
25
25
1
2
2
1
4
4
2
8
16
4
15
15
50
55
51
X
6
Sxy 
5
 Yi
3
2
rxy 
1
0
0
1
2
3
4
5
6

X
b) rtw = rxy = 0,645

- X Y
N
4
Y
i


  X  Y 
  X    N  Y   Y 
N   X i  Yi

2
 N   Xi 


50
 (3)(3)  1
5

i
i
2
2
i
i
i
(5)(50 )  (15 )(15 )
(5)(55 )  (15 ) 2

(5)(51)  (15 ) 2
2



  0,645
Stw = (2) (3) Sxy = (6) (1) = 6
(Pues T y W son transformaciones lineales de X e Y)
EJERCICIOS
1. Obtenga la covarianza y la correlación de Pearson para los datos del ejemplo 1:
SUJ.
1
2
3
4
5
6
7
8
9
10
Totales:
Medias:
X
4
4
5
5
7
9
9
9
10
10
72
7,2
Y
6
7
8
10
12
10
13
15
13
15
109
10,9
Carmen Ximénez
S xy 
rxy 
X
N
i
 Yi

- X Y

 N   X  Y     X  Y 

N   X    X    N  Y   Y 

i



2
i
i
i
i
2
i
2
i
i
2



5

Análisis de Datos I
Esquema del Tema 5
2. Obtenga el diagrama de dispersión, la covarianza y la correlación de Pearson para X
e Y en los siguientes ejemplos:
(a)
Xi
4
3
3
2
5
6
Yi
15
12
10
9
14
13
(b)
Xi
7
10
11
9
8
3
(c)
Yi
6
10
11
11
8
12
Xi
10
8
10
6
7
Yi
4
7
5
7
6
3. A partir de la siguiente matriz de varianzas-covarianzas, realice el volcado a la
matriz de correlaciones:
S=
V
X
Y
4.
CI
CI
RE
R  RA
V
X
Y
12
10
15
14
9
20
RE
0,82
RA
0,61
ML
0,42
DE
0,23
LC
 0,32
0,40
0,15
0,76
0,03
- 0,06
 0,08
- 0,23
 0,15
- 0,41
0,23
ML
DE
LC
(1)
(2)
(3)
(4)
(5)
(6)
CI: Cociente de inteligencia
RE: Razonamiento espacial
RA: Rendimiento académico
ML: Motivación de logro
DE: Debilidad emocional
LC: Locus de control externo
CI: Cociente de inteligencia
¿Qué variable correlaciona más con RA?
¿Qué variable correlaciona menos con ML?
¿Cuál es la mayor correlación encontrada?
¿Cuál es la menor correlación encontrada?
¿RA se relaciona más con CI o con ML?
¿Qué significa la correlación negativa entre ML y LC?
5. Tras medir las variables X (Estrés laboral) e Y (Intención de abandono del puesto de
trabajo) en una muestra, se obtienen los siguientes estadísticos:
S=
X
Y
Medias:
X
33,65
Y
54,8
101,76
11,5
48,8
1. ¿Existe relación entre X e Y? Interprétela.
2. Si se obtienen las variables: U = 2·X + 3 y
V = -3·Y
Obtenga la media y varianza de U y V y la covarianza y correlación entre U y V
Carmen Ximénez
6