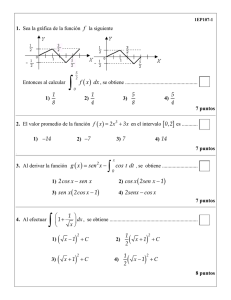
Reglas de derivación:

Reglas de derivación_____________________________________________________________________________________
REGLAS DE DERIVACIÓN
Derivadas inmediatas
f ′(x)
0
p ⋅ x p −1
f (x)
λ
xp
arcsen(x)
a x ⋅ ln a
ex
1
log a e
x
1
x
1
− 2
x
cos(x)
− sen(x)
1
cos 2 ( x)
1
arccos(x)
1 − x2
1
ax
ex
log a x
ln x
1
x
sen(x)
cos(x)
tan(x)
arctan(x)
senh(x)
(seno hiperbólico de x)
cosh(x)
arg senh( x)
(argumento del seno
hiperbólico de x)
arg cosh( x)
(argumento del coseno
hiperbólico de x)
−
1 − x2
1
1+ x2
cosh(x)
(coseno hiperbólico de x)
senh(x)
1
1+ x2
1
x 2 −1
−1
x 2 −1
si x > 1
si x < −1
1
Reglas de derivación_____________________________________________________________________________________
Reglas de derivación
Sean u = f (x) y v = g (x) dos funciones derivables. Se cumple que:
′
Regla de la cadena: ( f  g ) ( x) = ( f ( g ( x )))' = f ′( g ( x) ) ⋅ g ′( x)
Regla de la suma, producto y cociente:
(λ ⋅ u )′ = λ ⋅ u ′ para cualquier
(u ± v )′ = u ′ ± v ′
(u ⋅ v )′ = u ′ ⋅ v ± u ⋅ v ′
λ ∈ℜ
′
 u  u ′v − uv ′
  =
v2
v
Aplicando la regla de la cadena se deduce que:
(u )′ = p ⋅ u
p −1
p
⋅ u′
[ln(u )]′ = u ′
u
[a ] = u ′ ⋅ a
[e ]′ = u ′ ⋅ e
u
u
′
u
⋅ ln a
u
′
u′
1
 u  = − u 2
(sen (u ))′ = u ′ ⋅ cos(u )
(cos (u ))′ = −u ′ ⋅ sen(u )
′
(tan (u ))′ = u2
cos (u )
′
(arcsen (u ))′ = u 2
1− u
′
(arccos (u ))′ = − u 2
1− u
′
(arctan (u ))′ = u 2
1+ u
2
Reglas de derivación_____________________________________________________________________________________
Apéndice: Algunas funciones hiperbólicas
e x − e−x
2
arg senh( x) = ln x + 1 + x 2
senh( x) =
e x + e−x
2
arg cosh( x) = ln x + x 2 − 1
cosh ( x ) =
3