Nombre
Anuncio

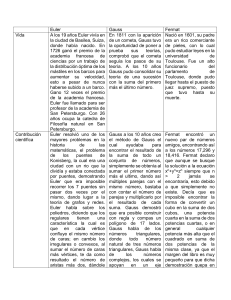
Matemáticas de la Especialidad – Mecánica Grupo: Mecánica 2a Nombre .......................................................................................... Núm. Mat. ............................. Examen de prácticas Ejercicio 1 Tiempo: 1h 30 min. (5 puntos) La concentración de bacterias contaminantes c en un lago decrece de acuerdo con la relación: c = 70 e −1.5 t + 25 e −0.075 t Determina el tiempo requerido para que la concentración de bacterias se reduzca a 9 usando el método de Newton. Utiliza la representación gráfica para obtener la estimación inicial. Estimación inicial: Valor aproximado: El error cometido es inferior a Ejercicio 2 (5 puntos) Consideremos el siguiente problema de valor inicial: x′′ ( t ) + x ( t ) = 6cos ( t ) con x ( 0 ) = 2 y x′ ( 0 ) = 3 1. Utilizando el método de Euler calcule una solución aproximada en el intervalo [0, 2] con: a. b. 2. h = 0.1 h = 0.05 Sabiendo que la solución exacta es: x ( t ) = 2 cos ( t ) + 3sen ( t ) + 3 t sen ( t ) Represente gráficamente, en una misma ventana, la solución exacta y las soluciones aproximadas. En la ventana del gráfico debe aparecer un título que indique lo que representa, así como, tu nombre y tu número de matrícula. 3. Completa la siguiente tabla, redondeando los valores obtenidos a cuatro cifras decimales: t x(t ) Valor aproximado Valor aproximado Método de Euler Método deEuler h = 0.1 0 1 2 h = 0.05