Unidad III Variables Aleatorias Unidimensionales 3.1. EL

Unidad III Variables Aleatorias Unidimensionales
3.1. EL CONCEPTO DE VARIABLE ALEATORIA
En el capítulo anterior se examinaron los conceptos básicos de probabilidad con respecto a eventos
que se encuentran en un espacio muestral. Los experimentos conciben de modo que los resultados
del espacio muestral son cualitativos o cuantitativos. Ejemplos de resultados cualitativos: a) el
lanzamiento de una moneda arroja “cara” o “sello”, b) un producto manufacturado puede ser
“defectuoso” o “no defectuoso”, c) una persona puede preferir el perfume A o B. Puede ser útil la
cuantificación de los resultados cualitativos de un espacio muestral y, mediante el empleo de
medidas numéricas, estudiar su comportamiento aleatorio. El concepto de variable aleatoria
proporciona un medio para relacionar cualquier resultado con una medida cuantitativa.
Una variable aleatoria es una función de valor real cuyo dominio es un
espacio muestral.
Ejemplo 1: Supongamos el lanzamiento de una moneda, los estados posibles son “cara” o
“sello”; su espacio muestral Ω = {“cara” , “sello”}. Sea X(sello) = 0, y X(cara) = 1, de esta
manera transformamos los dos resultados posibles del espacio muestral en puntos sobre la recta de
los reales. Por P(X = 0) se entenderá la probabilidad de que la variable aleatoria X tome el valor 0;
de manera equivalente, la probabilidad de que caiga sello cuando se lance la moneda.
Ejemplo 2: Consideremos el lanzamiento de dos dados equilibrados, el espacio muestral contiene
36 resultado posibles, tal como se muestra en la tabla. Sea la variable aleatoria X la suma de los
valores de los dos dados. La tabla siguiente muestra el espacio muestral, el valor de la variable
aleatoria y su probabilidad:
Espacio muestral
(1, 1)
(1, 2), (2, 1)
(1, 3), (2, 2), (3, 1)
(1, 4), (2, 3), (3, 2), (4, 1)
(1, 5), (2, 4), (3, 3), (4, 2), (5, 1)
(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)
(3, 6), (4, 5), (5, 4), (6, 3)
(4, 6), (5, 5), (6, 4)
(5, 6), (6, 5)
(6, 6)
Variable aleatoria X
2
3
4
5
6
7
8
9
10
11
12
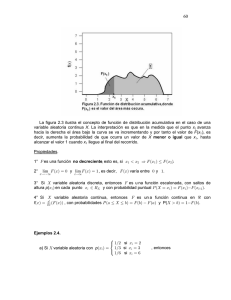
La naturaleza probabilística de la variable aleatoria X,
suma de caras de dos dados, puede observarse al graficar
cada valor de X con su respectiva probabilidad
Frecuencia
1
2
3
4
5
6
5
4
3
2
1
Distribución de Probabilidades para X (suma de
caras de dos dados)
1/6
0,18
0,16
5/36
5/36
0,14
Probabilidad
Las variables aleatorias se representan mediante
mayúsculas, ejemplos X, Y y Z. Los valores numéricos
reales que puede asumir una variable aleatoria se
representarán mediante minúsculas, ejemplos, x, y y z. Se
puede decir “la probabilidad de que X tome el valor x”, y
se denota como P(X = x) o p(x).
Probabilidad
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
1/9
0,12
0,10
1/9
1/12
0,08
1/12
1/18
1/18
0,06
0,04
1/36
1/36
0,02
0,00
2
3
4
5
6
7
8
9
10
11
12
x
En el ejemplo del lanzamiento de la moneda, la variable
aleatoria X sólo tiene 2 valores posibles; es sencillo determinar las probabilidades de esos valores
(P(X = 1) = ½. A una variable aleatoria con esas características se le llama discreta.
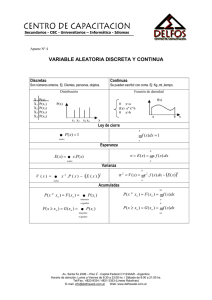
Se dice que una variable aleatoria X es discreta si puede tomar sólo un número finito,
o infinito numerable, de valores posibles x.
En este caso,
¾ P(X = x) = p(x) ≥ 0.
¾ ∑ x P(X = x) = 1, siendo la sumatoria con respecto a todos los valores
posibles de x
A la función p(x) se le llama función de probabilidad de X.
3.2.
Distribución de Probabilidad de variables aleatorias discretas.
La función de distribución acumulativa de la variable aleatoria X es la probabilidad
de que X sea menor o igual a un valor específico de x, y está dada por:
F(x) = P(X ≤ x) = ∑ p(xi) ≥ 0
x i≤ x
El termino más general Distribución de Probabilidad, se refiere a la colección de valores de la
variable aleatoria, a la función de probabilidad, y también a la existencia de la función de
distribución acumulada de X, F(x).
Por lo tanto, en el caso discreto, una variable aleatoria X está caracterizada por la función de
probabilidad p(x), la cual determina la probabilidad puntual de que X = x, y por la función
distribución acumulativa F(x), la que representa la suma de las probabilidades puntuales hasta el
valor x de X inclusive.
Ejemplo 3: Consideremos de nuevo el lanzamiento de dos dados. Si X es la variable aleatoria que
representa la suma de las dos caras, la función de probabilidad de X es
p(x) =
6 - |7 – x|
36
0
x = 2, 3, ....., 12
para cualquier otro valor.
Esta función permite determinar las probabilidades para los valores de X, que se resumen en la
tabla del ejemplo 2. Además, puede evaluarse la función de distribución acumulativa de X de la
siguiente forma:
F( 1) = P(X ≤ 1) = 0
F( 2) = P(X ≤ 2) = 1/36
F( 3) = P(X ≤ 3) = 3/36
F( 4) = P(X ≤ 4) = 6/36
...............
F(11) = P(X ≤ 11) = 35/36
F(12) = P(X ≤ 12) = 1
Además,
P(X > 7) = 1 – P(X ≤ 7) = 1 – F(7) = 15/36
P( 5 ≤ X ≤ 9) = P(X ≤ 9) – P(X ≤ 4) = F(9) – F(4) = 24/36
En general, la función de distribución acumulativa F(X) de una variable aleatoria discreta es una
función no decreciente de los valores de X, de tal manera que:
1. 0 ≤ F(x) ≤ 1,
para cualquier x
2. F( xi ) ≥ F( xj ), si xi ≥ xj
3. P(X > x) = 1 – F(x)
Además puede establecerse que para variables aleatorias de valor entero se tiene:
4. P(X = x) = F(x) – F(x – 1)
5. P(xi ≤ X ≤ xj ) = F( xi ) – F( xi – 1)
3.3.
Distribución de Probabilidad de variables aleatorias continuas.
En el caso discreto, se asignan probabilidades positivas a todos los valores puntuales de la variable
aleatoria, pero la suma de todas ellas es uno aún a pesar de que el conjunto sea infinito numerable;
para el caso continuo, lo anterior no es posible, la probabilidad de que una variable aleatoria
continua X tome un valor específico x es cero.
La distribución de probabilidad de una variable aleatoria continua X está caracterizada por una
función f(x) que recibe el nombre de función de densidad de probabilidad. Como la probabilidad de
que X tome un valor específico es cero, la función permite determinar la probabilidad de un
intervalo a ≤ X ≤ b.
Se dice que una variable aleatoria X es continua si puede tomar un número infinito de
valores posibles asociados con intervalos de números reales, y hay una función f(x),
llamada la función de densidad de probabilidad, tal que:
¾ f(x) ≥ 0, para todo x
∞
¾ ∫ f(x) dx = 1
-∞
b
¾ P(a ≤ X ≤ b) = ∫ f(x) dx
a
f(x)
a
b
x
La probabilidad P(a ≤ X ≤ b) representa el área bajo f(x) en el intervalo [a, b], y el área total bajo
f(x) es uno.
Al igual que en el caso discreto, la función de distribución acumulativa de una variable aleatoria
continua X es la probabilidad de que X tome un valor menor o igual a algún a específico. Esto es,
a
P( X ≤ a) = F(a) = ∫ f(x) dx
-∝
f(x)
a
x
Dado que para cualquier variable aleatoria continua X, P(X = x) = 0, entonces
P(X ≤ x) = P( X < x ) = F(x)
Ejemplo 4: la variable aleatoria X representa el intervalo de tiempo entre dos llegadas
consecutivas a una tienda y su función de densidad de probabilidad está dada por:
k e– x/2
x>0
f(x) =
0
para cualquier otro valor
Determine k, ¿Cuál es la probabilidad de que el tiempo esté entre 2 y 6 minutos?. ¿Cuál es la
probabilidad de que transcurran menos de 8 minutos?, ¿Cuál es la probabilidad de que transcurran
mas de 8 minutos?.
Ejemplo 5: la variable aleatoria que representa la proporción de accidentes automovilísticos
fatales tiene la siguiente función de densidad:
42x(1 – x)5
f(x) =
0
0≤ x ≤ 1
para cualquier otro valor
¿Cuál es la probabilidad de que no más del 25% de los accidentes automovilísticos sean fatales?.
En otras palabras, ¿cuál es P(X ≤ 0.25) ?
3.4.
Valor esperado de una variable aleatoria.
La probabilidad la podemos interpretar como la frecuencia relativa a largo plazo de que suceda un
evento, la distribución de probabilidades entonces es la frecuencia relativa a largo plazo de los
resultados numéricos asociados con un experimento. En relación con lo anterior, podemos
considerar el valor promedio de una variable aleatoria después de un número grande de
experimentos como su valor esperado.
El valor esperado ( o esperanza) de una variable aleatoria es un concepto muy importante en el
estudio de las distribuciones de probabilidades. Este término tiene sus orígenes en los juegos de
azar, debido a que los apostadores deseaban saber cuál era su esperanza de ganar repetidamente un
juego, en este sentido, el valor esperado representa la cantidad de dinero promedio que el jugador
está dispuesto a ganar o perder después de un número grande de apuestas.
Ejemplo 6: supóngase que se tiene una moneda normal y el jugador tiene tres oportunidades para
que al lanzarla aparezca una “cara”. El juego termina en el momento en el que cae una “cara” o
después de tres intentos, lo que suceda primero. Si en el primero, segundo o tercer lanzamiento
aparece “cara” el jugador recibe $2, $4, y $8 respectivamente. Si no cae “cara” en ninguno de los
tres lanzamientos, pierde $20.
Sea X la variable aleatoria que representa la cantidad que se gana o se pierde cada vez que se juega.
Después de un número grande de juegos se espera ganar $2 en uno de dos juegos, $4 en
cualesquiera de cuatro juegos, $8 en uno de cada 8 juegos, y se espera perder $20 una vez cada 8
juegos. El valor esperado, o la cantidad promedio que se ganaría en cada juego después de un
numero grande de intentos, se determina multiplicando cada cantidad que se gana/pierde por su
respectiva probabilidad y sumando los resultados. De acuerdo con esto, la esperanza de ganar es
$2 * (1/2) + $4 * (1/4) + $8 * (1/8) + (-$20)*(1/8) = $0.50 por juego.
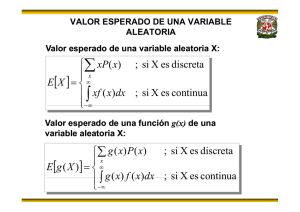
El valor esperado de una variable aleatoria X es el promedio o valor medio de X,
está dado por:
¾ E [X] = ∑ x p(x)
y
si x es discreta
∞
si x es continua
¾ E[X] = ∫ x f(x) dx
-∞
en donde p(x) y f(x) son las funciones de probabilidad y de densidad de
probabilidad, respectivamente.
Ejemplo 7: sea la variable aleatoria X, definida en el ejemplo 2 (la suma en el lanzamiento de dos
dados), compruebe que E[X] = 7.
Ejemplo 8: para el ejemplo 5, determinar el valor esperado de la proporción de accidentes fatales.
En general, el valor esperado de una función g(x) de la variable aleatoria X, está dado por:
¾ E [g(X)] = ∑ g(x) p(x)
∞
¾ E[g(X)] = ∫ g(x) f(x) dx
-∞
si x es discreta
si x es continua
Ejemplo 9: suponga que el tiempo necesario para reparar una pieza de equipo, en un proceso de
manufactura, es una variable aleatoria cuya función de densidad de probabilidad es:
1/5 e – x/5
x>0
f(x) =
0
para cualquier otro valor
si la pérdida de dinero es igual al cuadrado del número de horas necesario para llevar a cabo la
reparación, se debe determinar el valor esperado de las pérdidas por reparación.
En este caso es necesario calcular el valor esperado de una función que se encuentra relacionada
con la variable aleatoria (el tiempo de reparación). Esta función es:
g(x) = x2,
La esperanza de una variable aleatoria X no es una función de X sino un número fijo y una
propiedad de la distribución de probabilidad de X. Por otra parte, el valor esperado puede no
existir dependiendo de si la correspondiente suma o integral no converge en un valor finito.
Ejemplo 10: Un inversionista dispone de $100.000 para una inversión de un año. El inversionista
está considerando dos opciones: colocar el dinero en el mercado de valores, lo que le garantiza una
ganancia anual fija del 15% y un plan de inversión cuya ganancia anual puede considerarse como
una variable aleatoria cuyos valores dependen de las condiciones económicas que prevalezcan.
Basándose en la historia pasada del segundo plan, un analista muy confiable ha determinado los
posibles valores de la ganancia y calculado sus probabilidades, de acuerdo a la tabla.
Ganancia (%)
30
25
20
15
10
5
Probabilidad
0.20
0.20
0.30
0.15
0.10
0.05
Con base en la ganancia esperada, ¿cuál de los dos planes debe seleccionarse?.
Propiedades.
¾ E[c] = c, donde c es una constante.
¾ E[aX + b] = aE[X] + b, donde a, b constantes.
¾ E[g(X) + h(X)] = E[g(X)] + E[h(X)]
3.5.
Momentos de una variable aleatoria.
Los momentos de una variable aleatoria X, son los valores esperados de ciertas funciones de X.
Estos forman una colección de medidas descriptivas que pueden emplearse para caracterizar la
distribución de probabilidad de X y especificarlas si todos los momentos de X son conocidos.
Los momentos pueden definirse alrededor de cualquier punto de referencia, pero generalmente se
definen alrededor del cero o del valor esperado de X.
Sea X una variable aleatoria. El r-ésimo momento de X alrededor del cero se define por:
¾ µ ’ r = E [X r] = ∑ x x r p(x)
si x es discreta
∞
¾ µ ’ r = E [X r] = ∫ x r f(x) dx
si x es continua
-∞
El primer momento alrededor de cero es la media
o valor esperado de la variable aleatoria X y se
denota por µ ; de esta manera se tiene que µ = µ ’ 1 = E [X].
Sea X una variable aleatoria. El r-ésimo momento central o momento alrededor de la
media de X, se define por:
¾ µ r = E [X – µ ] r = ∑ x (x – µ ) r p(x)
si X es discreta
∞
¾ µ r = E [X – µ ] r = ∫ (x – µ ) r f(x) dx
si X es continua
-∞
Veamos que ocurre con los primeros momentos centrales de cualquier variable aleatoria:
µ 0 = E [X – µ ] 0 = E[1] = 1
µ 1 = E [X – µ ] 1 = E[X] – µ = 0
µ 2 = E [X – µ ] 2 = Var[X] = µ ’2 – µ 2 = σ
2
que corresponde a la Varianza de la variable aleatoria. Tal como se muestra, se puede calcular
como el segundo momento alrededor del origen menos el cuadrado de la media.
Tal como hemos visto, la varianza mide el grado de dispersión de la distribución, esto es, si la
mayor parte del área por debajo de la curva de distribución se encuentra cercana a la media, la
varianza es pequeña; si la mayor parte del área se encuentra muy dispersa alrededor de la media, la
varianza será grande. Sabemos que la raíz cuadrada positiva de la varianza recibe el nombre de
desviación estándar σ , y también permite medir el grado de dispersión de los datos, además está
expresado en la misma escala de los datos originales.
Otra medida que permite comparar loa dispersión relativa de dos distribuciones de probabilidad es
el coeficiente de variación, que está definido por:
CV = σ /µ
Este coeficiente expresa la magnitud de la dispersión de una variable aleatoria con respecto a su
valor esperado, el CV es una medida estandarizada de la variación con respecto a la media,
especialmente útil para comparar dos distribuciones de probabilidad cuando la escala de medición
difiere de manera apreciable entre éstas.
Ejemplo 11: Supongamos las variables aleatorias X e Y, que tienen los siguientes parámetros:
E(X) = 120, Var(X) = 36; E(Y) = 40, Var(Y) = 16
A pesar de que la dispersión de X es más grande que la de Y en un sentido absoluto
(Var(X) = 120 > Var(Y) = 16); la dispersión relativa de X es menor que la dispersión relativa de Y,
puesto que CVX = 0.05 < CVX = 0.10.
De la misma manera podemos analizar los momentos centrales de orden superior de una variable
aleatoria.
El tercer momento central µ 3 = E [X – µ ] 3 está relacionado con la asimetría de la distribución de
probabilidad de X. A partir del desarrollo del binomio, podemos encontrar que el término de la
asimetría es: µ 3 = µ ’ 3 – 3 µ µ ’2 + 2 µ 3 entonces, si µ 3 < 0, se dice que la distribución es
asimétrica negativa, si µ 3 > 0, se dice que la distribución es asimétrica positiva, y si µ 3 = 0, la
distribución es simétrica. Este estadígrafo presenta dos problemas: a) permite analizar la
distribuciones unimodales; b) depende de las unidades en las que se mide la variable3/2aleatoria X, en
este caso se recomienda utilizar el tercer momento estandarizado, α 3 = µ 3 /(µ 2) que recibe el
nombre de coeficiente de asimetría.
α
3
> 0 Asimetría positiva α
3
< 0 Asimetría positiva
α
3
= 0 Simétrica
El cuarto momento central µ 4 = E [X – µ ] 4 = µ ’ 4 – 4 µ µ ’3 + 6µ 2µ ’ 2 – 3 µ 4 es una medida de
que tan puntiaguda es la distribución de probabilidad y recibe el nombre de curtosis. Al igual que
en el caso del tercer momento es preferible utilizar la estandarización: α 4 = µ 4 /µ 22
si α 4 > 3, la distribución de probabilidad presenta un máximo relativamente alto y recibe el nombre
de leptocúrtica; si α 4 < 3, la distribución es relativamente plana y recibe el nombre de platicúrtic,;
y si α 4 = 3, la distribución no presenta un máximo ni muy alto ni muy plano y recibe el nombre de
mesocúrtica.
α 4 > 3 leptocúrtica
mesocúrtica
α
4
α
< 3 platicúrtica
4
=
3
el valor de 3 se utiliza como una referencia debido a que en la práctica la curtosis estandarizada de
una distribución de probabilidad se compara con la de una distribución normal, cuyo valor es tres.
Ejemplo 12. Dos vendedores de seguro de vida, A y B, visitan de 8 a 12 clientes potenciales por
semana, respectivamente. Sean X e Y dos variables aleatorias que representan el número de seguros
vendidos por A y B, como resultado de las visitas. Basándose en una gran cantidad de información
pasada, las probabilidades para los valores de X e Y son:
x
0
1
2
3
4
5
6
7
p(x) 0.02 0.09 0.21 0.28 0.23 0.12 0.04 0.01
8
0
y
0
1
2
3
4
5
6
7
p(y) 0.06 0.21 0.28 0.24 0.13 0.05 0.02 0.01
8
0
9
0
10
0
11
0
12
0
Comparar y contrastar las distribuciones de probabilidades de X e Y utilizando los estadígrafos que
sean necesarios.
Ejemplo 13. Considérese las variables aleatorias X e Y, cuyas funciones de densidad de
probabilidad son:
1/30
f(x) =
0
80 ≤ x ≤ 110
para cualquier otro valor
y
1/10.000 e (-y/10.000)
y>0
f(y) =
0
para cualquier otro valor
Determinar y comparar las distribuciones a partir de la media, varianza y los momentos
estandarizados tercero y cuarto de X e Y.
Otros estadígrafos.
Para cualquier variable aleatoria X, se define a la mediana x0.5 de X por:
P(X < x0.5) ≤ ½ y P(X < x0.5) ≥ ½
si X es discreta
P(X ≤ x0.5) = ½
si X es continua
Para cualquier variable aleatoria X, se define a la moda xm de X como el valor xm
de X que maximiza la función de probabilidad (si X es discreta), o la función de
densidad de probabilidad si X es continua
Para cualquier variable aleatoria X, se define el valor quantil xq de orden q, de X (0 <
q < 1), por:
P(X < xq ) ≤ q y P(X < xq ) ≥ q
si X es discreta
P(X ≤ xq ) = q
si X es continua
La Desviación media de una variable aleatoria X es el valor esperado de la diferencia
absoluta entre X y su media, y está dado por:
E | X – µ | = ∑ | x – µ | p(x)
si X es discreta
x
∞
E | X – µ | = ∫ | x – µ | f(x) dx
si X es continua
-∞
3.6.
Funciones Generadoras de Momentos.
Un método alternativo para determinar los momentos de una variable aleatoria dada su distribución
de probabilidad, es encontrar la esperanza de cierta función conocida como función generadora de
momentos.
Sea X una variable aleatoria. El valor esperado de e tX recibe el nombre de función
generadora de momentos, y se denota por mx(t), si el valor esperado existe para
cualquier valor de t en algún intervalo -c < t < c, en donde c es un número positivo. En
otras palabras.
m x(t) = E[ e tX ] = ∑ x e tx p(x)
si X es discreta
∞
m x(t) = E[ e tX ] = ∫ e tx f(x) dx
si X es continua
-∞
mx(t) es una función solamente de t. Si t = 0, entonces mx(0) = E(e 0) = 1. Si la función generadora
de momentos existe, puede demostrarse que es única y que determina por completo la distribución
de probabilidad de X. En otras palabras, si dos variables aleatorias tienen la misma función
generadora de momentos, entonces tienen la misma distribución de probabilidades.
Si la función generadora de momentos existe para -c < t < c, entonces existen las derivadas de ésta
de todas las ordenes para t = 0, y esto asegura que mx(t) generará todos los momentos de X
alrededor del origen.
Sea X una variable aleatoria. El valor esperado de e t(X – µ ) recibe el nombre de función
generadora de momentos central y se denota por m x-µ (t), si el valor esperado existe para
cualquier valor de t en algún intervalo -c < t < c, en donde c es un número positivo.
m x-µ (t) = E[ e t(X – µ ) ] = ∑ x e t(x – µ ) p(x)
si X es discreta
∞
m x–µ (t) = E[ e t(X – µ ) ] = ∫ e t(x – µ ) f(x) dx
si X es continua
-∞
Ejemplo 14. Sea X una variable aleatoria, cuyas función de densidad de probabilidad es:
f(x) =
1/θ e –x/θ
x>0
0
para cualquier otro valor
en donde θ es un número mayor que cero. Determinar la función generadora de momentos de X.
Ejemplo 15. Sea X una variables aleatoria discreta, con función de probabilidad:
∝
-λ
x
x = 0, 1, 2, ....
p(x) = e λ
x!
∑
x=0
en donde λ es un número mayor que cero. Determinar la función generadora de momentos de X.
3.7.
Desigualdad de Tchebyshev.
Se han estimado promedios y varianzas para diversas distribuciones de probabilidades, y hemos
visto que ambas cantidades proporcionan alguna información útil acerca del centro y dispersión de
la masa de probabilidad. Ahora, si solo se conocen estos valores, ¿se puede decir algo acerca de las
probabilidades para diversos intervalos?.
Si la distribución tiene una forma razonablemente simétrica, podemos decir que ≅ 68% de las
observaciones están ± 1 desviación estándar de la media (µ– σ , µ+ σ ), y ≅ 95% de las
observaciones están ± 2 desviación estándar de la media (µ – 2σ , µ + 2σ ).
Si la distribución no es tan simétrica, estos resultados no son muy buenos y puede dar una mala
aproximación; en estos casos, y en general, podemos aplicar la Desiguald de Tchebyshev que
relaciona a µ, σ y las probabilidades.
Teorema de Tchebyshev. Sea X una variable aleatoria cuya media es µ y su varianza σ 2.
Entonces para toda k positiva
P(| X – µ | < k σ ) ≥ 1 –
1
2
k
Ejemplo 16. La producción diaria de motores eléctricos en una fábrica es 120 de promedio con
una desviación estándar de 10.
a) ¿qué fracción de días serán de un nivel de producción entre 100 y 140?.
b) Calcular el intervalo más corto que con certeza contenga por lo menos el 90% de los
niveles de producción diaria.
Ejemplo 17. el costo diario por usar determinada herramienta tiene una media de $13, y una
varianza de 41. ¿con que frecuencia el costo será mayor que 30?