Descargar - Matestay Design by Carlos Estay F.

“FUCIÓ CUADRÁTICA”
La función cuadrática es una función muy común en Matemática.
Se trata de una función de segundo grado: la "x" aparece elevada al
cuadrado como máxima potencia.
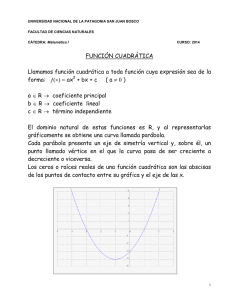
Su representación gráfica es una curva llamada “parábola”, la cual
presenta como punto característico al “vértice”. En dicho punto la función
pasa de ser creciente a decreciente o viceversa.
Su forma analítica general es:
y = a.x2 + b.x + c
Término Cuadrático
Término Lineal
Término Independiente
Para graficarla
realizamos una
tabla de valores:
ta
y
a=1
Por ejemplo: y = x2 – 4.x + 3
es
b=−4
M
at
c=3
x
y
0
3
1
0
5
2
−1
4
3
0
3
4
3
y
6
Ordenada
al origen
d2
d2
2
Eje de Simetría
x = Xv
1
0
d1
d1
1
2
3
4
6
7
8
9
x
Ceros X1 y X2
Vértice V (Xv , Yv )
Instituto Nacional
5
1/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
En esta sencilla función cuadrática, con sólo hacer una tabla de
valores hemos hallado todos los elementos característicos de la parábola: su
vértice V(2,−1), sus ceros X1 = 1 y X2 = 3, y su ordenada al origen f(0) = 3,
tal cual se muestra en la gráfica.
En adelante, desarrollaremos las fórmulas necesarias para hallar estos
elementos en una parábola cualquiera, que por lo general no son fáciles de
hallar con una simple tabla de valores.
CEROS O RAÍCES DE LA FUCIÓ CUADRÁTICA:
La función cuadrática, como toda función puede tener "ceros" o
"raíces", que son valores de la variable independiente "x" que hacen cero a
la función "y".
y = a x2 + b x + c
Función cuadrática
0 = a x2 + b x + c
Ecuación cuadrática
c
0
b
= x2 + x +
a
a
a
2
2
y
Dividimos miembro a miembro por "a"
c
 b 
 b   b 
0 = x + 2  x +  −   +
a
 2a 
 2a   2a 
Completamos
cuadrados
2
at
es
ta
2
b 
b2
c

0 = x +  − 2 +
2a  4a
a

M
b2
c
b 

−
= x + 
2
4a
a
2a 

2
b2 − 4ac 
b 
= x + 
2
4a
2a 

Despejamos "x":
2
b2 − 4ac
b
±
= x+
2
4a
2a
Fórmula Resolvente de la
Ecuación de Segundo Grado
− b ± b2 − 4ac
x1-2 =
2a
−
b
b 2 − 4ac
±
= x
2a
2a
Esta fórmula nos permite hallar las dos raíces o ceros de la ecuación
cuadrática, lo que se logra al tomar alternativamente los signos "+" y "−" de
la fórmula resolvente.
Como vemos, una parábola puede tener dos ceros reales y distintos
como en este caso, en que corta dos veces en su trayectoria real al eje "x",
en los puntos X1 y X2.
Instituto Nacional
2/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
TIPOS DE SOLUCIOES DE LA ECUACIÓ DE SEGUDO GRADO
El radicando de la fórmula resolvente, llamado discriminante
determina el tipo de soluciones que tiene la ecuación de segundo grado.
Discriminante
− b ± b 2 − 4ac
x1-2 =
2a
1) Si el discriminante es positivo:
La raíz cuadrada de un número positivo es también positiva, con lo cual
el doble signo de la raíz cuadrada lleva a dos raíces reales y distintas. La
curva cortará entonces dos veces en su trayectoria real al eje "x".
y
2) Si el discriminante es cero:
La raíz cuadrada de cero es cero, con lo cual el doble signo de la raíz
cuadrada lleva a dos raíces reales e iguales, o puede decirse una raíz real
doble. La curva tocará entonces una sola vez al eje "x" sin atravesarlo.
Puede verse que la curva "rebota" sin cruzar el eje de abscisas, o sea que
tiene su vértice sobre dicho eje.
a es (+)
b2 − 4 a c > 0
M
at
es
ta
3) Si el discriminante es negativo:
La raíz cuadrada de un número negativo no tiene resultado en el campo
real, con lo cual la solución son dos raíces complejas conjugadas. La
curva no toca en este caso al eje "x" sino que se halla siempre por arriba
o por debajo de dicho eje de abscisas.
a es (−)
y
2 Raíces Reales
y distintas
x
y
b2 − 4 a c = 0
2 Raíces Reales
e iguales
x
Instituto Nacional
3/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
y
2
b −4ac<0
2 Raíces
Complejas
Conjugadas
x
VÉRTICE
El vértice es un punto muy importante de una parábola: allí la función
cuadrática pasa de ser creciente a decreciente, teniendo un máximo la
función en ese punto; o pasa de ser decreciente a creciente teniendo un
mínimo.
La abscisa del vértice Xv es igual al
promedio de las raíces X1 y X2
at
X1 + X 2
2
M
XV =
es
ta
y
Para obtener las expresiones analíticas de las coordenadas del vértice,
es necesario tener en cuenta que las parábolas tienen un eje de simetría
vertical que pasa por dicho vértice. La existencia de un eje de simetría
implica que las dos "ramas" de la curva, a la derecha e izquierda del eje
están equidistantes respecto al mismo. Por ello:
A partir de esta expresión se puede obtener otra, que es más útil y
directa en la práctica, pues permite hallar Xv sin calcular antes las
raíces, sino a partir de los coeficientes "a" y "b" de la forma general:
X1
X2
− b + b 2 − 4ac
− b − b2 − 4ac
+
2a
2a
XV =
2
− b + b 2 − 4ac − b − b2 − 4ac
−2b 1
2a
XV =
=
. ⇒
2
2a 2
Como el vértice es un punto más de la parábola,
sus coordenadas Xv e Yv también deben
satisfacer la ecuación de la curva. Por tanto:
Instituto Nacional
4/14
XV = −
b
2a
YV = f (X v )
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
La ordenada del vértice "Yv" es el valor que toma la función "y"
cuando la variable "x" se reemplaza por el valor previamente hallado de
"Xv".
EJE DE SIMETRÍA
Otro elemento importante de la parábola es el eje de simetría, que
como sabemos es una recta vertical que pasa por vértice. Su ecuación es:
La ecuación del eje de simetría es la correspondiente a
una recta vertical del tipo: x = constante
x = Xv
Este eje se llama de simetría debido a que si trazamos cualquier recta
perpendicular al mismo, vemos que la distancia desde un punto de la curva
al eje de simetría, es igual a la distancia desde dicho eje al punto ubicado en
la otra rama. Así pues, la parábola es una curva con ramas simétricas.
ORDEADA AL ORIGE
es
La Ordenada al Origen de una parábola es igual al
término independiente "c" de la forma general.
Para Practicar
M
at
f(0) = c
ta
y
Al igual que en las rectas, la parábola tiene una ordenada al origen,
que es el valor que toma la función cuando "x" vale cero. Gráficamente
corresponde al punto donde la curva corta al eje "y".
Verificar con el Simulador Digital "Función
Cuadrática"
1) Dadas las siguientes funciones cuadráticas, encontrar todos sus
elementos significativos sin hacer tabla de valores, sino aplicando las
expresiones vistas. Graficar.
Raíces o Ceros.
Coordenadas del Vértice.
Ecuación del eje de simetría.
Ordenada al origen.
a) y = − x2 + 6 x – 8
X1 = 2, X2 = 4; V(3,1);
Eje x = 3; f(0) = −8
b)
y = x2 + 4 x
X1 = 0, X2 = −4;V(−2, −4);Eje x = −2; f(0) = 0
c)
y = − x2 + 1
X1 = −1, X2 = 1; V(0,1);
d)
y = x2 − 4 x – 5
X1 = −1, X2 = 5; V(2,−9); Eje x = 2; f(0) = −5
e) y = − x2 + 2 x − 4
Instituto Nacional
X1 y X2 ∉R;
5/14
Eje x = 0; f(0) = 1
V(1,−3); Eje x = 1; f(0) = −4
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
2
ESTUDIO DE LA FAMILIA DE PARÁBOLAS: y = a x
Ahora estudiaremos las curvas de esta familia de parábolas, en las
cuales no existe el término lineal ni el término independiente.
Para todas ellas: b = c = 0
El Vértice estará siempre en el origen, dado que:
XV = −
b
0
=−
=0
2a
2a
V (0; 0)
YV = f (X v ) = a X 2v = a . 0 = 0
y
5
y = x2
4
y=2x
2
3
y = 1/2 x2
2
1
y = −1/2 x2
2
3
4
5
es
1
at
y = −2 x2
−5 −4 −3 −2 −1 0
−1
−2
M
y = −x2
ta
y
x
−3
−4
−5
Como podemos observar, cuando el coeficiente cuadrático "a" es
positivo, las ramas van "hacia arriba" y la función tiene un mínimo en el
vértice. Por caso contrario, cuando el coeficiente "a" es negativo las ramas
van "hacia abajo" y la función tiene un máximo en el vértice.
Además vemos que cuanto mayor es el valor absoluto de "a" las ramas
"se cierran" más sobre la vertical, dando una parábola de más rápido
crecimiento o decrecimiento. Por caso contrario cuando el valor absoluto
de "a" es menor que 1, las ramas están más abiertas que en la parábola
básica y = x2, con lo que se obtiene una curva de más lento crecimiento o
decrecimiento.
Instituto Nacional
6/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
Ahora veremos que los parámetros "b" y "c" sólo desplazan la curva,
de manera que el vértice pueda estar en cualquier punto del plano, pero no
alteran la forma de la parábola, la cual depende exclusivamente de "a".
FORMA CAÓICA DE LA FUCIÓ CUADRÁTICA
Aparte de la forma general ya vista, donde la parábola queda definida
por los parámetros "a", "b" y "c", existe la llamada "forma canónica" que a
menudo es más útil, pues en la misma los parámetros son directamente las
coordenadas del vértice y el factor "a" que como vimos define la forma de
la curva.
Desplazaremos una parábola de la familia vista y = a x2 (con vértice
en el origen) a un punto cualquiera del plano de coordenada V(Xv;Yv):
y
Tomamos un sistema de
referencia auxiliar x'y':
y'
y' = a (x')2
P (x';y') ≡ (x;y)
y'
ta
y
y'
x' = x − Xv
y' = y − Yv
at
Vértice
V(Xv;Yv)
M
Yv
es
x'
y
x'
Como:
Reemplazando:
x
Xv
x
y − Yv = a (x − Xv)2
y = a (x − Xv)2 + Yv
Forma Canónica de la Parábola
FORMA FACTORIZADA DE LA FUCIÓ CUADRÁTICA
Una tercera forma de expresión de una función cuadrática es la forma
factorizada. En ella los tres parámetros que definen a la parábola son las
dos raíces X1 y X2 (cuando son reales y distintas) y el coeficiente
cuadrático "a".
Forma Factorizada de la Parábola
y = a (x − X1) (x − X2)
Es natural aceptar esta forma de expresión de la función cuadrática,
pues se verifica que cuando "x" toma el valor de las raíces X1 o X2 la
Instituto Nacional
7/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
función "y" se anula. Además tiene el coeficiente "a" que define la forma
de la curva. Quedando definida la forma y los dos ceros de la función, la
parábola queda totalmente definida.
LAS TRES FORMAS DE EXPRESIÓ DE LA PARÁBOLA
En el siguiente esquema se marcan los caminos a seguir para pasar de
una forma a otra de expresión de la parábola.
Fórmula Resolvente
Forma General
Completar Cuadrados
y = a.x2 + b.x + c
Desarrollo
de Cuadrado
de Binomio
Propiedad
Distributiva
Forma Factorizada
Forma Canónica
y − Yv = a (x − Xv)2
y = a (x − X1) (x − X2)
ta
y
X + X2
XV = 1
2
YV = f ( X V )
es
Verificar con el Simulador Digital "Función
Cuadrática" y sus simuladores adicionales
“Forma Canónica” y “Forma Factorizada”
M
at
Para Practicar
1) Dadas las siguientes funciones cuadráticas, expresarlas en las restantes
formas; Graficar.
a) y = − x2 + 6 x – 8
y = − (x – 3)2 + 1
y = − (x − 2) (x – 4)
b) y = x2 + 4 x
y = (x + 2)2 − 4
y = x (x + 4)
c) y = − x2 + 1
y = − x2 + 1
y = − (x + 1) (x – 1)
2
d) y = 2 (x − 2) (x + 3)
2
y = 2 x + 2 x − 12
1  25

y = 2 x +  −
2
2

e) y = − 2 (x – 4)2 + 8 y = − 2 x2 + 16 x − 24 y = − 2 (x − 2) (x – 6)
2) Para que el vértice de la parábola y = x2 se desplace al punto (3; −2) se
utiliza la expresión:
y = (x+3)2 +2
Instituto Nacional
y = (x−3)2 +2
y = (x+3)2 −2
8/14
y = (x−3)2 −2
NRAC
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
3) El intervalo de valores de “m” para que la ecuación 2mx2 − 4x + 1 = 0
tenga raíces reales y distintas es:
(−∞; 2)
4) El intervalo de valores de “k” para que la ecuación 5x2 −2kx + 20 = 0
tenga raíces complejas conjugadas es:
(−10; 10)
5) El conjunto de valores que puede tomar “n” para que la ecuación:
{1}
−nx2 + 2x − 1 = 0 tenga raíces reales e iguales es:
Por último veremos el tema de la reconstrucción de la ecuación de
segundo grado: Si se conocen las raíces de una ecuación, se trata de
encontrar una forma de expresión de la ecuación cuadrática que admita
como raíces a dichos valores.
RECOSTRUCCIÓ DE LA ECUACIÓ DE SEGUDO GRADO
ta
y
Cuando conocemos la ecuación cuadrática y queremos hallar las raíces
usamos la fórmula resolvente de la ecuación de segundo grado. Este es el
problema directo.
Problema Directo
M
at
es
Ahora plantearemos el problema inverso: se conocen las raíces de la
ecuación y se desea hallar una forma de expresión de la misma que admita
como raíces a los valores dados.
X1
a x2 + b x + c = 0
X2
Problema Inverso
Según la forma factorizada de la
ecuación cuadrática, se cumple:
Dada la forma general de la
ecuación cuadrática, se cumple:
a (x − X1) (x − X2) = 0
2
a.x + b.x + c = 0
a ( x 2 − X 2 x − X1 x + X1X 2 ) =0
b
c

a  x 2 + x +  =0
a
a

Instituto Nacional
a ( x 2 − ( X 2 + X1 ) x + X1X 2 ) =0
9/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
b
= − ( X1 + X 2 )
a
Por comparación:
c
= X1 . X 2
a
Fórmulas de la reconstrucción de la ecuación de segundo grado
Como vemos sólo hay dos coeficientes independientes en la ecuación
cuadrática, puesto que el valor de "a" tomado en forma aislada no es
importante. Generalmente se hace a = 1 al reconstruir la ecuación.
Recordemos que si a una ecuación cuadrática se la multiplica
miembro a miembro por una cierta constante se obtiene una ecuación
equivalente, lo que indica que la nueva ecuación tiene las mismas raíces X1
y X2 que la ecuación original:
2. (x2 + 5 x + 6) = 0 .2
Ecuaciones
Equivalentes
2 x2 + 10 x + 12 = 0
y
x2 + 5 x + 6 = 0
x2 +
ta
at
es
La forma:
X2 = −3
b
c
x+ =0
a
a
M
X1 = −2
Las ecuaciones
equivalentes tienen
raíces idénticas
X1 = −2
X2 = −3
se llama forma normalizada o
reducida de la ecuación cuadrática.
X1 . X2
− (X1 + X2)
Dados las raíces X1 y X2: el coeficiente lineal de la forma normalizada
es igual a la suma de las raíces cambiada de signo y el término
independiente es igual al producto de dichas raíces.
Para Practicar
Verificar con el Simulador Digital "Función
Cuadrática" y sus simuladores adicionales
“Forma Canónica” y “Forma Factorizada”
1) Dadas las raíces reconstruir las ecuaciones cuadráticas normalizadas:
a) X1 = −2 ; X2 = 3
x2 − x − 6 = 0
b) X1 = −1 ; X2 = −5
x2 + 6 x + 5 = 0
c) X1 = 0 ; X2 = −3
x2 + 3 x = 0
Instituto Nacional
10/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
2) La ecuación de segundo grado reducida (a = 1) en la variable “x”
sabiendo que una de las raíces es X1 = −2 y que el coeficiente del
término lineal es −3 es:
x2 −3x +10 = 0
x2 +3x −10 = 0
x2 −3x −10 = 0
x2 +3x +10 = 0
NRAC
3) El valor (o los valores) de “m” para que la abscisa de uno de los puntos
de intersección entre las curvas correspondientes a las funciones
y = 2x2 – m e y = 1 – 3 x sea X1 = −5 es (o son):
(m= 34)
ta
y
4) Si se restringe el dominio de la función y = −x2 + 2x −3 al intervalo
(−1; 2) la imagen es:
(−6; −2]
x2 −x −6 = 0
x2 +x +6 = 0
x2 −x +6 = 0
NRAC
M
x2 +x −6 = 0
at
es
5) La expresión de una función cuadrática que sólo es negativa en el
intervalo (−3; 2) puede ser:
6) Las temperaturas entre las 0 hs y las 24 hs en una zona rural se
1
2
ajustan por la función T ( x ) = − ( x − 12 ) + 10 , donde T es la
10
temperatura en ºC y "x" es la hora del día. Responda:
a) ¿Cuál fue la temperatura máxima?
b) ¿A que hora del día se registró?
c) ¿Qué temperatura se registra a las 3 de la tarde?
(10 °C)
(12 hs)
(9,1 °C)
7) Un cuerpo se arroja verticalmente desde una altura de 40 m. La
altura en función del tiempo está dada por: h (t ) = 40 + 30 t − 4,9 t 2 ,
donde "h" es la altura en (m) y "t" es el tiempo en (s). Responda:
a) ¿Cuál fue la altura máxima?
b) ¿En qué instante se registró?
c) ¿Cuándo vuele a tocar el suelo?
d) Graficar.
Instituto Nacional
11/14
(85,9 m)
(3,06 s)
(7,25 s)
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
Trabajo Práctico : Función Cuadrática
Dadas las siguientes funciones cuadráticas, encontrar todos sus
elementos significativos sin hacer tabla de valores, sino aplicando las
expresiones vistas. Graficar.
1)
a) y = x2 − 2 x + 3
Raíces o Ceros.
Coordenadas del Vértice.
Ecuación del eje de simetría.
Ordenada al origen.
2)
b)
y = −2 x2 − 12 x −10
c)
y = x2 + 4 x + 4
d)
y = 2 x2 − 8
e)
y = − x2 − 4 x − 3
Dadas las siguientes funciones cuadráticas, expresarlas en las
restantes formas (Canónica, Factorizada y General); Graficar.
a) y = − x2 − 2 x + 3
b) y = x2 − 2 x
at
es
e) y = 2 (x – 3)2 − 8
ta
d) y = (x − 3) (x + 1)
y
c) y = −2 x2 + 2
y = (x+5)2 +1
4)
y = (x−5)2 +1
y = (x+5)2 −1
y = (x−5)2 −1
NRAC
El intervalo de valores de “m” para que la ecuación mx2 +5x + 5 = 0
tenga raíces reales y distintas es:
(− ∞ ; −5/4]
5)
M
10.3) Para que el vértice de la parábola y = x2 se desplace al punto (−5; −1)
se utiliza la expresión:
(5/4;
∞)
(− ∞ ; 5/4)
(−5/4;
∞)
NRAC
El intervalo de valores de “k” para que la ecuación −2x2 + 5kx − 8 = 0
tenga raíces complejas conjugadas es:
(−5/8; 5/8)
Instituto Nacional
(−8/5; ∞)
(−∞; 8/5)
12/14
(−8/5; 8/5)
NRAC
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
6)
El conjunto de valores que puede tomar “n” para que la ecuación:
−x2 + nx − 4 = 0 tenga raíces reales e iguales es:
{4}
{−4, 4}
{} = ∅
{−2, 2}
NRAC
7)
Hallar el conjunto de valores que puede tomar “n” para que la
ecuación: −2x2 + 5nx + 7 = 0 tenga raíces reales e iguales.
8)
Dadas las raíces reconstruir las ecuaciones cuadráticas reducidas o
normalizadas:
a) X1 = −1 ; X2 = 5
b) X1 = 2 ; X2 = −3
c) X1 = −4 ; X2 = −1
Hallar la ecuación de segundo grado reducida (a = 1) en la variable
“x”, sabiendo que una de las raíces es X1 = 6 y que el coeficiente del
término lineal es −12.
10 )
Hallar la ecuación de segundo grado reducida (a = 1) en la variable
“x”, sabiendo que una de las raíces es X1 = −3 y que el término
independiente es 15.
11)
El valor (o los valores) de “m” para que la abscisa de uno de los
puntos de intersección entre las curvas correspondientes a las
funciones y = −x2 + 2m e y = 6 – 5 x sea X1 = 4 es (o son):
12 )
Si se restringe el dominio de la función y = x2 + 4x al intervalo
(−3; 0], hallar el conjunto imagen.
13)
La expresión de una función cuadrática que sólo es positiva en el
intervalo (1; 7) puede ser:
M
at
es
ta
y
9)
−x2 +8x −7 = 0
14 )
−x2 −8x −7 = 0 −x2 +8x +7 = 0 −x2 −8x +7 = 0
NRAC
La ganancia de una compañía se ajusta por la función cuadrática
2 000
G( p) = −
p ( p − 12 ) , donde G es la ganancia en "$" y "p"
3
es el precio en "$" a que se vende cada producto. Responda:
a) ¿Cuál es la ganancia máxima que puede obtener?
b) ¿A qué precio de venta unitario se obtiene la máxima ganancia?
c) ¿Para qué precios se llega a una situación de equilibrio?
Instituto Nacional
13/14
COMPILED by Prof. Carlos Estay Fuentes
Función Cuadrática
d) ¿Para qué precios se obtendrá una utilidad de $ 20 000?
15 )
El arco de un puente que cruza un río, se adapta a la función
1
cuadrática h ( x ) = − x ( x − 20 ) , donde "h" es la altura del arco y
20
"x" es el ancho del río, ambos en metros.
a) ¿Cuál es la altura máxima a que se elevará el arco?
b) ¿A qué distancia del margen del río alcanzará el puente la altura
máxima?
c) ¿Qué altura tendrá el arco a 5 m de la orilla?
Respuestas del trabajo Práctico "Función Cuadrática"
1)
y
V(1,2);
Eje x = 1;
V(−3, 8); Eje x = −3;
V(−2, 0); Eje x = −2;
V(0, −8); Eje x = 0;
V(−2, 1); Eje x = −2;
2)
y = − (x + 3) (x – 1)
y = x (x − 2)
y = −2 (x + 1) (x – 1)
y = (x − 1)2 − 4
y = 2 (x − 1) (x – 5)
at
es
y = − (x + 1)2 + 4
y = (x − 1)2 − 1
y = − 2 x2 + 2
y = x2 − 2 x − 3
y = 2 x2 − 12 x + 10
M
a)
b)
c)
d)
e)
f(0) = 3
f(0) = −10
f(0) = 4
f(0) = −8
f(0) = −3
ta
a) X1 y X2 ∉R;
b) X1 = −5 X2 = −1;
c) X1 = X2 = −2;
d) X1 = −2 X2 = 2;
e) X1 = −3 X2 = −1;
3)
Opción c)
11)
m=1
4)
Opción c)
12)
[−4; 0]
5)
Opción d)
13)
Opción a)
6)
7)
Opción b)
{} = ∅
14)
a)
b)
c)
d)
8)
a) x2 − 4 x − 5 = 0
b) x2 + x − 6 = 0
c) x2 + 5 x + 4 = 0
15)
5m
2
9)
x − 12 x + 36 = 0
10)
x2 + 8 x + 15 = 0
Instituto Nacional
$ 24 000
$6
$ 0 y $ 12
Para p1 = $ 3,55 y p2 = $ 8,45
14/14
COMPILED by Prof. Carlos Estay Fuentes