REGLAS DE DERIVACI´ON Y DERIVADAS INMEDIATAS f = f(x), g
Anuncio
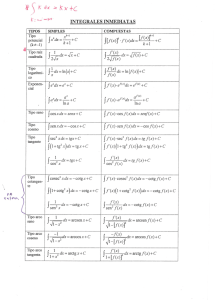
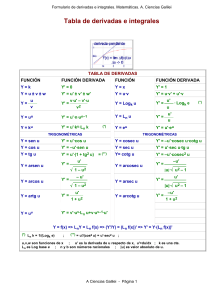
REGLAS DE DERIVACIÓN Y DERIVADAS INMEDIATAS f = f (x), g = g(x), ∂ ∂x (f ∂ ∂x (f ∂ ∂x f (x) = f 0, ∂ ∂x g(x) + g) = f 0 + g 0 = g0 Función Derivada respecto de x ax a ax ax ln(a) xm m · xm−1 ex ex ln(x) 1 x loga (x) 1 xln(a) sin(x) cos(x) cos(x) −sin(x) tg(x) cotg(x) · g) = f 0 · g + f · g 0 sec(x) ∂ f ∂x ( g ) = f 0 ·g−g 0 ·f g2 cosec(x) ∂ g ∂x (f ) 1 cos2 (x) −1 sin2 (x) = sec2 (x) = 1 + tg 2 (x) = −cosec2 (x) = −1 − cotg 2 (x) sin(x) cos2 (x) −cos(x) sin2 (x) = sec(x)tg(x) = −cosec(x)cotg(x) = (g 0 ln(f ) + f1 f 0 g)f g arcsin(x) √ 1 1−x2 arccos(x) √ −1 1−x2 arctg(x) 1 1+x2 arccotg(x) −1 1+x2 arcsec(x) √1 x x2 −1 arcsec(x) √1 x x2 −1 cosh(x) = ex +e−x 2 ex −e−x 2 = sinh(x) sinh(x) = ex −e−x 2 ex +e−x 2 = cosh(x) Nota: Cuando x sea una función f (x), en la derivada escribimos f (x) en vez de x y multiplicamos el resultado por f 0 (x) Por ejemplo, la derivada de sin(x2 ) es cos(x2 ) · 2x http://www.matesfacil.com 1
![Transforma la integral / (x2 " y2) dx ] dy a coordenadas polares y](http://s2.studylib.es/store/data/005336881_1-38107913b0406391f278007c215c7e11-300x300.png)
