FUNCION CUADRATICA

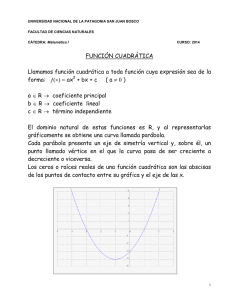
FUNCIÓN CUADRÁTICA
Sergio Signorelli
1
PROHIBIDA SU REPRODUCCION
FUNCION CUADRATICA
Anteriormente has visto la función lineal, que era de la forma y= ax + b, donde el valor
de a representaba la pendiente de la recta o lo que es lo mismo la inclinación que tenía
sobre el eje de las x, y b era el valor donde la recta cortaba al eje de las y. Esta función
se llamaba lineal porque el máximo exponente de la x era 1, y su representación gráfica
era una recta. El valor de a era muy importante pues indicaba si la recta subía
(creciente) o bajaba (decreciente).
Ahora veremos una nueva función que tiene la forma
y = ax2 + bx + c
La representación gráfica de esta función es una parábola.
Algunas gráficas de esta función son los siguientes:
Observarás que ahora el máximo exponente que tiene la x es 2, razón por la cual a la
función anterior se la llama cuadrática.
Identificaremos cada elemento de la función:
x se llama variable independiente pues el valor de la misma lo coloco yo.
y se llama variable dependiente pues justamente depende de x.
a se llama coeficiente cuadrático y es el número que acompaña a la x2.
b se llama coeficiente lineal y es el número que acompaña a la x.
c se llama coeficiente independiente y es el número que no acompaña a nadie.
Al igual que en la función lineal, el valor de a es muy importante pues nos da una idea
de cómo será gráficamente la parábola.
De este modo, si el valor de a es positivo la parábola tendrá sus ramas apuntando hacia
arriba.
FUNCIÓN CUADRÁTICA
Sergio Signorelli
2
PROHIBIDA SU REPRODUCCION
Mientras que si el valor de a es negativo las ramas apuntarán hacia abajo.
El valor de c, también es muy importante dentro de la función, pues indica adonde ha de
cortar la parábola el eje de las y (similar al valor de la b en la función lineal...)
A este valor, al de c, también se lo llama ordenada al origen.
A ver, repasemos lo visto anteriormente en un gráfico...
c
x1
x2
De acuerdo al gráfico y lo explicado anteriormente, esta parábola tiene las siguientes
características:
El valor de a deberá ser negativo pues las ramas apuntan hacia abajo
Corta el eje de las y en el valor indicado como c
Atraviesa el eje de las x en dos puntos llamados x1 y x2. Si en esos puntos corta el eje
de las x significa que el valor correspondiente al eje de las y es igual a 0. Por este
FUNCIÓN CUADRÁTICA
Sergio Signorelli
3
PROHIBIDA SU REPRODUCCION
motivo a los valores de x1 y x2 se los llama RAICES DE LA PARABOLA, y son los
puntos donde la parábola corta al eje de las x.
Para encontrar los valores de las raíces se utiliza una fórmula llamada de Bhaskara en
honor al que la determinó, y esa fórmula es aplicable a cualquier parábola escrita en la
forma y = ax2 + bx + c, pues los valores que se deben introducir en ella son los que
posee esa función.
-b+
b2 – 4 . a . c
x 1,2 =
2.a
Observemos que por ser una raíz cuadrada el término tiene dos signos, pues recordemos
que las raíces cuadradas de números positivos tienen dos soluciones, una positiva y otra
negativa.
Por ejemplo:
La raíz cuadrada de 4 es +2 y –2 porque +2 al cuadrado y –2 al cuadrado dan como
resultado 4.
(+2)2 = 4
4
(-2)2 = 4
El valor de lo que está dentro de la raíz cuadrada de la fórmula de Bhaskara es muy
importante, y se llama DISCRIMINANTE, pues justamente discrimina, determina,
indica, de que forma han de ser las raíces de la parábola.
Entonces:
b2 – 4 . a . c
DISCRIMINANTE
Este valor, obviamente, ha de ser un número, razón por la cual, tendremos tres opciones:
Que ese número sea positivo
Que ese número valga 0
Que ese número sea negativo
FUNCIÓN CUADRÁTICA
Sergio Signorelli
4
PROHIBIDA SU REPRODUCCION
Si lo escribimos con símbolos tenemos:
POSITIVO o sea que la raíz tiene dos resultados:
UNO POSITIVO Y OTRO NEGATIVO.
b2 – 4 . a . c
0 o sea que el resultado de la raíz es 0
NEGATIVO o sea que la raíz NO TIENE
RESULTADO
En el primer caso, la raíz tiene dos resultados de acuerdo a la propiedad que vimos
anteriormente, razón por la cual, las raíces x1 y x2 resultan distintas y las dos
pertenecen al conjunto de los números reales. Por este motivo la parábola atraviesa el
eje de las x en dos puntos distintos.
x1
x2
(x1 distinta de x2)
En el segundo caso, el resultado de la raíz es igual a o, razón por la cual las raíces x1 y
x2 resultan iguales pues se anula el término de la raíz y están en el conjunto de los
números reales. Por lo tanto, en este caso, la parábola rebota sobre el eje de las x.
x1 = x2
En el último de los casos la raíz no tiene resultado pues no existe ningún numero
positivo o negativo que al elevarlo al cuadrado me de cómo resultado un número
negativo. Por esta razón, en este caso, el discriminante nos indica que la parábola no
atraviesa ni rebota en el eje de las x.
NO CORTA NI REBOTA EN EL EJE x
FUNCIÓN CUADRÁTICA
Sergio Signorelli
5
PROHIBIDA SU REPRODUCCION
Bien, podemos graficar ahora una función cuadrática cualquiera e identificar cada uno
de los puntos vistos anteriomente.
xv
yv
VERTICE
O sea que identificamos el corte al eje y, y los cortes al eje x.
También hemos identificado un punto llamado VERTICE en el cual las ramas cambian
de sentido (viniendo desde la derecha van bajando y cuando llegan al vértice comienzan
a subir...).
Este punto tiene dos coordenadas, una sobre el eje x, llamada xv (x del vértice), y otra
sobre el eje y, llamada yv (y del vértice)
El vértice es otro punto importante de la parábola pues indica el punto a partir del cual
las ramas cambian de sentido y además, que por encima de ese punto o por debajo del
mismo NO HAY MÁS PARÁBOLA.
Función 1
Función 2
En el caso de la función 1, las ramas apuntan hacia arriba es decir que el valor de a es
positivo, y vemos que el vértice es el menor punto que la parábola posee en su parte
inferior, por lo tanto:
SI a ES POSITIVO EL VERTICE DE LA PARÁBOLA REPRESENTA UN
PUNTO MINIMO DE LA MISMA (por debajo de ese punto no hay más parábola).
SI a ES NEGATIVO EL VERTICE DE LA PARÁBOLA REPRESENTA UN
PUNTO MAXIMO DE LA MISMA (por encima de ese punto no hay más parábola).
Otra observación importante es que LA COORDENADA X DEL VERTICE SE
ENCUENTRA ENTRE MEDIO DE LAS DOS RAÍCES, y QUE POR ELLA
FUNCIÓN CUADRÁTICA
Sergio Signorelli
6
PROHIBIDA SU REPRODUCCION
PASA UN EJE IMAGINARIO QUE DIVIDE A LA PARABOLA EN DOS
PARTES IGUALES. ESTE EJE SE LLAMA EJE DE SIMETRÍA Y SIEMPRE
PASA POR LA XV.
Para calcular las coordenadas del vértice tendremos las siguientes ecuaciones:
Para la x del vértice:
xv = - b
2.a
conociendo los valores de a, b y c
o bien
xv = x 1 + x 2
2
conociendo los valores de las raíces x1 y x2
Para determinar la y del vértice no habrá más que reemplazar en la fórmula de la
parábola el valor obtenido de xv, por lo tanto:
yv = a . (xv)2 + b . (xv) + c
Formas de expresión de la Función Cuadrática
Ya vimos que a una función cuadrática podemos averiguarle las raíces, el vértice y
también conocer los valores de a, b y c.
Ello nos permite escribir la función cuadrática en tres formas, que son:
Si conocemos los valores de a, b y c la escribimos en la forma que ya vimos y se llama
POLINOMICA.
y = a . x2 + b . x + c
Si conocemos las coordenadas del vértice se escribe en otra forma que se llama
CANONICA
y = a . (x - xv)2 + yv
Si conocemos las raíces la podemos escribir de otra forma que se llama
FACTORIZADA.
FUNCIÓN CUADRÁTICA
Sergio Signorelli
7
PROHIBIDA SU REPRODUCCION
y = a . (x – x1) . (x – x2)
Observemos que:
1- obviamente en todas las expresiones aparece el valor de a.
2- En el caso de la canónica la xv se encuentra restando, razón por la cual debemos
tener cuidado al escribirla PUES EL VALOR DE XV QUE OBTUVIMOS
CAMBIA DE SIGNO. La yv NO CAMBIA SU SIGNO. Por ejemplo, si
2
nuestra xv = -4 y la yv = 5 la expresión queda: y = a . (x + 4) + 5
3- Idéntico razonamiento se sigue en el caso de la factorizada con las raíces.
Cuando escribimos la expresión DEBEMOS TENER LA PRECAUCIÓN DE
CAMBIAR DE SIGNO LAS RAÍCES. Por ejemplo si x1 = 4 y x2 = -2 la
expresión nos queda:
y = a . (x – 4) . (x + 2)
IMPORTANTE
SI TENEMOS UNA EXPRESIÓN DE LA PARÁBOLA EN FORMA
FACTORIZADA, LAS RAÍCES DE LA MISMA SON LOS NÚMEROS DE LA
EXPRESIÓN CAMBIADOS DE SIGNO.
y = a . (x – 5) . (x + 1)
x1= +5
x2= -1
SI TENEMOS UNA EXPRESIÓN DE LA PARÁBOLA EN FORMA
CANÓNICA, LA COORDENADA X DEL VÉRTICE DE LA MISMA ES EL
NÚMERO DE LA EXPRESIÓN CAMBIADO DE SIGNO. LA Y DEL
VERTICE SE MANTIENE IGUAL
y = a . (x - 4)2 - 7
xV= +4
yV= -7
FUNCIÓN CUADRÁTICA
Sergio Signorelli
8
PROHIBIDA SU REPRODUCCION
Pasaje de expresiones de una forma a otra
Para pasar de una forma a las otras solamente es necesario aplicar las fórmulas
vistas anteriormente y/o propiedades matemáticas como la distributiva.
Ejemplo 1: a partir de la polinómica y = 3x2 + 4x + 1 hallar la factorizada y la
canónica.
Primero hallamos las raíces:
Y ahora escribimos la forma factorizada:
Luego hallamos las coordenadas del vértice:
Y escribimos la forma canónica:
Ejemplo 2: a partir de la canónica y = 3 (x+4)2 - 1 hallar la factorizada y la
polinómica.
En primer lugar debemos resolver la parte de la función que se encuentra elevada al
cuadrado. (si no nos acordamos de la definición del cuadrado de un binomio
podemos hacer ese paréntesis multiplicado por si mismo dos veces...)
Una vez determinada la polinómica, procedemos como lo que se ha visto
anteriormente.
APLICACIONES DE LAS FUNCIONES CUADRATICAS
Las aplicaciones de la funciones cuadráticas son muchas y variadas.
Es mejor verlo con un ejemplo.
Un grupo de biólogos introdujo en un lago artificial un conjunto de peces para
estudiar su evolución. En un principio la colonia crece reproduciéndose
normalmente, pero al cabo de unos meses algunos peces mueren debido al
hacinamiento. Si la ley de evolución esta dada por la función N(x) = 240 +10x –
0,1x2 donde N es el número de peces y x el tiempo transcurrido en días, responder:
(a) ¿Cuántos peces introdujeron en el lago? (b)¿Durante cuanto tiempo la cantidad
de peces fue aumentando? (c)¿Cuál fue la cantidad máxima que llego a haber? ¿En
que momento? (d)¿Cuándo se extinguirá esa población?
En este caso, ya nos expresan la función cuadrática, de lo contrario, si no la
hubiésemos tenido, deberíamos haberla buscado utilizando cualquiera de la formas
vistas anteriormente.
FUNCIÓN CUADRÁTICA
Sergio Signorelli
9
PROHIBIDA SU REPRODUCCION
Como ya nos dieron la función, entonces vamos a graficarla, primero ordenándola:
N(x) = –0,1x2 +10x + 240
En primer lugar vemos que el valor de a es negativo, por lo tanto las ramas apuntan
hacia abajo.
Obtengamos las raíces:
Obtengamos el vértice:
Sabemos que corta el eje y en + 240, por lo tanto podemos hacer un gráfico
aproximado de la siguiente forma:
(colocar los valores obtenidos...)
+ 240
Traten de contestar ahora las preguntas planteadas, con la sola observación del
gráfico.
En otros casos, es probable que deba hacerse un planteo extra para poder conocer la
ecuación cuadrática, que obviamente dependerá de la situación que se trate.
FUNCIÓN CUADRÁTICA
Sergio Signorelli
10
PROHIBIDA SU REPRODUCCION
PROPIEDADES DE LAS RAÍCES
Las raíces de la función cuadrática tienen dos propiedades importantes que se
refieren a la suma y el producto entre ellas, y son:
x 1 + x 2=
-b
a
x 1 . x 2=
c
a
ECUACIONES CUADRATICAS
Todo lo que vimos anteriormente también es aplicable a las denominadas
ecuaciones cuadráticas, que por supuesto tendrán un término cuyo máximo grado
(exponente de la x) sea cuadrático.
Resolver estas ecuaciones es muy sencillo ya que lo único que debemos hacer es
igualar la misma a 0 haciendo todos los pasajes de términos que correspondan, para
de este modo, a través de la formula resolvente de Bhaskara obtener los resultados
que la anulen (raíces), es decir, las soluciones de la ecuación.
ANALISIS DE LOS INTERVALOS DE CRECIMIENTO O DECRECIMIENTO
DE UNA PARABOLA
Ya vimos que el vértice es un punto de inflexión de la parábola, esto es, a partir del
vértice las ramas cambian de sentido.
Esto genera un análisis de cómo crece (sube) o decrece (baja) la parábola a medida
que venimos desde la izquierda del eje x (es decir desde el menos infinito) hacia la
derecha del mismo eje (es decir hacia el mas infinito…).
Todos los valores de crecimiento o decrecimiento los vamos a tomar en relación al
eje x, razón por la cual entonces, nuestra referencia ha de ser el valor de la xv, ya
que como dijimos es en el vértice cuando las ramas de la parábola cambian de
sentido.
Veamos el siguiente gráfico:
xv
yv
Si “venimos caminando” junto a la parábola desde la izquierda, vemos que una rama
de la misma viene bajando, decreciendo, y esto se mantiene hasta que llegamos a la
FUNCIÓN CUADRÁTICA
Sergio Signorelli
11
PROHIBIDA SU REPRODUCCION
x del vértice. Allí, en el valor de la x del vértice, la rama cambia de sentido, por lo
que si “seguimos caminando” junto a la parábola ahora vemos que la rama sube, es
decir crece.
Entonces, de esta forma podemos expresar los intervalos de crecimiento y/o
decrecimiento:
Dec: desde el menos infinito hasta el valor de la xv
(que se escribe así…)
(-  ; xv]
Crec: desde la xv hasta el mas infinito
(que se escribe así…)
[xv ; +  )
Si por ejemplo tuvieses los siguientes gráficos, escribí los intervalos de crecimiento
y decrecimiento de las parábolas indicadas;
4
-6
3
2
De la misma forma podemos analizar cuando la parábola toma valores positivos y
cuando negativos. Esto es lo que se denomina CONJUNTOS DE POSITIVIDAD y
NEGATIVIDAD.
Para que se entienda mejor. La parábola tendrá VALORES DE y POSITIVOS
(IMÁGENES POSITIVAS) cuando se encuentre POR ARRIBA DEL EJE x,
mientras que tendrá VALORES DE y NEGATIVOS (IMÁGENES NEGATIVAS)
cuando se encuentre POR DEBAJO DEL EJE x.
En este caso vemos que los puntos que indican los cambios de la parábola de arriba
hacia abajo o viceversa SON LAS RAICES, es decir, que EN EL CORTE DE LA
PARABOLA AL EJE x SE PRODUCE QUE LA PARABOLA CAMBIE DE
ARRIBA HACIA ABAJO DEL EJE x O AL REVES.
FUNCIÓN CUADRÁTICA
Sergio Signorelli
12
PROHIBIDA SU REPRODUCCION
Veamos entonces estas situaciones:
x1
x2
Si “venimos recorriendo” la parábola desde la izquierda, vemos que hasta llegar a la
raíz señalada como x1 la misma se ENCUENTRA DEBAJO DEL EJE X. Una vez
que atravesamos ese valor, LA PARABOLA SE ENCUENTRA ENCIMA DEL EJE
x, y luego de atravesar la raíz señalada como x2 LA PARABOLA VUELVE A
ESTAR POR DEBAJO DEL EJE x.
Entonces, hasta que llegamos a x1 viniendo SIEMPRE DESDE LA IZQUIERDA, la
parábola TIENE VALORES NEGATIVOS DE y, lo que también ocurre cuando nos
alejamos hacia la derecha a partir de la raíz x2. Eso marca LA NEGATIVIDAD DE
LA PARABOLA, por lo que el conjunto de negatividad será:
C - Se escribe así y se dice CONJUNTO DE NEGATIVIDAD…
C - = (-  ; x1) U (x1 ; -  )
tramos…)
(la U significa UNIDO, UNION, y es la unión de ambos
Por el contrario, el CONJUNTO DE POSITIVIDAD estará entre las dos raíces, por
lo tanto será:
C + = (x2 ; x1)
Resumiendo:
La positividad o negatividad de la parábola SE EXPRESA SIEMPRE EN
FUNCION DE LAS RAICES DE LA MISMA, RESPETANDO QUE
SIEMPRE SE VIENDE DESDE LA IZQUIERDA HACIA LA DERECHA.