Usted decide empezar a bucear, y necesita comprar un tanque de

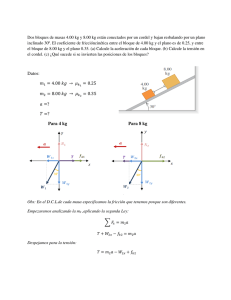
Primer Parcial Física 1 (FI01)
Nombre:
7 de mayo de 2016
CI:
Licenciatura:
Ejercicio 1
Usted decide empezar a bucear, y necesita comprar un tanque de aire apropiado. En la tienda ofrecen tanques de
aire puro comprimido (=255kg/m3, 78% N2, 21% O2, 1% otros) de 8L, 12L, 17L y 25L. Usted no quiere comprar un
tanque más grande que lo necesario, ya que eso implica bucear con más peso, por lo que decide hacer unas pruebas.
En ellas, determina que usted respira aproximadamente una vez cada 2s, y cuando lo hace inhala unos 400mg de O2.
Suponga que en cada respiración, consume todo el O2 que inspira, y que no es seguro consumir más de 2/3 del O2 en
el tanque ¿Cuál es el tanque de aire más apropiado para bucear durante 45min?
Empecemos por calcular el oxígeno consumido durante 45min de buceo. Sabemos que cada 2s consumimos 400mg
de oxígeno, por lo que consumimos en promedio 200mg de oxígeno por segundo. Como 45min corresponden a
2700s, el consumo de oxígeno en ese tiempo es de 540 000mg, o 0,54Kg.
Llamemos al oxígeno onsumido cO2 = 0,54Kg.
Pero además, no es seguro consumir más de 2/3 del oxígeno en el tanque, por lo que el tanque que compremos
deberá tener una masa de oxígeno de
mO2 = (3/2)*cO2 = 0,81Kg.
El aire en el tanque es aire puro, y consiste por lo tanto de 21% de oxígeno. Si debe haber una masa mO2 de oxígeno
en el tanque, la masa total de aire en el tanque debe ser de
maire = mO2/0,21 = 3,85Kg.
Podemos ahora calcular el volumen que 3,85Kg de aire puro comprimido ocupará, sabiendo que en ese estado, la
densidad del aire es = 255Kg/m3.
Como la densidad se define por  = m/V, entonces
V = m/ , y por tanto Vaire = maire/ = 1,51×10-2 m3 = 15,1L.
Para ir a bucear durante 45min, es necesario llevar un volumen de aire mínimo de 15,1L. Dados los tanques que
nos ofrecen y nuestro interés de llevar el más liviano posible, elegimos finalmente el tanque de 17L.
Primer Parcial Física 1 (FI01)
Nombre:
7 de mayo de 2016
CI:
Licenciatura:
Ejercicio 2
El bloque B con masa de 5,00 kg descansa sobre el bloque A,
cuya masa es de 8,00 kg, y el cual a la vez, se encuentra sobre
una mesa horizontal. No hay fricción entre el bloque A y la
mesa, pero el coeficiente de fricción estática entre el bloque A y
el B es de 0,750. Una cuerda ligera atada al bloque A pasa por
una polea sin masa ni fricción, con el bloque C colgando en el
otro extremo.
a) Realice el diagrama de cuerpo libre de cada uno de los
bloques.
b) Escriba las ecuaciones de movimiento para los tres bloques,
suponiendo que el bloque B desliza respecto al A.
c) ¿Qué masa máxima puede tener el bloque C, de modo que A y B aún se deslicen juntos cuando el
sistema se suelte del reposo?
a) Diagramas de cuerpo libre
NAB
aB
NBA
FAB
aA
T
T
FBA
mB.g
mA.g
N
aC
mC.g
Se indican también las aceleraciones (aunque esto no es necesario).
b) Pares de acción y reacción: NBA y NAB: normal de superficie entre A y B.
FAB y FBA fuerza de rozamiento entre la superficie A y B.
Leyes de Newton de los 3 cuerpos (suponiendo que desliza B sobre A). Esto implica que la aceleración
del cuerpo A y B son distintas.
Cuerpo B-
eje x:
mB.aB= FBA
eje y: 0 = NBA - mB.g
Cuerpo A-
eje x:
mA.aA= T-FAB
eje y: 0 = N- NAB - mA.g
Cuerpo C-
eje y: mC.aC= mC.g - T
Además se cumple: aA = aC (ya que la cuerda no se estira), NAB= NBA (son pares de acción y
reacción) y la fuerza de rozamiento cinético:
=
=
c) Se supone ahora que A y B no deslizan, por tanto todos los cuerpos tendrán la misma aceleración, a
la que llamaremos simplemente a.
Si A y B no deslizan, se comportan como un solo cuerpo de masa A+B
La segunda ley de Newton para este cuerpo en el eje x: (
y sobre el cuerpo C:
=
−
⇒
=( − )
(2)
Sustituyendo en (1): (
) =( − )
+
⇒
=
+
(
)
) =
(1)
(3)
Tenemos que calcular cuál es la máxima aceleración que puede imprimir la fricción estática al cuerpo
B.
=
=
Sustituyendo en (3):
=
(
)
=
=
por tanto la máxima aceleración vale:
=
(
)
=
=
(
)
=
(
)
=
( ,
,
( ,
)( ,
)
.
)
=39,0 kg
=39,0 kg (expresado con 3 cifras significativas como corresponde).
Primer Parcial Física 1 (FI01)
7 de mayo de 2016
Nombre:
CI:
Licenciatura:
Ejercicio 3
Una partícula de masa m parte del reposo desde el punto más alto de una esfera sólida sin rozamiento,
de radio R y va resbalando por su superficie. Si los ángulos θ se miden a partir de la vertical,
encuentre:
a) La energía potencial en función del ángulo θ.
b) La energía cinética en función de la velocidad angular dθ/dt .
c) Determine la reacción normal sobre la partícula, en función del ángulo (utilice la conservación de la
energía mecánica para eliminar θ).
d) El ángulo para el cual la partícula se despega de la superficie de la esfera.
a) Partícula de masa m, desliza sin fricción. v0=0
Considero que energía potencial vale cero en el punto más alto.
=− ℎ=−
(1 − cos )
b) Como suponemos que la energía mecánica vale cero en el punto de partida,
la energía cinética + la potencial debe ser nula en cualquier punto
=− =
(1 − cos )
c) Según la dirección radial, la segunda ley de Newton:
−
=
( ) = 3
( )−
cos
cos − 2

=
( )=
cos −
(3 cos − 2)
=
cos −
( )=
= cos
= 48,19º
cos −
(3 cos − 2)
d) El ángulo en el que se desprende es aquel en que N=0.
( ) = 0 ⇒ 3 cos − 2 = 0
=
(
)
Primer Parcial Física 1 (FI01)
Nombre:
7 de mayo de 2016
CI:
Licenciatura:
Ejercicio 4
La fotografía muestra dos jugadores de Rugby en el
momento en que el jugador de la derecha taclea al de la
izquierda. Inicialmente el jugador de la izquierda estaba
inmóvil y el otro lo embiste con una velocidad de 7,50 m/s.
Ambos deportistas tienen masas muy similares.
a) Estime la velocidad del centro de masas de ambos
jugadores antes de la embestida.
b) ¿Qué velocidad tendrían en el momento en que se tomó la
foto?
En ambas partes enuncie las hipótesis que utiliza para simplificar el análisis y justifique las ecuaciones
utilizadas.
De acuerdo a la foto los dos jugadores están en el aire y parece ser un
instante después que el jugador de la derecha tacleó al de la izquierda.
Tomaremos entonces la foto como un instante después del tackle.
V0
Antes del
contacto
Supondremos que ambos jugadores se comportan como si fueran
partículas.
Momento
del tackle.
Modelo a utilizar:
Inmediatamente
después del
contacto
F12
F21
Vf
Suponemos que
en este instante
fue tomada la foto
Durante el contacto las fuerzas de interacción entre los jugadores son muy
grandes comparadas con las fuerzas externas. Estas son interacciones de los jugadores con el piso, el aire y
la gravitatoria.
De acuerdo al modelo la cantidad de movimiento del sistema formado por los dos jugadores se conserva
un instante antes y un instante después del choque. Entonces, la velocidad del centro de masas es la
misma un instante antes y un instante después del contacto (más allá de ese pequeño lapso es necesario
considerar el peso y la trayectoria de los jugadores ya comenzaría a ser una parábola)
Ecuaciones:
m1v1  m2 v2 
mv  mv2 v1  v2 0  7, 5m/s

m1  m1   vCM  1


 3,8m/s vCM  3,8m/s
2
m
2
2

m1  m2  m

Como la velocidad del CM es la misma antes y después del choque, tenemos que la velocidad de ambos
vCM 
deportistas en el momento de la foto es v  3,8m/s