Cálculo Integral - Aprende Matemáticas

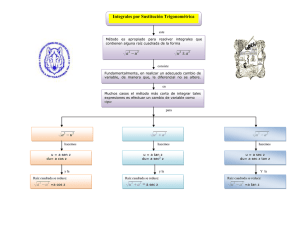
Profr. Efraín Soto Apolinar.
Integración por sustitución trigonométrica
En esta sección vamos a estudiar el primer método para integrar funciones que no son inmediatamente integrables a partir de la tabla de integrales que tenemos.
Las siguientes sustituciones sirven para simplificar el integrando a una forma inmediatamente
integrable:
Para:
√
√
√
a2 − b2 u2
Sustituir:
a
u = sin z
b
para obtener:
a
a2 + b2 u2
u=
a
tan z
b
a
b2 u2 − a2
u=
a
sec z
b
a
p
√
√
1 − sin2 z
=
a cos z
1 + tan2 z
=
a sec z
sec2 z − 1
=
a tan z
Debes recordar siempre sustituir dx a partir del cálculo correspondiente para que la diferencial
quede en términos de dz.
En el apéndice del libro se encuentran las definiciones básicas de las funciones trigonométricas y
las identidades más frecuentemente usadas.
Calcula la siguiente integral:
Z √
9 − 4 x2
dx
x
Ejemplo 1
• Empezamos observando que a2 = 9, lo cual implica que a = 3, y b2 = 4, es decir, b = 2.
• Entonces hacemos: x = ( a/b) sin z:
x=
3
sin z
2
⇒
dx =
3
cos z dz
2
• Sustituyendo estos valores en la integral obtenemos:
s
2
3
√
9−4
sin z
Z
Z
2
9 − 4 x2
3
dx =
cos z dz
3
x
2
sin z
2
• Ahora podemos simplificar dentro del signo de raíz:
s
2
3
9
−
4
sin
z
Z
2
3
cos z dz
=
3
2
sin z
2
=
Z p
Z
www.aprendematematicas.org.mx
3
9 − 9 sin2 z
cos z dz
sin z
p
1 − sin2 z
cos z dz
sin z
1/8
Profr. Efraín Soto Apolinar.
• Pero 1 − sin2 z = cos2 z,luego,
Z p
1 − sin2 z
3
cos z dz
sin z
=
=
=
• Ahora podemos integrar:
Z √
9 − 4 x2
dx
x
cos z
cos z dz
sin z
Z
cos2 z
3
dz
sin z
Z
1 − sin2 z
3
dz
sin z
Z 1
3
− sin z dz
sin z
= 3
Z
1
dz − 3 sin z dz
sin z
Z
3 csc z dz + 3 cos z
= 3
=
Z
Z
= 3 ln | csc z − cot z| + 3 cos z + C
• Hasta aquí hemos obtenido un resultado parcial.
• Recuerda que inicialmente la integral estaba dada en términos de x, no de z.
• Por lo que nosotros debemos dar el resultado en términos de x.
• Para lograr eso, vamos a representar geométricamente la sustitución inicial:
x=
3
sin z
2
⇒
sin z =
2 x Cateto opuesto
=
3
Hipotenusa
• En el triángulo rectángulo tenemos1 :
3
z
√
2x
9 − 4 x2
• Por la forma como se definen las funciones trigonométricas a partir de un triángulo rectángulo tenemos:
√
√
9 − 4 x2
9 − 4 x2
3
csc z =
,
cos z =
y
cot z =
2x
3
2x
1 Para
calcular el cateto adyancente al ángulo z hemos utilizado el teorema de Pitágoras.
www.aprendematematicas.org.mx
2/8
Profr. Efraín Soto Apolinar.
• Entonces, podemos reescribir la solución como:
Z √
9 − 4 x2
dx = 3 ln | csc z − cot z| + 3 cos z + C
x
!
√
√
3
9 − 4 x2 9 − 4 x2
= 3 ln −
+C
+3
2 x
2x
3
3 − √9 − 4 x 2 p
= 3 ln + 9 − 4 x2 + C
2x
Observa que hemos utilizado un artificio: como la integral no se puede integrar de manera
inmediata debido a la forma que tiene, sabiendo que puede transformarse a una forma inmediatamente integrable usando una sustitución trigonométrica, vamos a utilizar la transformación sugerida
en la tabla dada en la página 1.
Después de hacer la sustitución obtenemos una integral en términos de funciones trigonométricas
que se puede integrar usando la variable z.
Para regresar este resultado a términos de x, utilizamos la sustitución que tomamos de la tabla
para representarla geométricamente usando un triángulo rectángulo y las definiciones de las funciones trigonométricas en él.
La integral
Z
√
x dx
9 x2 − 4
Ejemplo 2
se puede resolver a través de la regla de integración (iv). Utiliza sustitución trigonométrica para
calcularla y después la regla (iv) para verificar el resultado.
• De acuerdo a la tabla de sustituciones para este tipo de integrales, haremos:
x=
2
sec z
3
⇒
dx =
2
sec z tan z dz
3
• Ahora sustituimos estos valores en la integral para transformarla:
2
2
sec z
sec z tan z dz
Z
Z
x dx
3
3
s √
=
2
9 x2 − 4
2
9
sec z − 4
3
=
=
• Pero,
√
sec2 z − 1 =
Z
√
√
sec2 z tan z dz
√
4 sec2 z − 4
Z
4 sec2 z tan z dz
√
9 2 sec2 z − 1
4
9
Z
tan2 z = tan z, luego
x dx
2
=
2
9
9x −4
Z
sec2 z tan z dz
2
=
tan z
9
Z
sec2 z dz =
2
tan z + C
9
• Ahora vamos a reescribir el resultado en términos de x.
www.aprendematematicas.org.mx
3/8
Profr. Efraín Soto Apolinar.
• El triángulo rectángulo que representa la sustitución que hicimos al principio del problema
es el siguiente:
√
3x
9 x2 − 4
z
2
• Entonces, de acuerdo a este triángulo, tenemos:
√
9 x2 − 4
tan z =
2
• Y al sustituir este valor en el resultado de la integral obtenemos:
√
√
Z
x dx
2 9 x2 − 4
9 x2 − 4
√
+C =
+C
=
9
2
9
9 x2 − 4
• Ahora vamos a verificar el resultado usando la regla (iv):
• Para este fin, definimos: v = 9 x2 − 4. Entonces, dv = 18 x dx. Luego x dx =
Z
√
x dx
=
9 x2 − 4
=
=
dv
.
18
1
1 v1/2
dv
√ =
v−1/2 dv =
·
+C
18
18 1/2
18 v
1/2
1 2 2
9x −4
+C
·
18
√ 1
9 x2 − 4
+C
9
Z
Z
• Y terminamos.
Calcula la integral:
Z
Ejemplo 3
√
dx
16 x2 + 25
• Usaremos la sustitución:
x=
5
tan z
4
⇒
dx =
5
sec2 z dz
4
www.aprendematematicas.org.mx
4/8
Profr. Efraín Soto Apolinar.
• Esto transforma la integral a:
Z
√
dx
16 x2 + 25
Z
=
5
4
=
tan z2 + 1 =
Z
√
√
√
sec2 z dz
25 tan z2 + 25
5
sec2 z dz
√
4 5 tan z2 + 1
Z
1
sec2 z dz
√
4
tan z2 + 1
=
√
Z
Z
=
• Pero
5
sec2 z dz
4
s 2
5
16
tan z + 25
4
sec2 z = sec z, luego,
dx
16 x2 + 25
=
1
4
Z
1
sec2 z dz
=
sec z
4
Z
sec z =
1
ln |sec z + tan z| + C
4
• Para hacer el cambio a la variable x usamos el siguiente triángulo rectángulo:
2
x
√ 16
+
25
4x
z
5
• Entonces, haciendo las sustituciones de acuerdo a la definición de las funciones trigonométricas en el triángulo rectángulo obtenemos:
√
Z
16 x2 + 25 4 x dx
1
√
= ln +
+C
2
4
5
5 16 x + 25
Calcula la siguiente integral:
Z √
1 − 25 x2
dx
x2
Ejemplo 4
• Usaremos la sustitución:
x=
1
sin z
5
⇒
dx =
1
cos z dz
5
www.aprendematematicas.org.mx
5/8
Profr. Efraín Soto Apolinar.
• Al sustituir estos valores en la integral obtenemos:
s
Z √
1 − 25 x2
dx
x2
=
=
=
=
1
sin z
5
2
1
sin z
5
2
1 − 25
Z
1
cos z dz
5
p
1 − sin2 z
(cos z dz)
2
sin
z
Z
cos z
5
cos z dz
sin2 z
Z
cos2 z
5
dz
2
Z sin z
Z
= 5
5
cot2 z dz
• Ahora utilizaremos la identidad: cot2 z = csc2 z − 1:
Z
Z √
1 − 25 x2
dx
=
5
cot2 z dz
x2
Z = 5
csc2 z − 1 dz
= 5
Z
csc2 z − 5
Z
dz
= −5 cot z − 5 z + C
• Ahora calculamos los valores de z y cot z en términos de x a partir del triángulo rectángulo
correspondiente:
1
z
sin z =
√
5x
= 5x
1
5x
1 − 25 x2
⇒
z = arcsin(5 x )
√
1 − 25 x2
cot z =
5x
• Ahora sustitumos estos valores en el valor de la integral:
Z √
1 − 25 x2
dx = −5 cot z − 5 z + C
x2
!
√
1 − 25 x2
= −5
− 5 arcsin(5 x ) + C
5x
√
1 − 25 x2
= −
− 5 arcsin(5 x ) + C
x
www.aprendematematicas.org.mx
6/8
Profr. Efraín Soto Apolinar.
Es importante recordate que la integral inicial estaba dada en términos de la variable x.
Si entregas un resultado en términos de z, en realidad tu resultado no es incorrecto, pero tampoco
es correcto. Simplemente está incompleto.
Debes expresar el resultado en términos de la variable que aparezca la integral inicial. Por eso
se requiere hacer el cambio de variable dos veces: La primera para poder hacer la integral, la
segunda para entender el resultado.
Calcula la siguiente integral:
Z
x2
dx
√
dx
x2 − 4
Ejemplo 5
• Hacemos:
x = 2 sec z
⇒
dx = 2 sec z tan z dz
• Sustituyendo estos valores en la integral obtenemos:
Z
dx
√
dx =
x2 x2 − 4
=
=
=
=
=
• Dado que x = 2 sec z, se sigue: sec z =
Z
2 sec z tan z dz
√
4 sec2 z 4 sec2 z − 4
Z
sec z tan z dz
√
2 sec2 z sec2 z − 1
Z
tan z dz
sec z tan z
Z
dz
sec z
1
2
1
4
1
4
Z
1
cos z
4
1
sin z + C
4
x
.
2
• El triángulo que corresponde para hacer el cambio de variable de z a x es:
√
x
x2 − 4
z
2
√
• Entonces, sin z =
x2 − 4
, y la integral queda:
x
Z
dx
√
dx =
2
x
x2 − 4
√
x2 − 4
+C
4x
www.aprendematematicas.org.mx
7/8
Profr. Efraín Soto Apolinar.
Créditos
Albert
Einstein
Todo debe hacerse tan simple como sea posible, pero no más.
Este material se extrajo del libro Matemáticas I escrito por Efraín Soto Apolinar. La idea es compartir estos trucos para que más gente se enamore de las matemáticas, de ser posible, mucho más
que el autor.
Autor: Efraín Soto Apolinar.
Edición: Efraín Soto Apolinar.
Composición tipográfica: Efraín Soto Apolinar.
Diseño de figuras: Efraín Soto Apolinar.
Productor general: Efraín Soto Apolinar.
Año de edición: 2010
Año de publicación: Pendiente.
Última revisión: 07 de agosto de 2010.
Derechos de autor: Todos los derechos reservados a favor de Efraín Soto Apolinar. México. 2010.
Espero que estos trucos se distribuyan entre profesores de matemáticas de todos los niveles y sean
divulgados entre otros profesores y sus alumnos.
Este material es de distribución gratuita.
Profesor, agradezco sus comentarios y sugerencias a la cuenta de correo electrónico:
[email protected]
www.aprendematematicas.org.mx
8/8