Ecuaciones cartesianas de las cónicas

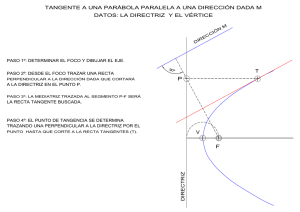
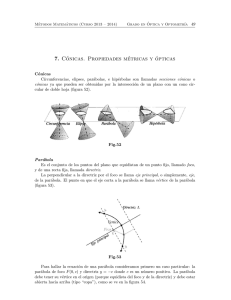
Ecuaciones cartesianas de las
cónicas
Salvador Olivares Campillo
#
Índice General
1 Elipse
1
2 Parábola
2.1 Ejemplo: movimiento en un campo uniforme y constante . . . . . . . . . . . . . .
3
3 Hipérbola
5
C B 4
U
1
Recordemos que cada punto de una cónica dista de un
punto fijo (foco) e veces lo que le separa de una recta
dada (directriz). Parece natural tomar el origen en el foco y uno de los ejes paralelo a la directriz, pero entonces
no se obtienen, con la definición de cónica, las ecuaciones
cartesianas más sencillas. Sin embargo, basta trasladar
el origen para conseguirlas. Trasladaremos, pues, los ejes
cartesianos y el origen será otro punto O0(x0O , 0), dependiendo de la curva. Las nuevas coordenadas de cualquier
punto serán x0 = x − xO0 e y 0 = y.
1
Elipse
El nuevo origen es el punto medio del eje mayor, que tiene
x = −ae. Por tanto:
1. Para el foco, x0 = 0 − (−ae) = ae.
J
C B U
2
2. La directriz se transforma en la recta x0 = a/e. En
efecto, x = r0(1 + 1/e) = r0(e + 1)/e = a(1 − e)(e +
1)/e = a(1 − e2)/e (hemos tenido en cuenta que el
semieje mayor es a = r0/(1 − e)), y
1 − e2
a
a
+ ae = .
e
e
3. La definición de cónica toma la forma
p
(x0 − ae)2 + (y 0 − 0)2 = e(a/e − x0).
Elevando al cuadrado esta última ecuación, simplificando y reordenando, resulta
x02(1 − e2) + y 02 = a2(1 − e2),
que, con b2/a2 = 1 − e2, conduce a
x02 y 02
+ 2 = 1,
a2
b
(1)
J
C B U
3
después de dividir por el cuadrado del semieje menor.
Evidentemente, esta ecuación de la elipse se transforma
en la de la circunferencia si hacemos a = b = R:
x2 + y 2 = R 2 .
2
(2)
Parábola
Trasladaremos el origen al vértice (x = r0) y, además,
invertiremos el eje de las x (cambiando el signo), con lo
que todas las abscisas de los puntos de la parábola serán
positivas. Con esto:
1. La nueva abscisa del foco es x0 = r0.
2. La directriz es la recta x0 = −r0.
3. La definición de parábola (e = 1) se escribe
p
(x0 − r0)2 + (y 0 − 0)2 = x0 + r0.
J
C B U
4
Después de elevar al cuadrado y simplificar, la última ecuación da la que buscamos:
y 02 = 4r0x0.
(3)
Evidentemente, si cambiamos los nombres tendremos
otras formas, por ejemplo, con y 0 = x, x0 = y y 4r0 = 1/c
es y = cx2.
2.1
Ejemplo: movimiento en un campo uniforme y
constante
Demuéstrese que el movimiento de una partı́cula en el
campo uniforme y constante de la gravedad es parabólico
(g es la aceleración de la gravedad). ¿Cuál es el radio
de curvatura en el punto más alto de la trayectoria de un
cuerpo lanzado formando un ángulo con la horizontal?
J
C B U
Solución
5
3
Hipérbola
Ya sabemos que con e > 1 hay puntos que cumplen la
definición de cónica en los dos lados de la directriz (la
hipérbola tiene dos ramas). Queremos la ecuación cartesiana que tiene el origen en el punto medio entre sus dos
vértices. Por semejanza con la elipse, llamaremos 2a a
la distancia de vértice a vértice, y empezaremos encontrándola.
El primer vértice es el que tiene x = r0; el segundo,
al otro lado de la directriz, debe cumplir x = e(x −
r0(1 + 1/e)) (por la definición de cónica). Despejando,
encontramos que la abscisa de este segundo vértice es
x = r0(e + 1)/(e − 1). Por tanto,
r0
e+1
−1 =2
.
2a = r0
e−1
e−1
J
C B U
6
Trasladamos, pues, el origen al punto del eje de
x = r0 + a = a(e − 1) + a = ae,
y:
1. La abscisa del foco se convierte en la x0 = 0 − ae =
−ae.
2. La recta de la directriz es la x0 = r0(1 + 1/e) − ae =
−a/e.
3. Para los puntos a la derecha de la directriz, la distancia
a ella es x0 − (−a/e) = x0 + a/e; para los que están a
su izquierda, −a/e − x0. La igualdad de la definición
de cónica la vamos a elevar al cuadrado, como hemos
hecho antes con la elipse y la parábola, y la forma
de los cuadrados de las distancias a la directriz es la
misma. Por tanto, la siguiente ecuación es válida para
J
C B U
7
las dos ramas de la hipérbola:
(x0 + ae)2 + y 02 = e2(x0 + a/e)2.
Simplificando la ecuación anterior, tenemos
x02(e2 − 1) − y 02 = a2(e2 − 1).
Llamando b2 a a2(e2 − 1), y dividiendo por esta área, resulta, finalmente,
x02 y 02
− 2 = 1.
a2
b
(4)
J
C B U