3.3 La derivada

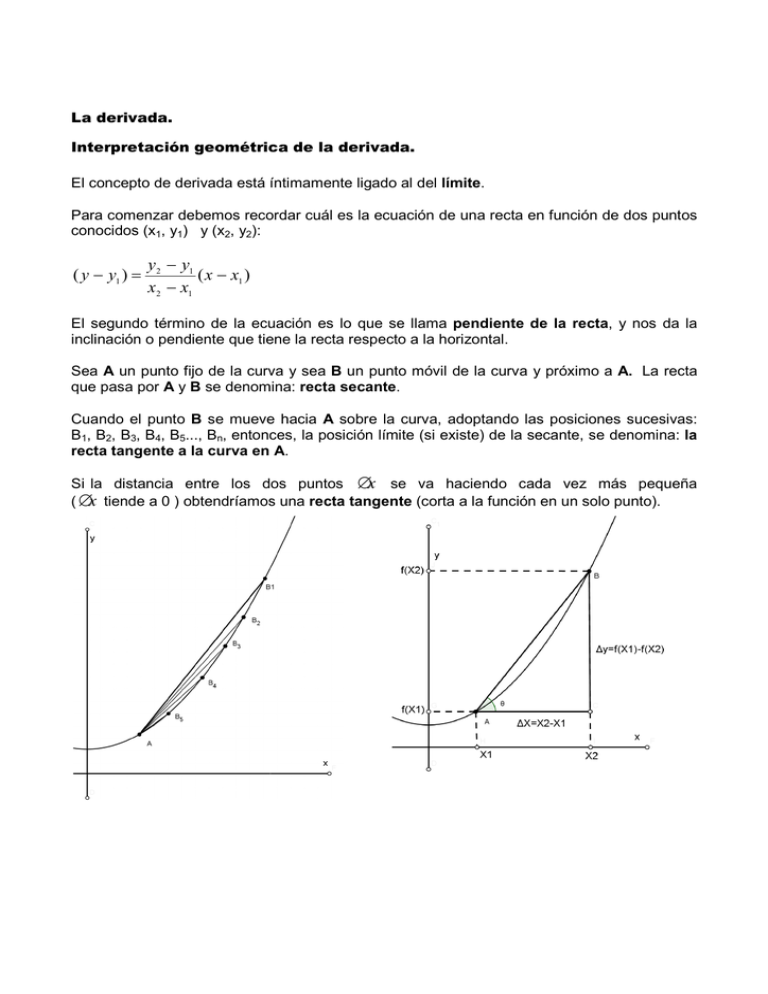
La derivada.
Interpretación geométrica de la derivada.
El concepto de derivada está íntimamente ligado al
a del límite.
Para comenzar debemos recordar cuál es la ecuación de una recta en función de dos puntos
conocidos (x1, y1) y (x2, y2):
( y − y1 ) =
y 2 − y1
( x − x1 )
x2 − x1
El segundo término de la ecuación es lo que se llama pendiente de la recta,
recta y nos da la
inclinación o pendiente que tiene la recta respecto a la horizontal.
Sea A un punto fijo de la curva y sea B un punto móvil de la curva y próximo a A. La recta
que pasa por A y B se denomina: recta secante.
Cuando el punto B se mueve hacia A sobre la curva, adoptando las posiciones sucesivas:
B1, B2, B3, B4, B5..., Bn, entonces, la posición límite (si existe) de la secante, se denomina: la
recta tangente a la curva en A.
Si la distancia entre los dos puntos ∆x se va haciendo cada vez más pequeña
( ∆x tiende a 0 ) obtendríamos una recta tangente (corta a la función en un solo punto).
punto
Ahora, si las coordenadas de los puntos A y B son respectivamente:
A(x1, f(x1)) y B(x2, f(x2)) entonces, la pendiente de la recta secante AB , denotada por
msec AB es:
msec AB = tan θ =
∆x = x 2 − x1
f ( x2 ) − f ( x1 )
Pero como:
∆x
Si despejamos x2.
x2 = x1 + ∆x
f ( x 2 ) = f ( x1 + ∆x ) Por lo tanto:
. msec AB = tan θ =
f ( x1 + ∆x) − f ( x1 )
∆x
¿Qué sucede cuando “ ∆x ” se hace tan pequeño que tiende a cero?
La recta secante se transforma en una recta tangente.
En consecuencia, la recta tangente a la curva en el punto A (si no es vertical), es la recta
cuya pendiente viene dada por:
mtg =
lim f ( x1 + ∆x) − f ( x1 )
= Derivada.
∆x → 0
∆x
Pues bien a la pendiente de la recta tangente se le llama derivada ( f ′) de la función en
ese punto:
f ′( x1 ) =
lim f ( x1 + ∆x) − f ( x1 )
∆x → 0
∆x
De esta forma, la ecuación de la recta tangente a la curva en A(x1, f(x1)) es:
y − f ( x1 ) = f ' ( x1 )( x − x1 )
Derivación de funciones algebraicas utilizando fórmulas.
Antes de iniciarse en el cálculo de las derivadas deberemos de tener las siguientes
consideraciones:
Las primeras letras del abecedario son consideradas como constantes
las últimas letras como variables , , , , , .
, , , , , ;
1
=0
La derivada de un constante es cero.
2
=1
La derivada de una variable con respecto a ella
misma es1.
+
La derivada de varios términos que se estén
sumando o restando es igual a la derivada de
cada uno de ellos respetando su signo.
3
4
−!
= #
&
5
='
=
+
!
La deriva de una constante (c) que multiplica a
una variable (v), es igual a la constante
multiplicada por la derivada de lo que le
llamamos variable.
$
&()
−
#
$
La derivada de una variable (v) elevada a un
exponente (n), es igual al exponente multiplicado
por la variable,
al exponente menos 1,
multiplicado por la derivada de lo que llamamos
variable.
Derivada de funciones algebraicas utilizando las primeras 5 fórmulas.
Ejemplos resueltos.
Hallar la derivada de las siguientes funciones.
En los siguientes ejemplos se detalla el procedimiento para su solución, dentro del círculo se
específica el número de la fórmula empleada en cada renglón.
1) y=3
*+
*,
=
**,
y´ = 0
2) y=x
---------------
1
*+
*,
=
*,
*,
/′ = 1
--------------
2
,
3) y= 6x
*+
*,
=
*0,
*,
4) y= x+7
--------------
*+
4
*,
*,
*,
=
-
6)y=
*, 5
*,
------------
*+
5
*,
/′ = 3
-() *,
2 3---------*,
/′ = 3
6
1 ----------
=
-
*4
*,
+4
*, 5
*,
*+
*,
=
6
6
-
1
<
5
* ,<
*,
6
/′ = 2
-
*,
*,
6
-
/′ =
/′ =
/′ =
6
-
=
<
* ,
*,
2
2
3
) *,
6 *,
6() *,
2 3$
*,
/′ = 3
6
+ 4:5
)
6
4
1
+
3 2
6
+
)
6
4
1
2
*+
1 -----------2
*,
5
2
=
6
6
8
4
5
--
7() *,
2*,3$-----
1 ;---------
+4 5
8
=3
2
5
2
6
8
+ 20
6
+2 3
1 + 1
6
+6 +1
*?, <
*,
/′ = 9 2
3
*, 9
1 + 4 #5
y= 9
1 + -----------------+
1
2
+ 4 2 *, 3--------
6
y= 3
3
-----------
3 + 2 3--------
2
---
---------
/′ = 3
8) y= 3 + 1
6
+
*, <
/′ = #2
)
+
3
7
*8, 9
+
/′ = / ′ = 3
7) y=
--------
-() *,
2*,3
/′ = 3
2
6
/′ = / ′ = 3
+
*,
/′ = 1
/′ = 6 1 = 6
*+
*,
/′ = 1 + 0-----------
*,
/′ = 6 2 3------------2
5) y=
=
+
*, <
*,
/′ = 9 #2
/′ = 9 2
*0,
*,
+
*)
*,
---------
*,
3 + 6 2 3 + 0-------*,
6() *,
2*,3$
+ 6 1 -----
1 + 6-------- 2
/ ′ = 18 + 6
3
4
5
1
2
9) y=
y= 4
10) /
8
,5
(-
/
/′
4
42
(-
*, B5
*,
3----------------
4
/′
4# 3
/′
4: 3
(8
/′
4
3
12
(8
(8
1 ;------------
5
quedando como:
-
5
()
<
/′
-
=
<
6
6
3
2
*,
2*,3------------- 5
1 -------------
2
)
6
Representamos la potencia como radical.
-<
/′
regresamos x-4 al denominador
12
/′
/′
/′
2
-
representamos al radical como
potencia.
6
/
(-() *,
2 3$-------*,
/′
/
pasamos x3 al numerador como x-3
√
5
<
8
6
√
)
finalmente queda como:
3√
2
/′
Derivada de funciones algebraicas utilizando las primeras 5 fórmulas, la fórmula 6 y 7.
6
* D E
*E
*D
2 3
*,
2 3
*,
2 3
7
*,
Ejemplos resueltos.
2
3
6
2
3
Hallar la derivada de las siguientes funciones.
1) y=(x)(x+3)
2) y= (2x2)(x-1)
Consideremos a u=x y v=x+3.
Consideremos a u=2x2 y v=x-1
GH
(x) 2
*,
y’=(x)I2 3
y′
x
*,
1
* ,G*,
3
3 2 3
*
2 5 3J
*,
0
x
y’= x + x + 3 = 2x + 3
y’=2x+3
*,
3
3 1
2
1
*,
6
3
2
*:6, < ; ,()
/′
*,
/′
2
2
2
y’= 2
y’= 2
y’= 2
y’= N
6
2
6
1
6
1
#
*,
*)
*,
*,
0
6
O
4
+ 4x
*, <
1 L2 2
1 L2 #2
1 2 :2 1 ;
6
6
3
6
1 4
+ 4x
2
1 L
$
2
*,
6
3M
M
6
3
6() *,
2 3$M
*,
4
1, 2 y 5
H
y=
O
Consideremos a u=x y v=x+2
*+
*,
/′
/′ =
P
*2
3
PQ<
*,
2 2
3−
+2
+2 1 −
+2
6
/′ =
+2 −
+2
/′ =
6
+2−
=
+2 6
+
6
/′ =
2
2
3
/′
7
3
2
3
=
R
RP< BSP
:, < (8,;2 5 Q < P 3( -,G6 #
$
RP
RP
, < (8, <
6
6
-
−4
2
+
−4
20 + 2
6,
7
6
3− 3 +2 #
6
−4
6
3 − 3 + 2 22
6
−4
6
1,4
6()
3
8,
−
2
$
3−4
5,4
6
−4
6
−4
2 1
− 3 +2 2
6 −4 6
)
1 −4 1
2 − 3 +2 2 −4
6 −4 6
6
2 − 8 − 6 6 + 4 − 12 − 8
/′ =
6 −4 6
6
2 −8 −6 6+8 +8
−4 6 + 8
′
/ =
= 6
6 −4 6
−4 6
/′ =
6
Consideremos a u=3+2x y v=x2-4x
1
/′ =
1
2
+2
/′ =
=
2
+2 − 1+0
+2 6
+2
2
-G6,
, < (8,
2