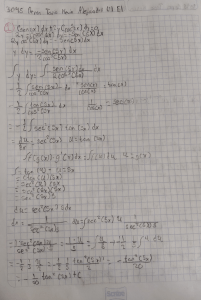Temario para el Examen Final

Formulario para el 2o Examen Parcial de Ecuaciones Diferenciales
Reducción de orden
Fórmula para la segunda solución
Caso I : No contiene y
y ′ = z ; y ′′ = z ′
∫
y 2 ( x ) = y1 ( x )
Caso II : No contiene x
y′ = z
y ′′ = z
;
dz
dy
Ecuaciones Lineales Homogéneas de
Coeficientes Constantes
II)
III)
y h = c1e
mx
y h = c1e
αx
u1′ =
2
+ c2 xe
∫
− P ( x )dx
y1
2
⋅dx
Método de Variación de Parámetros
I) y h = c1e m x + c 2e m x
1
e
mx
u2′ =
cos βx + c 2 eαx senβ x
− fy2
W
fy1
W
Algunos ejemplos de la forma de proponer yp dependiendo de yh para el enfoque
de superposición del Método de Coeficientes Indeterminados
g(x)
yp(x) propuesta
g(x)
yp(x) propuesta
-16
A
-35cos(4x)
Asen(4x)+Bcos(4x)
5x+7
Ax + B
47e5x
A e5x
3x2-2
A x2+Bx+C
(7x2-3) e5x
(A x2 +Bx +C) e5x
2x3-5x+7
A x3+B x2+Cx+D
-5 x2cos(4x)
(A x2+Bx+C)cos(4x)+(D x2+Ex+F)sen(4x)
6sen(4x)
Asen(4x)+Bcos(4x)
3x e5x cos(4x)
(Ax+B) e5x cos(4x)+(Cx+D) e5x sen(4x)