PRIMER PRINCIPIO (segunda parte)

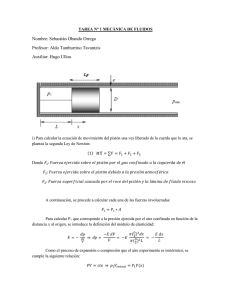
PRIMER PRINCIPIO DE LA TERMODINÁMICA (SEGUNDA PARTE)
Roberto Laura
(versión preliminar)
Introducción.
En las secciones anteriores presentamos el primer principio de la termodinámica, para
un sistema físico con las siguientes características:
a) está formado por un número muy grande de pequeñas partículas masivas
(¿moléculas?)
b) las partículas se mueven obedeciendo las leyes de la mecánica clásica.
c) cada par de partículas interacciona con fuerzas débilmente atractivas a distancias
grandes, y muy repulsivas a distancias cortas. Estas fuerzas son conservativas, de modo
que hay una energía potencial asociada a cada interacción entre pares de partículas.
d) sobre cada una de las partículas actúan también fuerzas externas.
Obtuvimos entonces la siguiente expresión:
⎛1
2 ⎞
(1)
Δ⎜ MVCM
⎟ + ΔU = W + Q ,
⎝2
⎠
donde M es la masa total del sistema, VCM es la velocidad de su centro de masa, U es
la energía interna, W es el trabajo realizado sobre el sistema, y Q es el calor que entra
al sistema.
Destaquemos que la “deducción” del primer principio de la termodinámica que hemos
desarrollado se ha basado exclusivamente en los conceptos de la mecánica clásica. No
hemos tenido en cuenta en la deducción la presencia de los campos electromagnéticos, y
tampoco hemos considerado la teoría cuántica, hoy considerada como la teoría
fundamental, y de la que la mecánica clásica es solo una aproximación.
Equivalente mecánico del calor. Experimento de Joule.
En la presentación que hicimos del primer principio, el trabajo de las fuerzas externas
sobre el sistema se consideró como la suma W + Q . El símbolo W designa al trabajo
“ordenado” que puede escribirse como una fuerza por un desplazamiento macroscópico,
tal como el que aparece cuando se desplaza un pistón en el cilindro de un motor. El
símbolo Q representa al trabajo “desordenado”, tal como el que realizan las moléculas
del metal de una pava al fuego sobre las moléculas del agua contenida en ella.
Es evidente de estas definiciones de W y de Q , que se trata de cantidades que
representan distintas formas de transferirle energía a un sistema, y que ambas cantidades
pueden expresarse en unidades de energía, como el Joule ( J = N ⋅ m ). Pero antes del
siglo ¿? se consideraba al calor como una sustancia (el calórico), que fluía de los
cuerpos a temperatura elevada hacia los cuerpos a temperatura más baja. El calor tenía
entonces su propia unidad, la caloría, que se definía como la cantidad de “sustancia
calórico” que debía entregarse a un gramo de agua para que eleve un grado su
temperatura.
Fue Joule quien en ?? realizó experimentos para determinar el equivalente mecánico del
calor, es decir para contabilizar cuanta energía debía entregarse a un gramo de agua de
modo de producir el efecto de una caloría, es decir para elevar un grado su temperatura.
El dispositivo experimental consiste en un recipiente aislado térmicamente, que
contiene una masa m de agua. Como se ve en la figura, un eje vertical giratorio tiene
paletas que están sumergidas en el agua. En su parte superior, el eje tiene un tambor en
1
el que está arrollada una cuerda. Esta cuerda, después de pasar por una polea, tiene
atada en su otro extremo un bloque de masa M , sujeta a una altura H sobre el piso.
Cuando se suelta el bloque, este desciende la altura H , haciendo girar las paletas dentro
del agua. En este giro, las paletas hacen sobre el agua un trabajo W = MgH . Como las
paredes del recipiente son buenos aislantes térmicos, podemos considerar que no ingresa
calor al recipiente en el proceso ( Q = 0 ). Además, durante el proceso el centro de masa
del agua no cambia de lugar.
Teniendo todo esto en cuenta podemos usar la ecuación (1) para obtener la siguiente
expresión para la variación de energía interna del agua
ΔU = MgH
En este proceso de entrega de trabajo al agua, esta experimenta un aumento de
temperatura ΔT , que se puede medir en el termómetro que está sumergido en el agua.
Como por definición, una caloría es la cantidad de calor para que un gramo de agua
aumente un grado su temperatura, esta variación de energía interna se puede escribir
también en la forma
1cal
ΔU =
⋅ m ⋅ ΔT
gr⋅º C
Igualando las dos expresiones para la variación de energía interna obtenemos
1cal
⋅ m ⋅ ΔT = MgH .
gr⋅º C
De aquí deducimos que
M ⋅H
m
1cal =
⋅ 9,8 2 ⋅10 −3 kg ⋅º C
m ⋅ ΔT
s
Las cantidades m , M , H y ΔT se pueden medir en el experimento, y se obtiene
entonces
1cal = 4,18 J ,
(2)
que es la expresión de la caloría en Joules, la unidad de energía del sistema
internacional.
Trabajo sobre un fluido.
2
Consideremos un fluido (líquido o gas), dentro de un recipiente como el que indica la
figura.
Se trata de un cilindro de paredes rígidas con un émbolo móvil. Supongamos que con
una fuerza externa representada por el vector Fext , y aplicada sobre el émbolo, se
produce un pequeño desplazamiento del mismo, representado por el vector Δl . El
pequeño trabajo realizado sobre el fluido resulta entonces
ΔW = F ext ⋅ Δl =| F ext | ⋅ | Δl | .
Si con A designamos al área del émbolo en contacto con el fluido, podemos escribir
| F ext |
ΔW =
⋅ A | Δl |= − pext ⋅ ΔV .
(1)
A
En la expresión anterior pext es la presión exterior, es decir la fuerza por unidad de área
que el émbolo hace sobre el fluido, y ΔV es la variación del volumen ocupado por el
fluido, cuando el émbolo se desplaza como indica la figura. El signo negativo
corresponde ponerlo para que el trabajo externo resulte positivo cuando el volumen
disminuye ( ΔW > 0 si ΔV < 0 ).
Si la fuerza externa va cambiando a medida que se modifica el volumen ocupado por el
fluido, podemos considerar ese proceso como una sucesión de pequeños cambios de
volumen en que el trabajo se escribirá como en la ecuación (1). El trabajo total en el
proceso será la suma de estos trabajos pequeños. Si se conoce como es la presión
externa en función del volumen, el trabajo se puede obtener con la siguiente integral.
V final
W =−
∫p
ext
(proceso general)
(V ) dV
(3)
Vinicial
Esta última expresión depende de la presión exterior aplicada, y será válida para
cualquier tipo de proceso que experimente el fluido, sea pasando por sucesivos estados
de equilibrio o no (procesos reversibles o irreversibles).
Si el proceso se realiza lentamente, de modo que el fluido pase por sucesivos estados de
equilibrio, resultará que la presión externa se iguala en todo momento a la presión en el
interior del fluido ( pext = p fluido ), y podemos escribir entonces
V final
W =−
∫p
fluido
(proceso reversible).
(V ) dV
Vinicial
3
(4)
El primer principio para un proceso infinitesimal reversible de un fluido.
La expresión (1) toma la siguiente forma especial para un proceso reversible
infinitesimal
⎛1
2 ⎞
d ⎜ MVCM
⎟ + dU = δW + δQ .
⎝2
⎠
En esta expresión la letra d indica el diferencial, o pequeño incremento de una función
de estado del sistema. Así por ejemplo dU es el diferencial de la energía interna U ,
que es una función de estado, una propiedad del sistema termodinámico. En cambio, las
cantidades δW y δQ no designan diferenciales. El sistema termodinámico no
“contiene” calor Q ni trabajo W , o en otras palabras no hay ninguna propiedad
termodinámica del sistema que podamos denominar Q ó W . Las cantidades δW y δQ
se usan entonces para designar cantidades muy pequeñas de trabajo y de calor que
ingresan al sistema.
Si se trata de un fluido en un proceso infinitesimal reversible, hemos visto que
δW = − pdV , de modo que podemos escribir
⎛1
2 ⎞
(5)
d ⎜ MVCM
⎟ + dU = − pdV + δQ .
⎝2
⎠
Calores específicos y molares.
Para un sistema macroscópicamente en reposo ( VCM =0), la cantidad de calor que es
necesario entregarle para que cada unidad de masa eleve un grado su temperatura, se
denomina calor específico.
Si el sistema tiene una masa M , y cuando recibe una cantidad de calor δQ aumenta su
temperatura una cantidad dT , su calor específico se puede escribir en la siguiente forma
δQ
.
(6)
C esp =
M ⋅ dT
Para el caso particular de un fluido en reposo, la ecuación (5) permite escribir
δQ = dU + pdV , y resulta entonces
dU + pdV
C esp =
.
(7)
M ⋅ dT
Que en el numerador de esta última expresión aparezcan dos diferenciales sumados es
un indicio de que el calor específico dependerá de la forma en que se realice el proceso
de entrega de calor al sistema. Hay dos casos especialmente importantes, que son
cuando este proceso se realiza a volumen constante o a presión constante. Los
correspondientes calores específicos los designaremos con CVesp y C pesp .
Según la ecuación (7), para el caso a volumen constante resulta dV = 0 , y entonces
1 ⎛ ∂U ⎞
CVesp =
(8)
⎜
⎟
M ⎝ ∂T ⎠V
En la expresión anterior (∂U / ∂T )V indica que se debe expresar la energía interna U en
función de las dos variables termodinámicas V y T ( U = U (T , V ) ), y se debe hacer a
esta función su derivada parcial respecto de la variable T . En lenguaje matemático,
queremos decir que
4
⎛ ∂U ⎞
⎛ U (T + ΔT , V ) − U (T , V ) ⎞
⎜
⎟ ≡ lim ⎜
⎟
ΔT
⎝ ∂T ⎠V ΔT →0⎝
⎠
Usando también la ecuación (7) podemos encontrar una expresión para el calor
específico cuando el proceso de calor se hace a presión constante
1 ⎛ dU + pdV ⎞
1 ⎡⎛ ∂U ⎞
⎛ ∂V ⎞ ⎤
(9)
C pesp =
⎟ ⎥.
⎟ + p⎜
⎟ =
⎜
⎢⎜
M⎝
dT
⎝ ∂T ⎠ p ⎦⎥
⎠ p M ⎣⎢⎝ ∂T ⎠ p
Para calcular esta última expresión es necesario conocer como son la energía interna U
y el volumen V en función de las variables temperatura y presión ( U = U (T , p) y
V = V (T , p) ). En la ecuación anterior (∂U / ∂T ) p y (∂V / ∂T ) p designan a las siguientes
derivadas parciales
⎛ U (T + ΔT , p) − U (T , p) ⎞
⎛ ∂U ⎞
⎟,
⎟ ≡ lim ⎜
⎜
Δ
T
→
0
ΔT
⎠
⎝
⎝ ∂T ⎠ p
⎛ V (T + ΔT , p) − V (T , p) ⎞
⎛ ∂V ⎞
⎟.
⎟ ≡ lim ⎜
⎜
Δ
T
→
0
ΔT
⎠
⎝
⎝ ∂T ⎠ p
Otra cantidad importante que necesitaremos es el denominado calor molar, que es la
cantidad de calor que es necesario entregar a un mol de una sustancia determinada para
que aumente un grado su temperatura. Si al entregar una cantidad de calor δQ a n
moles de una sustancia se obtiene un aumento de temperatura dT , el calor molar es
δQ
(10)
C molar =
n ⋅ dT
Comparando las expresiones (6) y (10), vemos que la inversa del numero de moles n
aparece en el calor molar, en vez de la inversa de la masa M que aparecía en el calor
específico. Nos damos cuenta entonces que para obtener los calores molares a volumen
constante y a presión constante, basta con que en las expresiones (8) y (9)
reemplacemos la masa por el número de moles. Obtendremos entonces
1 ⎛ ∂U ⎞
(11)
CVmolar = ⎜
⎟
n ⎝ ∂T ⎠V
1 ⎡⎛ ∂U ⎞
⎛ ∂V ⎞ ⎤
C pmolar = ⎢⎜
(12)
⎟ + p⎜
⎟ ⎥.
n ⎣⎢⎝ ∂T ⎠ p
⎝ ∂T ⎠ p ⎦⎥
Calores molares para el gas ideal.
Las derivadas parciales que aparecen en las expresiones (11) y (12) de los calores
molares para un fluido, se pueden calcular para el caso en que el fluido se comporte
como un gas ideal. En ese caso disponemos de la ecuación de estado
pV = nRT ,
y de la siguiente expresión para la energía interna
l
U = nRT ,
2
donde l es aproximadamente 3 ó 5 según que el gas sea monoatómico o biatómico.
De esta expresión para la energía interna resulta
l
⎛ ∂U ⎞ ⎛ ∂U ⎞
⎟ =⎜
⎟ = nR ,
⎜
⎝ ∂T ⎠V ⎝ ∂T ⎠ p 2
y de la ecuación de estado, escrita en la forma V = nRT / p , se obtiene
5
nR
⎛ ∂V ⎞
.
⎜
⎟ =
p
⎝ ∂T ⎠ p
Reemplazando estas derivadas parciales en las ecuaciones (11) y (12) resulta
l
⎛l
⎞
(13)
CVmolar = R,
C pmolar = ⎜ + 1⎟ R .
2
⎝2 ⎠
Este resultado es muy fuerte: nos dice que los calores molares de los gases a baja
densidad dependen solamente del número de átomos que componen su molécula, y no
de su composición. Así, de acuerdo a la teoría que hemos desarrollado en el curso, gases
monoatómicos como el ¿???, ¿??, y el ¿??, con l = 3 , debieran tener los mismos CVmolar y
C pmolar . También, gases biatómicos como el ¿?, ¿? y el ¿?, con l = 5 , debieran tener los
mismos calores molares a presión y a volumen constantes. Es notable que estas
predicciones teóricas se confirmen razonablemente bien cuando se determinan estas
cantidades experimentalmente.
De estas dos expresiones se obtienen también las relaciones
C pmolar l + 2
molar
molar
C p − CV
γ ≡ molar =
= R,
.
(14)
CV
l
Balance de energía en los procesos de un gas ideal.
a) Proceso isobárico ( p = cte. )
Consideremos el caso en que un gas ideal está contenido en un cilindro como el de la
figura, con un émbolo móvil en su parte superior. Se entrega lentamente cierta cantidad
de calor Q al gas, mediante una fuente de calor en la base del cilindro, y se observa que
el volumen del gas cambia desde un valor V0 al comenzar el proceso, hasta otro valor
V1 al finalizar la entrega de calor. El émbolo está sometido a la carga constante de una
pesa, y el proceso es muy lento, de modo que podemos suponer que durante el mismo la
presión del gas se mantiene constante en un valor p = p0 . También hemos representado
en la figura el proceso en un diagrama de p en función de V .
El trabajo W realizado sobre el gas por el émbolo es
V1
W = − ∫ p dV = − p0 (V1 − V0 ) .
V0
Notemos que si el volumen aumenta el trabajo resulta negativo.
El calor Q entregado al gas se puede escribir en la forma
6
1
T1
0
T0
Q = ∫ δQ = ∫ n C pmolar dT = n C pmolar (T1 − T0 ) =
p
⎛pV pV ⎞
⎛l
⎞
= n C pmolar ⎜ 0 1 − 0 0 ⎟ = C pmolar 0 (V1 − V0 ) = ⎜ + 1⎟ p0 (V1 − V0 ).
nR ⎠
R
⎝2 ⎠
⎝ nR
Para la variación ΔU de energía interna obtenemos
l
ΔU = Q + W = p0 (V1 − V0 )
2
b) Proceso isocórico ( V = cte. )
Consideremos ahora el gas contenido en un cilindro cerrado, como el que se indica en la
figura siguiente, con un volumen V0 fijo. Se le entrega lentamente al gas una cantidad
de calor Q . También se representa en la figura el proceso en un diagrama de p en
función de V , donde se puede observar que la presión cambia desde un valor inicial p0
hasta un valor p1 .
En este caso el trabajo W sobre el gas es cero porque no hay variación de volumen
V1
V0
V0
V0
W = − ∫ p dV = − ∫ p dV = 0.
El calor Q entregado al gas se obtiene de la siguiente forma
1
Q = ∫ δQ =
0
T1
∫nC
molar
V
dT = n C Vmolar (T1 − T0 ) =
T0
pV ⎞
V
l
⎛ pV
= n C Vmolar ⎜ 1 0 − 0 0 ⎟ = C Vmolar 0 ( p1 − p 0 ) = V 0 ( p1 − p 0 ),
nR ⎠
R
2
⎝ nR
y la variación de energía interna resulta
l
ΔU = Q + W = V0 ( p1 − p0 ) .
2
c) Proceso isotérmico ( T = cte. )
Consideremos ahora nuevamente al gas en un cilindro con un embolo movil, que se
mueve lentamente de modo que el volumen cambie desde un valor V0 hasta otro valor
V1 . El proceso se realiza manteniendo el gas en contacto térmico con un gran sistema
con temperatura constante T0 , de modo que podemos considerar que gas tiene durante
7
todo el proceso la misma temperatura T0 . El proceso se ilustra en la figura siguiente,
donde también se ha representado la evolución isotérmica del gas como una porción de
la hipérbola p (V ) = nRT0 / V en un diagrama de p en función de V .
El trabajo que hace el émbolo sobre el gas resulta
V1
V1
⎛V ⎞
1
dV = − nRT0 ln⎜⎜ 1 ⎟⎟
V
⎝ V0 ⎠
V0
W = − ∫ p(V ) dV = − nRT0 ∫
V0
Destaquemos que si el volumen aumenta ( V1 > V0 ), la expresión anterior determina un
trabajo negativo (que sale del gas), mientras que si el volumen disminuye ( V1 < V0 ), el
gas recibe trabajo del émbolo, y W > 0 .
Sabemos que para el gas ideal, la energía interna depende solamente de la temperatura
( U = nlRT / 2 = U (T ) ), de modo que la energía interna no cambia en este proceso
isotérmico
ΔU = 0
Usando los resultados obtenidos para W y ΔU , en la expresión del primer principio
ΔU = Q + W , se obtiene también
⎛V ⎞
Q = −W = nRT0 ln⎜⎜ 1 ⎟⎟
⎝ V0 ⎠
Si el volumen aumenta, vemos que Q > 0 (entra calor al gas desde el foco térmico). En
cambio, si el volumen disminuye resulta Q < 0 .
d) Proceso adiabático ( Q = 0 )
Consideraremos ahora el caso en que el gas está encerrado en un cilindro que tiene un
émbolo móvil en su parte superior, para el caso en que. El émbolo se desplaza de modo
que el volumen inicial del gas es V0 , y el volumen al final del proceso es V1 .
Supondremos que las paredes del cilindro y el émbolo son muy malos conductores del
calor, de modo que en este proceso no entra ni sale energía en forma de calor, es decir
que
Q = 0.
En la figura siguiente se representa esquemáticamente este proceso. El rayado en las
paredes del cilindro y en el émbolo designan su carácter adiabático.
8
Si intentamos calcular el trabajo que el émbolo hace sobre el gas debemos evaluar la
V1
integral W = − ∫ p dV , y para ello debemos conocer como es la presión en función del
V0
volumen durante el proceso adiabático. Veamos entonces como determinar p = p(V ) .
Para un proceso infinitesimal reversible el primer principio de la termodinámica se
escribe en la forma dU = δQ − pdV . Si el proceso es adiabático resulta δQ = 0 , y
entonces
dU = − pdV
Por otro lado, si consideramos a la energía interna como función de las variables p y
V ( U = U ( p,V ) ), resulta también
⎛ ∂U ⎞
⎛ ∂U ⎞
⎟⎟ dp + ⎜
dU = ⎜⎜
⎟ dV
⎝ ∂V ⎠ p
⎝ ∂p ⎠V
Igualando las dos últimas ecuaciones se obtiene
⎡⎛ ∂U ⎞
⎤
⎛ ∂U ⎞
⎜⎜
⎟⎟ dp + ⎢⎜
(15)
⎟ + p ⎥ dV = 0
⎢⎣⎝ ∂V ⎠ p
⎥⎦
⎝ ∂p ⎠V
Esta última ecuación estable una relación que vincula una pequeña variación dp de la
presión con la correspondiente pequeña variación del volumen dV , para una evolución
adiabática infinitesimal. ¡Ya estamos más cerca de obtener la presión en función del
volumen!.
Para calcular las derivadas parciales en la última ecuación, necesitamos expresar la la
energía interna del gas ideal como función de la presión y el volumen. Esto se logra
reemplazando en U = nlRT / 2 la ecuación de estado pV = nRT . Se obtiene entonces
l
l
U = nRT = pV = U ( p,V ) ,
2
2
y las siguientes derivadas parciales
⎛ ∂U ⎞
l
l
⎛ ∂U ⎞
⎜⎜
⎟⎟ = V ,
⎟ = p.
⎜
⎝ ∂V ⎠ p 2
⎝ ∂p ⎠V 2
Con estas derivadas parciales reemplazadas en la ecuación (15) se obtiene
9
molar
dp
dV
l + 2 Cp
γ=
= −γ
,
= molar .
p
V
l
CV
Integrando esta última expresión entre el estado inicial ( p0 ,V0 ) y un estado ( p,V ) que
pertenezca a la evolución adiabática se obtiene
p
( p ,V )
( p ,V )
V
⎛ p⎞
⎛V ⎞
dp
dV
dp
dV
= −γ ∫
= −γ ∫
,
,
ln⎜⎜ ⎟⎟ = −γ ln⎜⎜ ⎟⎟ .
∫
∫
p
V
p
V
⎝ p0 ⎠
⎝ V0 ⎠
p0
V
( p 0 ,V0 )
( p 0 ,V0 )
De esta última ecuación resulta
pV γ = p0V0γ = cte.
¡Por fin!, esta es la ecuación que buscábamos, y que relaciona la presión y el volumen
para un gas ideal en una evolución adiabática. En la siguiente figura se representa el
proceso adiabático en un diagrama de la presión en función del volumen
Ahora podemos calcular el trabajo sobre el gas:
V1
V1
1− γ
1
γ V
W = − ∫ p(V ) dV = − p0V0 ∫ γ dV = − p0V0
V
1− γ
V0
V0
γ
V1
=
V0
1
(pV − p V ).
γ −1 1 1 0 0
La variación de energía interna resulta
ΔU = W + Q = W =
10
1
( p V − p0V0 ) .
γ −1 1 1
El motor de cuatro tiempos.
Los motores de autos, ómnibus y camiones son ejemplos de máquinas térmicas.
La producción de movimiento en los motores comienza por el quemado de combustible
en su interior.
En los motores a nafta el quemado se produce en la cámara de combustión, que está
formada por un cilindro con dos válvulas (una de admisión y otra de escape) y una
bujía de encendido (los motores diesel no tienen bujía de encendido). La válvula de
admisión permite la entrada de la mezcla de aire y combustible al cilindro, y la válvula
de escape permite la salida de los gases resultantes de la combustión. El pistón se
acopla por medio de la biela al cigüeñal. El cierre y la abertura de las válvulas es
controlado externamente por un sistema acoplado al cigüeñal.
11
Como resultado de la combustión, hay un movimiento de vaivén del pistón. Debido al
acoplamiento entre pistón, biela y cigüeñal, este movimiento de vaivén es convertido
hacia fuera del motor en un movimiento de rotación.
Veamos como funciona un motor de combustión interna.
El proceso comienza cuando la mezcla de aire y aire y combustible entra al cilindro por
la válvula de admisión. A medida que el pistón desciende, la mezcla es aspirada y
llenando el volumen del cilindro. Durante esa parte del proceso la válvula de escape
permanece cerrada, como se indica en la figura 2.4.
Cuando el pistón vuelve a subir, debido a la inercia del cigüeñal, la mezcla queda
confinada en un volumen cada vez menor, aumentando su presión y su temperatura. En
esta parte del proceso las dos válvulas permanecen cerradas. La figura 2.5 muestra la
compresión de la mezcla.
En el punto de máxima compresión de la mezcla, la bujía produce una chispa que
provoca una combustión muy rápida (explosión), produciendo un gran calentamiento de
los gases resultantes, y un gran aumento de la presión en el interior del cilindro.
Debido a la rapidez de la explosión y a la inercia del sistema, el descenso del pistón
ocurre después de la explosión. Las válvulas siguen cerradas durante esta parte del
proceso, en que el pistón desciende hasta ocupar la posición más baja. La figura 2.6
ilustra esta parte del proceso.
12
Finalmente, para el volumen máximo del cilindro, la válvula de escape se abre, y una
parte de los gases es liberada muy rápidamente, debido a la baja presión exterior. A
continuación, el pistón sube debido a la inercia del cigüeñal, eliminando el resto de los
gases de combustión. Esta disminución de volumen del cilindro ocurre a presión
constante. Esta parte del proceso se indica en la figura 2.7.
13
Después se cierra la válvula de escape, se abre la admisión y todo el proceso se repite.
A continuación se resumen las distintas etapas de funcionamiento del motor, con los
procesos involucrados, y se representa gráficamente las variaciones de presión y
volumen.
1a. etapa: admisión de la mezcla
Con la válvula de admisión abierta, aumenta el volumen la presión mientras la presión
permanece prácticamente constante (A→B)
2a. etapa: compresión de la mezcla
Mientras el volumen disminuye, la presión y la temperatura aumentan (B→C)
3a. etapa: explosión de la mezcla
Al principio el volumen permanece prácticamente constante y la presión aumenta
(C→D), después el volumen aumenta mientras la presión y la temperatura disminuyen
(D→E).
14
4a. etapa: escape de los gases
Se abre la válvula de escape y disminuye la presión a volumen constante (E→B), y
después el volumen disminuye con presión prácticamente constante (B→A).
Todos estos procesos pueden ser representados en el único diagrama presión-volumen
dec la figura 2.8, para un ciclo completo del motor de combustión interna, que se
denomina ciclo Otto.
En este diagrama podemos identificar las distintas transformaciones que ocurren en un
ciclo del motor.
En el tramo A→B, la velocidad con que ingresa la mezcla es impuesta por la velocidad
del pistón, haciendo que la presión permanezca constante. Por eso este proceso se
denomina isobárico.
En el tramo B→C, todo el trabajo que realiza el pistón se convierte en energía interna
de la mezcla, con aumento de la presión y de la temperatura. Esto es una compresión
15
adiabática, o sea sin intercambio de calor con el exterior, ya que el proceso es muy
rápido.
En el tramo C→D ocurre la explosión, que por ser muy rápida no da tiempo suficiente
para el movimiento del pistón, y por lo tanto, para la variación del volumen. La energía
del combustible es entonces convertida en energía interna, con una gran elevación de la
temperatura de los gases que resultan de la reacción. Entonces esa transformación puede
considerarse isocórica.
En el proceso D→E, la segunda parte de la etapa de explosión, el pistón desciende tan
rápido que no hay tiempo para intercambiar calor. Por eso la expansión también se
considera adiabática.
En el proceso E→B, la abertura de la válvula de escape hace que ocurra una variación
de masa y de presión de la mezcla, sin que haya tiempo para que el pistón cambie de
posición, y por lo tanto de volumen. Esa descompresión puede considerarse isocórica.
En el tramo B→A ocurre la expulsión de los productos de la explosión. La masa de gas
contenido en el cilindro disminuye en la misma proporción en que lo hace el volumen, y
el proceso puede considerarse isobárico.
Los vehículos tienen en general varios cilindros con sus pistones conectados al mismo
cigüeñal.
La descripción que hemos hecho de las transformaciones que ocurren en un ciclo
completo de un pistón, son solo aproximadas. El diagrama de las verdaderas variaciones
de presión y de volumen en un motor presenta algunas diferencias respecto del análisis
anterior. Así, la admisión no es perfectamente isobárica, porque el ingreso de la mezcla
no acompaña exactamente el movimiento del pistón, lo que ocasiona una caída de la
presión. La explosión tampoco es perfectamente isocórica, porque no es instantánea, y
ocurre mientras el pistón se mueve. El escape isocórico no es tal, porque el pistón
invierte rápidamente su velocidad y comienza a empujar los gases hacia fuera. El escape
real tampoco es isobárico porque el pistón tiene una velocidad mayor que la de salida
del gas.
Para un ciclo completo de un motor real, el diagrama presión-volumen tiene la siguiente
forma
Trabajo realizado por el motor.
Aunque haya cuatro etapas del funcionamiento en un ciclo del motor, solo en la tercera
etapa el motor realiza trabajo, porque es cuando los gases resultantes de la explosión
empujan el pistón
En las otras tres etapas (admisión, compresión y escape), la continuidad del movimiento
del pistón se da a través de un trabajo externo, debido a la inercia del conjunto al que
16
están acoplados los pistones con el cigüeñal. Además, la temperatura de los gases que
salen por el escape durante la cuarta etapa es más alta que la temperatura antes de la
explosión. Eso significa que parte del calor de combustión es eliminado en forma de
energía interna de los gases, y también como flujo de calor desde el cuerpo del motor al
ambiente.
La parte restante del calor de combustión se convierte en energía de movimiento del
pistón (realización de trabajo), cerrando de esta forma el balance energético.
Considerando que en un ciclo de funcionamiento de un motor la energía del
combustible es consumida totalmente, en parte realizando un trabajo, y en parte siendo
transferida al medio exterior, podemos afirmar que ese motor, para realizar un nuevo
ciclo, debe recibir una nueva cantidad de combustible (energía).
Rendimiento.
Un indicador importante de cómo funciona un motor es su rendimiento η , que se
expresa como el cociente entre el trabajo neto W que es capaz de entregar y la cantidad
de energía que consume Q:
W
η=
Q
Como el funcionamiento se repite en cada ciclo, basta con que consideremos el
rendimiento en un ciclo. Vamos a tratar de calcular ese rendimiento para el ciclo ideal
descripto anteriormente, en donde además supondremos que la mezcla en el cilindro se
comporta como un gas ideal.
Son muchas idealizaciones, así que no podemos esperar que nuestros cálculos nos
provean de una expresión para el rendimiento muy confiable, pero esperamos que al
menos nos de cierta información aproximada de los factores que influyen en el
rendimiento de un motor.
La energía Q que consume el motor en un ciclo es el calor generado por la explosión en
el tramo C→D, en el que n moles de gas se expanden a volumen constante. Tenemos
entonces que
Q = n CV (TD − TC ) ,
donde CV es el calor molar a volumen constante del gas, mientras que TC y TD son las
temperaturas del gas dentro del cilindro en los estados que se representan con los puntos
C y D en el diagrama presión-volumen.
Se pierde energía en el proceso E→B→A→B, en el que n moles de gas resultante de la
combustión, a la temperatura TE, es reemplazado por la misma cantidad de moles de
mezcla combustible proveniente del carburador, a la temperatura menor TB. La pérdida
de energía es
ΔU = n CV TE − n CV TB .
Podemos escribir entonces
ΔU
Q − ΔU
T −T
η=
=1−
=1− E B .
Q
Q
TD − TC
B
Recordemos que, en un proceso adiabático, la expresión TV γ −1 se mantiene constante.
Los procesos B→C y D→E son adiabáticos, de modo que se cumplen las igualdades
γ −1
γ −1
γ −1
γ −1
TBVmax
= TCVmin
, TEVmax
= TDVmin
,
donde Vmax y Vmin son los volúmenes máximo y mínimo de gas que puede encerrar el
pistón dentro del cilindro. El cociente r = Vmax Vmin se denomina relación de
compresión del motor.
De las últimas igualdades se obtiene entonces
17
TC = TB r γ −1 , TD = TE r γ −1 .
Reemplazando ahora estas expresiones de TC y TD en la expresión del rendimiento η
resulta
1
η = 1 − γ −1 .
r
Según esta última expresión, el rendimiento es siempre menor que uno, aun para este
modelo idealizado. Si r=8 y γ=1,4 (el valor para el aire), el rendimiento teórico es 0,56,
o sea el 56%. El rendimiento se puede aumentar aumentando r, pero esto también
aumenta la temperatura al final de la compresión adiabática de la mezcla de aire y
combustible. Si la temperatura es excesiva, la mezcla explota espontáneamente durante
la compresión en lugar de quemarse después de ser encendida por la chispa de la bujía.
Esto se denomina autoencendido, y causa un golpeteo que puede dañar el motor. La
relación de compresión práctica máxima par la nafta de alto octano es de cerca de 10. Se
pueden usar relaciones mayores con combustibles especiales.
El ciclo Otto que hemos descripto, es un modelo muy idealizado: supone que la mezcla
se comporta como un gas ideal, e ignora la fricción, turbulencia, perdidas de calor hacia
las paredes del cilindro y muchos otros efectos que reducen aun más el rendimiento del
motor. Otra fuente de ineficiencia es la combustión incompleta. El calor obtenido de la
nafta es entonces menor que el calor de combustión total, y los gases del escape
contribuyen a la contaminación del aire. Los rendimientos de los motores a nafta reales
suelen ser del 20%.
18